18.2 勾股定理的逆定理课件 (共21张PPT)
文档属性
| 名称 | 18.2 勾股定理的逆定理课件 (共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-26 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
18.2 勾股定理的逆定理
沪科版 八年级下
新知导入
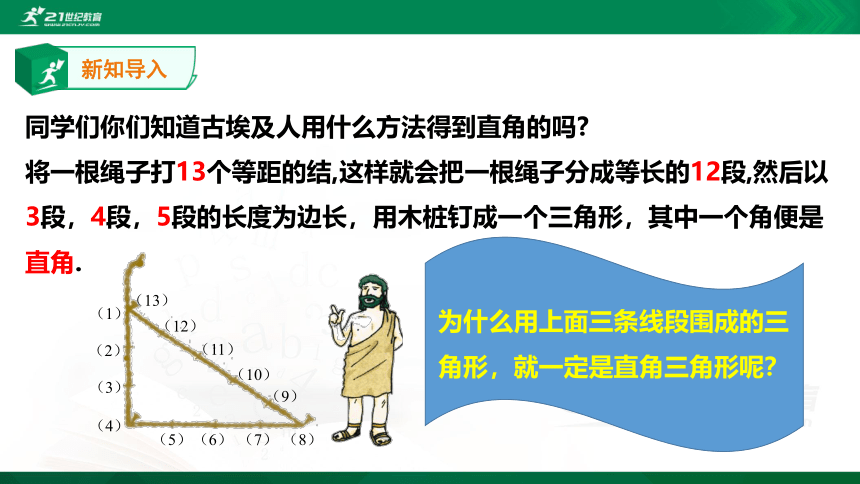
同学们你们知道古埃及人用什么方法得到直角的吗?
将一根绳子打13个等距的结,这样就会把一根绳子分成等长的12段,然后以3段,4段,5段的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.
为什么用上面三条线段围成的三角形,就一定是直角三角形呢?
新知讲解
下面有三组数分别是一个三角形的三边长a, b, c:
①5,12,13; ②7,24,25; ③8,15,17.
问题1 这三组数在数量关系上有什么相同点?
① 5,12,13满足52+122=132,
② 7,24,25满足72+242=252,
③ 8,15,17满足82+152=172.
问题2 古埃及人用来画直角的三边满足这个等式吗?
∵32+42=52,∴满足.
a2+b2=c2
新知讲解
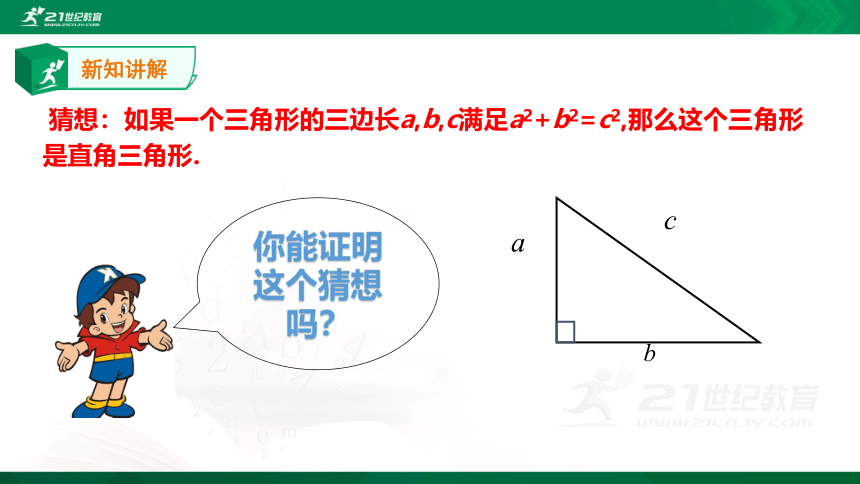
猜想:如果一个三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
新知讲解
已知:如图,△ABC 的三边长a,b,c,满足a2+b2=c2.
求证:△ABC 是直角三角形.
分析:要证△ABC 是直角三角形
∠C 是直角
构造两直角边分别为a,b的Rt△A′B′C′
△ABC ≌ △ A′B′C′
新知讲解
证明:作Rt△A′B′C′,使∠C’=90°,A′C′’=b,B′C ′=a,
则
∴△ABC ≌ △A′B′C′’(SSS),
∴∠C= ∠C′’=90° , 即△ABC 是直角三角形
新知讲解
归纳小结:
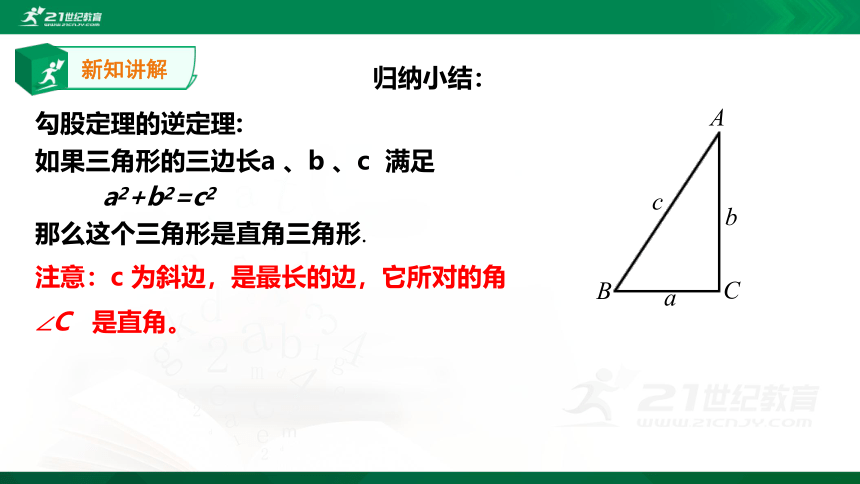
勾股定理的逆定理:
如果三角形的三边长a 、b 、c 满足
a2+b2=c2
那么这个三角形是直角三角形.
注意:c 为斜边,是最长的边,它所对的角
∠C 是直角。
新知讲解
例1 下面以a,b,c 为边长的三角形是不是直角三角形?如果是,那么哪一个角是直角?
(1) a=7 , b=24 ,c=25; (2) a=7 ,b=8 ,c=11.
解:(1)∵72+242=625,252=625,∴72+242=252,
根据勾股定理的逆定理,这个三角形是直角三角形,
且∠C 是直角.
(2)∵72+82=113,112=121,
∴72+82≠112,不符合勾股定理的逆定理,
∴这个三角形不是直角三角形.
新知讲解
例2.已知:在 ?ABC中,三边长分别为a=n2-1,b=2n,c=n2+1(n>1).
求证:?ABC为直角三角形.
证明:∵ a2+b2=(n2-1)2+(2n)2
=n4-2n2+1+4n2
=n4+2n2+1
=(n2+1)2=c2
∴?ABC为直角三角形
能够成为直角三角形三边长度的三个正整数,称勾股数。(如3,4,5)
新知讲解
例3 如图,在正方形ABCD 中,F 是CD 的中点,E 为BC 上一点,且CE= CB,试判断AF 与EF 的位置关系,并说明理由.
解:AF⊥EF.理由如下:
设正方形的边长为4a, 则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,AE2=EF2+AF2,
∴△AEF为直角三角形,且AE为斜边.
∴∠AFE=90°,即AF⊥EF.
课堂练习
1.下列每一组数据中的三个数分别为三角形的三个边长,其中不能构成直角三角形的是( )
A. 3,4,5 B. 6,8,10 C. 5,12,13 D. , 2 ,
2.在Rt△ABC中,若AC2+AB2=BC2,
则 —— =900.
D
∠A
课堂练习
3.下列各组数中,是勾股数的是( )
A. -3,-4,-5 B. 6,8,9 C. 1.5,2,2.5 D. 8 ,15 ,17
点拨:(1)勾股数是正整数;(2)满足a2+b2=c2
4.若△ABC 的三边 a,b,c 满足a2+b2+c2+338=10a+24b+26c. 试判断△ABC 的形状.
点拨:(1)要判断△ABC 的形状,必须推导出a,b,c之间的关系;
(2)本题还需用完全平方公式.
D
课堂练习
解:∵ a2+b2+c2+338=10a+24b+26c,
∴ a2-10a+25+b2-24b+144+c2-26c+169=0.
即 (a-5)?+ (b-12)?+ (c-13)?=0.
∴ a=5, b=12, c=13,
∵52+122=169,132 =169
∴52+122=132
即 a2+b2=c2.
∴△ABC是直角三角形.
拓展提高
5.已知 :如图,四边形ABCD,AB=1,BC = ,CD= ,AD=3,且
AB⊥BC.
求四边形ABCD的面积S.
分析:求一般四边形ABCD的面积,没有
直接公式可求,可转化为两个三角形分别
求之.如图连接AC即可。
拓展提高
解:连接AC,∵AB⊥BC
∴△ABC是直角三角形.
∴AC2=AB2+BC2=12+( )2=
S△ABC= AB*BC= ×1× =
AC2+AD2= +32= CD2=( )2=
∴ AC2+AD2= CD2
∴△ADC是直角三角形,∴ S△ADC= AD*AC= × ×3=
S= S△ABC+S△ADC= + =
中考链接
6.(安庆中考)若一个三角形的三边a,b,c满足
(a+b)(a-b)=c2,那么这个三角形是
———————— 三角形。
点拨:由(a+b)(a-b)=c2
得:a2=b2+c2
∴ 该三角形是以∠A=900的直角三角形.
∠A=900的直角
课堂总结
本节课你有什么收获?
本节课我们主要学习了勾股定理的逆定理:
如果三角形的三边长a 、b 、c 满足
a2+b2=c2
那么这个三角形是直角三角形.
板书设计
18.2勾股定理的逆定理
1.勾股定理的逆定理
2.证明勾股定理的逆定理
3.例1... 例2... 例3...
作业布置
课本 P60 页习题18.2
第1--4题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
18.2 勾股定理的逆定理
沪科版 八年级下
新知导入
同学们你们知道古埃及人用什么方法得到直角的吗?
将一根绳子打13个等距的结,这样就会把一根绳子分成等长的12段,然后以3段,4段,5段的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.
为什么用上面三条线段围成的三角形,就一定是直角三角形呢?
新知讲解
下面有三组数分别是一个三角形的三边长a, b, c:
①5,12,13; ②7,24,25; ③8,15,17.
问题1 这三组数在数量关系上有什么相同点?
① 5,12,13满足52+122=132,
② 7,24,25满足72+242=252,
③ 8,15,17满足82+152=172.
问题2 古埃及人用来画直角的三边满足这个等式吗?
∵32+42=52,∴满足.
a2+b2=c2
新知讲解
猜想:如果一个三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
新知讲解
已知:如图,△ABC 的三边长a,b,c,满足a2+b2=c2.
求证:△ABC 是直角三角形.
分析:要证△ABC 是直角三角形
∠C 是直角
构造两直角边分别为a,b的Rt△A′B′C′
△ABC ≌ △ A′B′C′
新知讲解
证明:作Rt△A′B′C′,使∠C’=90°,A′C′’=b,B′C ′=a,
则
∴△ABC ≌ △A′B′C′’(SSS),
∴∠C= ∠C′’=90° , 即△ABC 是直角三角形
新知讲解
归纳小结:
勾股定理的逆定理:
如果三角形的三边长a 、b 、c 满足
a2+b2=c2
那么这个三角形是直角三角形.
注意:c 为斜边,是最长的边,它所对的角
∠C 是直角。
新知讲解
例1 下面以a,b,c 为边长的三角形是不是直角三角形?如果是,那么哪一个角是直角?
(1) a=7 , b=24 ,c=25; (2) a=7 ,b=8 ,c=11.
解:(1)∵72+242=625,252=625,∴72+242=252,
根据勾股定理的逆定理,这个三角形是直角三角形,
且∠C 是直角.
(2)∵72+82=113,112=121,
∴72+82≠112,不符合勾股定理的逆定理,
∴这个三角形不是直角三角形.
新知讲解
例2.已知:在 ?ABC中,三边长分别为a=n2-1,b=2n,c=n2+1(n>1).
求证:?ABC为直角三角形.
证明:∵ a2+b2=(n2-1)2+(2n)2
=n4-2n2+1+4n2
=n4+2n2+1
=(n2+1)2=c2
∴?ABC为直角三角形
能够成为直角三角形三边长度的三个正整数,称勾股数。(如3,4,5)
新知讲解
例3 如图,在正方形ABCD 中,F 是CD 的中点,E 为BC 上一点,且CE= CB,试判断AF 与EF 的位置关系,并说明理由.
解:AF⊥EF.理由如下:
设正方形的边长为4a, 则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,AE2=EF2+AF2,
∴△AEF为直角三角形,且AE为斜边.
∴∠AFE=90°,即AF⊥EF.
课堂练习
1.下列每一组数据中的三个数分别为三角形的三个边长,其中不能构成直角三角形的是( )
A. 3,4,5 B. 6,8,10 C. 5,12,13 D. , 2 ,
2.在Rt△ABC中,若AC2+AB2=BC2,
则 —— =900.
D
∠A
课堂练习
3.下列各组数中,是勾股数的是( )
A. -3,-4,-5 B. 6,8,9 C. 1.5,2,2.5 D. 8 ,15 ,17
点拨:(1)勾股数是正整数;(2)满足a2+b2=c2
4.若△ABC 的三边 a,b,c 满足a2+b2+c2+338=10a+24b+26c. 试判断△ABC 的形状.
点拨:(1)要判断△ABC 的形状,必须推导出a,b,c之间的关系;
(2)本题还需用完全平方公式.
D
课堂练习
解:∵ a2+b2+c2+338=10a+24b+26c,
∴ a2-10a+25+b2-24b+144+c2-26c+169=0.
即 (a-5)?+ (b-12)?+ (c-13)?=0.
∴ a=5, b=12, c=13,
∵52+122=169,132 =169
∴52+122=132
即 a2+b2=c2.
∴△ABC是直角三角形.
拓展提高
5.已知 :如图,四边形ABCD,AB=1,BC = ,CD= ,AD=3,且
AB⊥BC.
求四边形ABCD的面积S.
分析:求一般四边形ABCD的面积,没有
直接公式可求,可转化为两个三角形分别
求之.如图连接AC即可。
拓展提高
解:连接AC,∵AB⊥BC
∴△ABC是直角三角形.
∴AC2=AB2+BC2=12+( )2=
S△ABC= AB*BC= ×1× =
AC2+AD2= +32= CD2=( )2=
∴ AC2+AD2= CD2
∴△ADC是直角三角形,∴ S△ADC= AD*AC= × ×3=
S= S△ABC+S△ADC= + =
中考链接
6.(安庆中考)若一个三角形的三边a,b,c满足
(a+b)(a-b)=c2,那么这个三角形是
———————— 三角形。
点拨:由(a+b)(a-b)=c2
得:a2=b2+c2
∴ 该三角形是以∠A=900的直角三角形.
∠A=900的直角
课堂总结
本节课你有什么收获?
本节课我们主要学习了勾股定理的逆定理:
如果三角形的三边长a 、b 、c 满足
a2+b2=c2
那么这个三角形是直角三角形.
板书设计
18.2勾股定理的逆定理
1.勾股定理的逆定理
2.证明勾股定理的逆定理
3.例1... 例2... 例3...
作业布置
课本 P60 页习题18.2
第1--4题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
