递归与回溯法
图片预览










文档简介
(共36张PPT)
递归与回溯教案
朱全民
递归
什么是递归?先看大家都熟悉的一个民间故事:从前有座山,山上有座庙,庙里有一个老和尚在给小和尚讲故事,故事里说,从前有座山,山上有座庙,庙里有一个老和尚在给小和尚讲故事,故事里说……。象这样,一个对象部分地由它自己组成,或者是按它自己定义,我们称之为递归。
一个函数、过程、概念或数学结构,如果在其定义或说明内部又直接或间接地出现有其本身的引用,则称它们是递归的或者是递归定义的。在程序设计中,过程或函数直接或者间接调用自己,就被称为递归调用。
递归的概念与应用
递归过程是借助于一个递归工作栈来实现的
问题向一极推进,这一过程叫做递推;
问题逐一解决,最后回到原问题,这一过程叫做回归。
递归的过程正是由递推和回归两个过程组成。
递归的概念与应用
用递归方法编写的问题解决程序具有结构清晰,可读性强等优点,且递归算法的设计比非递归算法的设计往往要容易一些,所以当问题本身是递归定义的,或者问题所涉及到的数据结构是递归定义的,或者是问题的解决方法是递归形式的时候,往往采用递归算法来解决。
递归算法在可计算性理论中占有重要地位,它是算法设计的有力工具,对于拓展编程思路非常有用。就递归算法而言并不涉及高深数学知识,只不过初学者要建立起递归概念不十分容易。
我们先从一个最简单的例子导入。
递归及其实现
用递归算法求 n!
定义:函数 fact( n ) = n!
fact( n-1 ) = ( n-1 )!
则有 fact( n ) = n fact( n-1 )
已知 fact( 1 ) = 1
编写如下递归程序
var
n:integer; t:longint;
function fac(n:integer):longint;
begin
if n=0 then fac:=1
else fac:=n*fac(n-1)
end;
begin
write(‘n=’);readln(n);
t:=fac(n);
writeln(‘n!=’,T);
end.
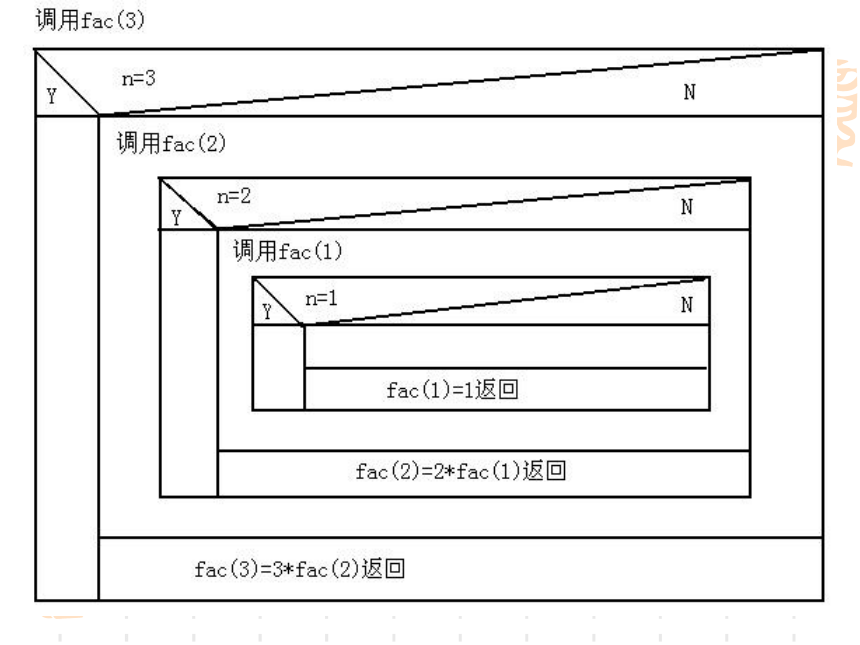
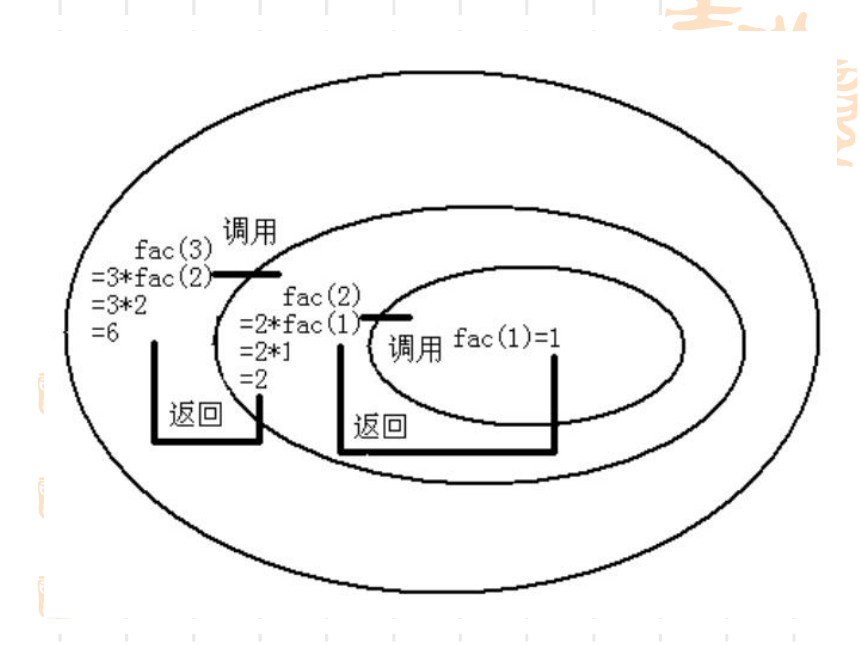
N=3时的递归过程
这相当于从菜心“推到”外层。 递归算法的出发点不放在初始条件上,放在求解的目标上,从所求的未知项出发逐次调用本身的求解过程,直到递归的边界(即初始条件)。就本例而言,读者会认为递归算法可能是多余的,费力而不讨好。但许多实际问题不可能或不容易找到显而易见的递推关系,这时递归算法就表现出了明显的优越性。下面我们将会看到,递归算法比较符合人的思维方式,逻辑性强,可将问题描述得简单扼要,具有良好的可读性,易于理解. 许多看来相当复杂,或难以下手的问题,如果能够使用递归算法就会使问题变得易于处理。
搜索的本质
一、两种题型:
1.简明的数学模型揭示问题本质。对于这一类试题,我们 尽量用解析法求解。
2.对给定的问题建立数学模型,或即使有一定的数学模型,但采用数学方法解决有一定困难。对于这一类试题,我们只好用模拟或搜索求解。
二、搜索的本质:
搜索的本质就是逐步试探,在试探过程中找到问题的
三、搜索问题考察的范围
1.算法的实现能力
2.优化算法的能力
简单回溯法
N皇后问题
背包问题
寻找国都名
……
回溯法
回溯法也是搜索算法中的一种控制策略,但与枚举法不同的是,它是从初始状态出发,运用题目给出的条件、规则,按照深度优秀搜索的顺序扩展所有可能情况,从中找出满足题意要求的解答。回溯法是求解特殊型计数题或较复杂的枚举题中使用频率最高的一种算法。
procedure run(当前状态);
var i:integer;
begin
if 当前状态为边界 then
begin
if 当前状态为最佳目标状态 then 记下最优结果;
exit;{回溯}
end;
for i←算符最小值 to 算符最大值 do
begin
算符i作用于当前状态,扩展出一个子状态;
if (子状态满足约束条件)and(子状态满足最优性要求)then run(子状态)
end;
end;
在应用回溯法求所有路径的算法框架解题时,应考虑如下几个重要因素:
⑴定义状态:即如何描述问题求解过程中每一步的状况。为了精简程序,增加可读性,我们一般将参与子结点扩展运算的变量组合成当前状态列入值参,以便回溯时能恢复递归前的状态,重新计算下一条路径;
⑵边界条件:即在什么情况下程序不再递归下去。如果是求满足某个特定条件的一条最佳路径,则当前状态到达边界时并非一定意味着此时就是最佳目标状态。因此还须增加判别最优目标状态的条件;
⑶搜索范围:在当前状态不满足边界条件的情况下,应如何设计算符值的范围。换句话说,如何设定for语句中循环变量的初值和终值。
⑷约束条件和最优性要求:当前扩展出一个子结点后应满足什么条件方可继续递归下去;如果是求满足某个特定条件的一条最佳路径,那么在扩展出某个子状态后是否继续递归搜索下去,不仅取决于子状态是否满足约束条件,而且还取决于子状态是否满足最优性要求。
⑸参与递归运算的参数:将参与递归运算的参数设为递归子程序的值参或局部变量。若这些参数的存储量大(例如数组)且初始值需由主程序传入,为避免内存溢出,则必须将其设为全局变量,且回溯前需恢复其递归前的值。
N皇后问题
在N*N的棋盘上放置N个皇后而彼此不受攻击(即在棋盘的任一行,任一列和任一对角线上不能放置2个皇后),编程求解所有的摆放方法。
八皇后的两组解
基本思想
由于皇后的摆放位置不能通过某种公式来确定,因此对于每个皇后的摆放位置都要进行试探和纠正,这就是“回溯”的思想。
在N个皇后未放置完成前,摆放第i个皇后和第i+1个皇后的试探方法是相同的,因此完全可以采用递归的方法来处理。
算法基本框架
Procedure Try(I:integer);
{搜索第I行皇后的位置}
var
j:integer;
begin
if I=n+1 then 输出方案;
for j:=1 to n do
if 皇后能放在第I行第J列的位置 then begin
放置第I个皇后;
对放置皇后的位置进行标记;
Try(I+1)
对放置皇后的位置释放标记;
end;
end;
细节处理
怎样判断某列放置了皇后
A:array [1..MaxN] of Boolean;
{竖线被控制标记}
怎样判断某对角线上放置了皇后
B:array [2..MaxN * 2] of Boolean;
{左上到右下斜线被控制标记}
C:array [1–MaxN..MaxN–1] of Boolean;
{左下到右上斜线被控制标记}
0,1背包问题
已知一个容量大小为M重量的背包和N种物品,每种物品的重量为Wi。若将物品放入背包将得到Pi的效益,求怎样选取物品将得到效益最大。
输入
从文件的第一行读入M和N,接下来N行,第i+1行的两个数分别表示第i种物品的重量和效益。
输出
第一行输出一个数,表示背包所装物品的最大效益。
第二行输出若干个数字,分别表示所装物品的标号。
例如,
输入 输出
100 3 180
40 80 1 2
50 100
70 150
算法分析
本题可以用递归求解:设当前有N个物品,容量为M;因为这些物品要么选,要么不选,我们假设选的第一个物品编号为I(1~I-1号物品不选),问题又可以转化为有N-I个物品(即第I+1~N号物品),容量为M-Wi的子问题……如此反复下去,然后在所有可行解中选一个效益最大的便可。
另外,为了优化程序,我们定义一个函数如下:
F[I]表示选第I~N个物品能得到的总效益。不难推出:
F[N]=Pn
F[I]=F[I+1]+Pi (I=1…N-1)
假设当前已选到第I号物品,如果当前搜索的效益值+F[I+1]的值仍然比当前的最优值小,则没有必要继续搜索下去。
算法框架
Procedure Search(I:Integer; J:Byte); {递归求解}
Var K :Byte;
Begin
If Now+F[J]<=Ans Then Exit; {如果没有必要搜索下去}
If Now>Ans Then Begin {修改最优解}
Ans:=Now;
Out:=Ou;
End;
For K:=J To N Do {选取物品}
If W[K]<=I Then Begin
Now:=Now+P[K];
Ou[K]:=True;
Search(I-W[K],K+1);
Now:=Now-P[K];
Ou[K]:=False;
End;
End;
给出一个矩阵及一些国都名:
o k d u b l i n dublin
a l p g o c e v tokyo
r a s m u s m b london
o s l o n d o n rome
y i b l g l r c bonn
k r z u r i c h paris
o a i b x m u z oslo
t p q g l a m v lima
要求从这个矩阵中找出这些国都名,并输出它们的起始位置及方向。
寻找国都名
搜索的方向
算法思想
将字符矩阵读入到二维数组,然后对每一个国都名进行搜索,首先需要在矩阵中找到国都名的第一个字符,然后沿八个方向进行搜索。直到找到国都名为止。若在矩阵中没有找到,则输出相应的信息。
在搜索过程时,类似八皇后问题,建立一个标志数组,标识已经搜索过的方向,在对八个方向搜索时,可以建立一个方向数组,使得程序更加简洁明了
Const
Fx : Array[1..8,1..2] Of Shortint {定义八个方向}
=((0,1),(0,-1),(1,0),(-1,0),(1,-1),(-1,1),(1,1),(-1,-1));
Procedure Work(T,X,Y:Integer);
{搜索路径,T为国都名的字符位置,X,Y为当前搜索的坐标}
Var I : Integer;
Begin
If T=Length(S)+1 Then begin {搜索完,打印输出}
Out; exit end;
For I:=1 To 8 Do {八个方向进行搜索}
Begin
X:=X+Fx[I,1]; Y:=Y+Fx[I,2]; {坐标变化}
If (A[X,Y]=S[T])And(B[X,Y]) Then Begin
W:=W+Chr(I+48); {记录路径}
B[X,Y]:=False; {设置已经搜索}
Work(T+1,X,Y); {继续搜索下一个}
Delete(W,Length(W),1);{恢复原路径}
B[X,Y]:=True; {恢复标志}
End;
X:=X-Fx[I,1]; Y:=Y-Fx[I,2]; {返回后,坐标恢复}
End;
End;
构造字串
生成长度为n的字串,其字符从26个英文字母的前p(p≤26)个字母中选取,使得没有相邻的子序列相等。例如p=3,n=5时
‘a b c b a’满足条件
‘a b c b c’不满足条件
输入:n,p
输出:所有满足条件的字串
分析
状态:待扩展的字母序号at。实际上字串s亦参与了递归运算,但是由于该变量的存储量太大,因此我们将s设为全局变量;
边界条件和目标状态:产生了一个满足条件的字串,即at=n+1;
搜索范围:第at位置可填的字母集{'a'.. chr(ord('a')+p-1)};
约束条件:当前字串没有相邻子串相等的情况
var
n,p:integer;{字串长度和可选字母的个数}
tl:longint; { 满足条件的字串数}
ed:char; { 可选字母集中的最大字母}
s:string; {满足条件的字串}
procedure solve(at:integer);{递归扩展第at个字母}
var
ch:char; i:integer;
begin
if at=n+1 then {若产生了一个满足条件的字串,则输出}
begin
writeln(f,s); inc(tl);exit{回溯}
end;{then}
for ch←'a' to ed do {搜索每一个可填字母}
begin
s←s+ch;i←1;{检查当前字串是否符合条件}
while (i<=at div 2) and
(copy(s,length(s)-i+1,i)<>copy(s,length(s)-2*i+1,i)) do
inc(i);
if i>at div 2 then solve(at+1);
{若当前字串符合条件,则递归扩展下一个字母}
delete(s,length(s),1){恢复填前的字串}
end{for}
end;{solve}
主程序如下:
begin
readln(n,p);
{输入字串长度和前缀长短}
ed←chr(ord(‘a’)+p-1);
{计算可选字母集中的最大字母}
s←‘’; tl←0;
{满足条件的字串初始化为空,字串数为0}
solve(1);
{从第1个字母开始递归计算所有满足条件的字串}
writeln(‘Total:’,tl);
{输出满足条件的字串数}
end.
邮票面值设计
给定一个信封,最多只允许粘贴N张邮票,计算在给定K(N+k<=40) 种邮票的情况下(假定所有的邮票数量都足够),如何设计邮票的面值,能得到最大Max ,使得1-Max之间的每一个邮资值都能得到。
例如,N=3,K=2,如果面值分别为1分、4分,则在l分-6分之间的每一个邮资值都能得到(当然还有8分、9分和12分):如果面值分别为1分、3分,则在1分-7分之间的每一个邮资值都能得到。可以验证当N=3,K=2时,7分就是可以得到连续的邮资最大值,所以Max=7,面值分别为l分、3分。
样例:
Input
N=3 k=2
Output
1 3
Max=7
算法(1)
搜索的过程实质上是枚举K种邮票的面值,然后计算这K种邮票对应的Max值。于是可以得到如下算法:
算法1
Procedure Search(m) 搜索第m种邮票的面值
1. If m = K+1 Then [
2. If 当前方案更优 Then 保存当前方案;
3. Exit;
4. ]
5. For I Am-1+1 to N*Am-1+1 do [
{N*Am-1+1肯定不能有前K中邮票构成}
6. Am := I;
7. Search(m+1);
8. ]
分析
在判断邮资值p是否可用不超过N张邮票贴出时,如果我们贴一张面值为m的邮票,则问题转化为判断邮资值p-m是否可用不超过N-1张邮票贴出。
令S(x)表示贴出邮资值x最少使用的邮票数目,则可以建立如下递推方程:
S(0)=0,
S(x)=min{S(x-Ai)+1|i=1,2,…,K且x>=Ai}。
若S(x)<=N,x=1,2,…,P,当S(p)>N时,则可确定Max=p。
下面我们设计搜索思想:显然一定有面值为1的邮票。可以按递增的次序来搜索各种邮票的面值,关键在于确定每一层搜索的上界。设当前搜索到第i层,用不超过N-1张前i-1种邮票可以得到的Max记为Max(i-1),则第m种邮票面值的上界是Max(i-1)+1,否则邮资值Max(i-1)+1就无法用这m种邮票贴出来了。
优化(算法2)
Procedure Search(m) {搜索第m种邮票的面值}
1. If m = K+1 Then [
2. If 当前方案更优 Then 保存当前方案;
3. Exit;
4. ]
5. For I Am-1+1 to Max(m-1) do [
6. Am := I;
7. Search(m+1);
8. ]
埃及分数
在古埃及,人们使用单位分数的和(形如1/a的, a是自然数)表示一切有理数。如:2/3=1/2+1/6,但不允许2/3=1/3+1/3,因为加数中有相同的。
对于一个分数a/b,表示方法有很多种,但是哪种最好呢?首先,加数少的比加数多的好,其次,加数个数相同的,最小的分数越大越好。
如:
19/45=1/3 + 1/12 + 1/180
19/45=1/3 + 1/15 + 1/45
19/45=1/3 + 1/18 + 1/30,
19/45=1/4 + 1/6 + 1/180
19/45=1/5 + 1/6 + 1/18.
最好的是最后一种,因为1/18比1/180,1/45,1/30,1/180都大。
给出a,b(0输入:a b
输出:若干个数,自小到大排列,依次是单位分数的分母。
例如:
输入:19 45
输出:5 6 18
分析
1.节点类型
是一个K元组(a1,a2,...ak), 代表当前解中的分母a1,a2..ak.
2.节点扩展方法
按照a1但是这个最大值怎么确定呢?
直观的讲,a[k]总不能太大,因为如果a[k]太大,1/a[k]就很小,1/a[k+1],1/a[k+2]就更小,那么,尽管加了很多项,还可能不够a/b.
例如已经扩展到19/45=1/5+
如果第二项是1/100, 那么由于19/45-1/5=2/9=0.22222...
那么接下来至少要0.2222/(1/100)=22项加起来才足够2/9, 所以继续扩展下去至少还要扩展22项,加起来才差不多够a/b。
可变深度的搜索算法
procedure search(k,a,b); {决定第k个分母d[k]}
1. if k=depth+1 then exit {depth需要进行枚举}
2. else if (a =1) and (b>d[k-1]) then [
{a整除b的情况}
3. d[k]:=b;
4. if not found or (d[k]5. ]
6. else [
7. s:=max{ b div a,d[k-1]+1}; {确定d[k]的上下界s,t; }
t:=(depth-k+1)*b div a
8. for i:=s to t do [
9. d[k]:=i;
10. m := gcd(a,b); {a,b的最大公约数为m}
11. search(k+1,(i*a-b) div m,(b*i) div m);
12. ]
13. ]
递归与回溯教案
朱全民
递归
什么是递归?先看大家都熟悉的一个民间故事:从前有座山,山上有座庙,庙里有一个老和尚在给小和尚讲故事,故事里说,从前有座山,山上有座庙,庙里有一个老和尚在给小和尚讲故事,故事里说……。象这样,一个对象部分地由它自己组成,或者是按它自己定义,我们称之为递归。
一个函数、过程、概念或数学结构,如果在其定义或说明内部又直接或间接地出现有其本身的引用,则称它们是递归的或者是递归定义的。在程序设计中,过程或函数直接或者间接调用自己,就被称为递归调用。
递归的概念与应用
递归过程是借助于一个递归工作栈来实现的
问题向一极推进,这一过程叫做递推;
问题逐一解决,最后回到原问题,这一过程叫做回归。
递归的过程正是由递推和回归两个过程组成。
递归的概念与应用
用递归方法编写的问题解决程序具有结构清晰,可读性强等优点,且递归算法的设计比非递归算法的设计往往要容易一些,所以当问题本身是递归定义的,或者问题所涉及到的数据结构是递归定义的,或者是问题的解决方法是递归形式的时候,往往采用递归算法来解决。
递归算法在可计算性理论中占有重要地位,它是算法设计的有力工具,对于拓展编程思路非常有用。就递归算法而言并不涉及高深数学知识,只不过初学者要建立起递归概念不十分容易。
我们先从一个最简单的例子导入。
递归及其实现
用递归算法求 n!
定义:函数 fact( n ) = n!
fact( n-1 ) = ( n-1 )!
则有 fact( n ) = n fact( n-1 )
已知 fact( 1 ) = 1
编写如下递归程序
var
n:integer; t:longint;
function fac(n:integer):longint;
begin
if n=0 then fac:=1
else fac:=n*fac(n-1)
end;
begin
write(‘n=’);readln(n);
t:=fac(n);
writeln(‘n!=’,T);
end.
N=3时的递归过程
这相当于从菜心“推到”外层。 递归算法的出发点不放在初始条件上,放在求解的目标上,从所求的未知项出发逐次调用本身的求解过程,直到递归的边界(即初始条件)。就本例而言,读者会认为递归算法可能是多余的,费力而不讨好。但许多实际问题不可能或不容易找到显而易见的递推关系,这时递归算法就表现出了明显的优越性。下面我们将会看到,递归算法比较符合人的思维方式,逻辑性强,可将问题描述得简单扼要,具有良好的可读性,易于理解. 许多看来相当复杂,或难以下手的问题,如果能够使用递归算法就会使问题变得易于处理。
搜索的本质
一、两种题型:
1.简明的数学模型揭示问题本质。对于这一类试题,我们 尽量用解析法求解。
2.对给定的问题建立数学模型,或即使有一定的数学模型,但采用数学方法解决有一定困难。对于这一类试题,我们只好用模拟或搜索求解。
二、搜索的本质:
搜索的本质就是逐步试探,在试探过程中找到问题的
三、搜索问题考察的范围
1.算法的实现能力
2.优化算法的能力
简单回溯法
N皇后问题
背包问题
寻找国都名
……
回溯法
回溯法也是搜索算法中的一种控制策略,但与枚举法不同的是,它是从初始状态出发,运用题目给出的条件、规则,按照深度优秀搜索的顺序扩展所有可能情况,从中找出满足题意要求的解答。回溯法是求解特殊型计数题或较复杂的枚举题中使用频率最高的一种算法。
procedure run(当前状态);
var i:integer;
begin
if 当前状态为边界 then
begin
if 当前状态为最佳目标状态 then 记下最优结果;
exit;{回溯}
end;
for i←算符最小值 to 算符最大值 do
begin
算符i作用于当前状态,扩展出一个子状态;
if (子状态满足约束条件)and(子状态满足最优性要求)then run(子状态)
end;
end;
在应用回溯法求所有路径的算法框架解题时,应考虑如下几个重要因素:
⑴定义状态:即如何描述问题求解过程中每一步的状况。为了精简程序,增加可读性,我们一般将参与子结点扩展运算的变量组合成当前状态列入值参,以便回溯时能恢复递归前的状态,重新计算下一条路径;
⑵边界条件:即在什么情况下程序不再递归下去。如果是求满足某个特定条件的一条最佳路径,则当前状态到达边界时并非一定意味着此时就是最佳目标状态。因此还须增加判别最优目标状态的条件;
⑶搜索范围:在当前状态不满足边界条件的情况下,应如何设计算符值的范围。换句话说,如何设定for语句中循环变量的初值和终值。
⑷约束条件和最优性要求:当前扩展出一个子结点后应满足什么条件方可继续递归下去;如果是求满足某个特定条件的一条最佳路径,那么在扩展出某个子状态后是否继续递归搜索下去,不仅取决于子状态是否满足约束条件,而且还取决于子状态是否满足最优性要求。
⑸参与递归运算的参数:将参与递归运算的参数设为递归子程序的值参或局部变量。若这些参数的存储量大(例如数组)且初始值需由主程序传入,为避免内存溢出,则必须将其设为全局变量,且回溯前需恢复其递归前的值。
N皇后问题
在N*N的棋盘上放置N个皇后而彼此不受攻击(即在棋盘的任一行,任一列和任一对角线上不能放置2个皇后),编程求解所有的摆放方法。
八皇后的两组解
基本思想
由于皇后的摆放位置不能通过某种公式来确定,因此对于每个皇后的摆放位置都要进行试探和纠正,这就是“回溯”的思想。
在N个皇后未放置完成前,摆放第i个皇后和第i+1个皇后的试探方法是相同的,因此完全可以采用递归的方法来处理。
算法基本框架
Procedure Try(I:integer);
{搜索第I行皇后的位置}
var
j:integer;
begin
if I=n+1 then 输出方案;
for j:=1 to n do
if 皇后能放在第I行第J列的位置 then begin
放置第I个皇后;
对放置皇后的位置进行标记;
Try(I+1)
对放置皇后的位置释放标记;
end;
end;
细节处理
怎样判断某列放置了皇后
A:array [1..MaxN] of Boolean;
{竖线被控制标记}
怎样判断某对角线上放置了皇后
B:array [2..MaxN * 2] of Boolean;
{左上到右下斜线被控制标记}
C:array [1–MaxN..MaxN–1] of Boolean;
{左下到右上斜线被控制标记}
0,1背包问题
已知一个容量大小为M重量的背包和N种物品,每种物品的重量为Wi。若将物品放入背包将得到Pi的效益,求怎样选取物品将得到效益最大。
输入
从文件的第一行读入M和N,接下来N行,第i+1行的两个数分别表示第i种物品的重量和效益。
输出
第一行输出一个数,表示背包所装物品的最大效益。
第二行输出若干个数字,分别表示所装物品的标号。
例如,
输入 输出
100 3 180
40 80 1 2
50 100
70 150
算法分析
本题可以用递归求解:设当前有N个物品,容量为M;因为这些物品要么选,要么不选,我们假设选的第一个物品编号为I(1~I-1号物品不选),问题又可以转化为有N-I个物品(即第I+1~N号物品),容量为M-Wi的子问题……如此反复下去,然后在所有可行解中选一个效益最大的便可。
另外,为了优化程序,我们定义一个函数如下:
F[I]表示选第I~N个物品能得到的总效益。不难推出:
F[N]=Pn
F[I]=F[I+1]+Pi (I=1…N-1)
假设当前已选到第I号物品,如果当前搜索的效益值+F[I+1]的值仍然比当前的最优值小,则没有必要继续搜索下去。
算法框架
Procedure Search(I:Integer; J:Byte); {递归求解}
Var K :Byte;
Begin
If Now+F[J]<=Ans Then Exit; {如果没有必要搜索下去}
If Now>Ans Then Begin {修改最优解}
Ans:=Now;
Out:=Ou;
End;
For K:=J To N Do {选取物品}
If W[K]<=I Then Begin
Now:=Now+P[K];
Ou[K]:=True;
Search(I-W[K],K+1);
Now:=Now-P[K];
Ou[K]:=False;
End;
End;
给出一个矩阵及一些国都名:
o k d u b l i n dublin
a l p g o c e v tokyo
r a s m u s m b london
o s l o n d o n rome
y i b l g l r c bonn
k r z u r i c h paris
o a i b x m u z oslo
t p q g l a m v lima
要求从这个矩阵中找出这些国都名,并输出它们的起始位置及方向。
寻找国都名
搜索的方向
算法思想
将字符矩阵读入到二维数组,然后对每一个国都名进行搜索,首先需要在矩阵中找到国都名的第一个字符,然后沿八个方向进行搜索。直到找到国都名为止。若在矩阵中没有找到,则输出相应的信息。
在搜索过程时,类似八皇后问题,建立一个标志数组,标识已经搜索过的方向,在对八个方向搜索时,可以建立一个方向数组,使得程序更加简洁明了
Const
Fx : Array[1..8,1..2] Of Shortint {定义八个方向}
=((0,1),(0,-1),(1,0),(-1,0),(1,-1),(-1,1),(1,1),(-1,-1));
Procedure Work(T,X,Y:Integer);
{搜索路径,T为国都名的字符位置,X,Y为当前搜索的坐标}
Var I : Integer;
Begin
If T=Length(S)+1 Then begin {搜索完,打印输出}
Out; exit end;
For I:=1 To 8 Do {八个方向进行搜索}
Begin
X:=X+Fx[I,1]; Y:=Y+Fx[I,2]; {坐标变化}
If (A[X,Y]=S[T])And(B[X,Y]) Then Begin
W:=W+Chr(I+48); {记录路径}
B[X,Y]:=False; {设置已经搜索}
Work(T+1,X,Y); {继续搜索下一个}
Delete(W,Length(W),1);{恢复原路径}
B[X,Y]:=True; {恢复标志}
End;
X:=X-Fx[I,1]; Y:=Y-Fx[I,2]; {返回后,坐标恢复}
End;
End;
构造字串
生成长度为n的字串,其字符从26个英文字母的前p(p≤26)个字母中选取,使得没有相邻的子序列相等。例如p=3,n=5时
‘a b c b a’满足条件
‘a b c b c’不满足条件
输入:n,p
输出:所有满足条件的字串
分析
状态:待扩展的字母序号at。实际上字串s亦参与了递归运算,但是由于该变量的存储量太大,因此我们将s设为全局变量;
边界条件和目标状态:产生了一个满足条件的字串,即at=n+1;
搜索范围:第at位置可填的字母集{'a'.. chr(ord('a')+p-1)};
约束条件:当前字串没有相邻子串相等的情况
var
n,p:integer;{字串长度和可选字母的个数}
tl:longint; { 满足条件的字串数}
ed:char; { 可选字母集中的最大字母}
s:string; {满足条件的字串}
procedure solve(at:integer);{递归扩展第at个字母}
var
ch:char; i:integer;
begin
if at=n+1 then {若产生了一个满足条件的字串,则输出}
begin
writeln(f,s); inc(tl);exit{回溯}
end;{then}
for ch←'a' to ed do {搜索每一个可填字母}
begin
s←s+ch;i←1;{检查当前字串是否符合条件}
while (i<=at div 2) and
(copy(s,length(s)-i+1,i)<>copy(s,length(s)-2*i+1,i)) do
inc(i);
if i>at div 2 then solve(at+1);
{若当前字串符合条件,则递归扩展下一个字母}
delete(s,length(s),1){恢复填前的字串}
end{for}
end;{solve}
主程序如下:
begin
readln(n,p);
{输入字串长度和前缀长短}
ed←chr(ord(‘a’)+p-1);
{计算可选字母集中的最大字母}
s←‘’; tl←0;
{满足条件的字串初始化为空,字串数为0}
solve(1);
{从第1个字母开始递归计算所有满足条件的字串}
writeln(‘Total:’,tl);
{输出满足条件的字串数}
end.
邮票面值设计
给定一个信封,最多只允许粘贴N张邮票,计算在给定K(N+k<=40) 种邮票的情况下(假定所有的邮票数量都足够),如何设计邮票的面值,能得到最大Max ,使得1-Max之间的每一个邮资值都能得到。
例如,N=3,K=2,如果面值分别为1分、4分,则在l分-6分之间的每一个邮资值都能得到(当然还有8分、9分和12分):如果面值分别为1分、3分,则在1分-7分之间的每一个邮资值都能得到。可以验证当N=3,K=2时,7分就是可以得到连续的邮资最大值,所以Max=7,面值分别为l分、3分。
样例:
Input
N=3 k=2
Output
1 3
Max=7
算法(1)
搜索的过程实质上是枚举K种邮票的面值,然后计算这K种邮票对应的Max值。于是可以得到如下算法:
算法1
Procedure Search(m) 搜索第m种邮票的面值
1. If m = K+1 Then [
2. If 当前方案更优 Then 保存当前方案;
3. Exit;
4. ]
5. For I Am-1+1 to N*Am-1+1 do [
{N*Am-1+1肯定不能有前K中邮票构成}
6. Am := I;
7. Search(m+1);
8. ]
分析
在判断邮资值p是否可用不超过N张邮票贴出时,如果我们贴一张面值为m的邮票,则问题转化为判断邮资值p-m是否可用不超过N-1张邮票贴出。
令S(x)表示贴出邮资值x最少使用的邮票数目,则可以建立如下递推方程:
S(0)=0,
S(x)=min{S(x-Ai)+1|i=1,2,…,K且x>=Ai}。
若S(x)<=N,x=1,2,…,P,当S(p)>N时,则可确定Max=p。
下面我们设计搜索思想:显然一定有面值为1的邮票。可以按递增的次序来搜索各种邮票的面值,关键在于确定每一层搜索的上界。设当前搜索到第i层,用不超过N-1张前i-1种邮票可以得到的Max记为Max(i-1),则第m种邮票面值的上界是Max(i-1)+1,否则邮资值Max(i-1)+1就无法用这m种邮票贴出来了。
优化(算法2)
Procedure Search(m) {搜索第m种邮票的面值}
1. If m = K+1 Then [
2. If 当前方案更优 Then 保存当前方案;
3. Exit;
4. ]
5. For I Am-1+1 to Max(m-1) do [
6. Am := I;
7. Search(m+1);
8. ]
埃及分数
在古埃及,人们使用单位分数的和(形如1/a的, a是自然数)表示一切有理数。如:2/3=1/2+1/6,但不允许2/3=1/3+1/3,因为加数中有相同的。
对于一个分数a/b,表示方法有很多种,但是哪种最好呢?首先,加数少的比加数多的好,其次,加数个数相同的,最小的分数越大越好。
如:
19/45=1/3 + 1/12 + 1/180
19/45=1/3 + 1/15 + 1/45
19/45=1/3 + 1/18 + 1/30,
19/45=1/4 + 1/6 + 1/180
19/45=1/5 + 1/6 + 1/18.
最好的是最后一种,因为1/18比1/180,1/45,1/30,1/180都大。
给出a,b(0
输出:若干个数,自小到大排列,依次是单位分数的分母。
例如:
输入:19 45
输出:5 6 18
分析
1.节点类型
是一个K元组(a1,a2,...ak), 代表当前解中的分母a1,a2..ak.
2.节点扩展方法
按照a1
直观的讲,a[k]总不能太大,因为如果a[k]太大,1/a[k]就很小,1/a[k+1],1/a[k+2]就更小,那么,尽管加了很多项,还可能不够a/b.
例如已经扩展到19/45=1/5+
如果第二项是1/100, 那么由于19/45-1/5=2/9=0.22222...
那么接下来至少要0.2222/(1/100)=22项加起来才足够2/9, 所以继续扩展下去至少还要扩展22项,加起来才差不多够a/b。
可变深度的搜索算法
procedure search(k,a,b); {决定第k个分母d[k]}
1. if k=depth+1 then exit {depth需要进行枚举}
2. else if (a =1) and (b>d[k-1]) then [
{a整除b的情况}
3. d[k]:=b;
4. if not found or (d[k]
6. else [
7. s:=max{ b div a,d[k-1]+1}; {确定d[k]的上下界s,t; }
t:=(depth-k+1)*b div a
8. for i:=s to t do [
9. d[k]:=i;
10. m := gcd(a,b); {a,b的最大公约数为m}
11. search(k+1,(i*a-b) div m,(b*i) div m);
12. ]
13. ]
同课章节目录
