回溯法

(共32张PPT)
回溯搜索
回溯是一种模拟人类思维过程的算法思想。它的基本方法是：按照深度优先的顺序向下一层扩展结点；扩展到某一层时，若已无法继续扩展且仍未找到解，则退回到父结点，从父结点的下一个分支开始，按同样的策略继续扩展……，直到找到问题的解或证明无解。
　　在４×４方格的棋盘内，放置四个皇后，使得任意两个皇后不在同一行、同一列、同一条对角线上。请找出所有的摆法。
分析：
如果我们把４*４的棋盘看成是一个平面直角坐标系，那么任意两个皇后在平面上的坐标应同时满足以下三个条件：
　　⑴两个皇后的横坐标(行号)不相等。
　　⑵两个皇后的纵坐标（列号）不相等。
　　⑶两个皇后的横坐标之差的绝对值不等于纵坐标之差的绝对值。
I≠K
X[I] ≠ X[K]
|I-K|≠|X[I]-X[K]|
例1、四皇后问题
我们用数组x[i]来描述四个皇后在棋盘上的状态， x[i] =j表示在第i行的第j列放置了一个皇后。
（演示）
空棋盘
134-
1---
11--
12--
13--
131-
132-
133-
14--
141-
142-
143-
144-
2---
21--
22--
23--
24--
241-
2411
2412
2413
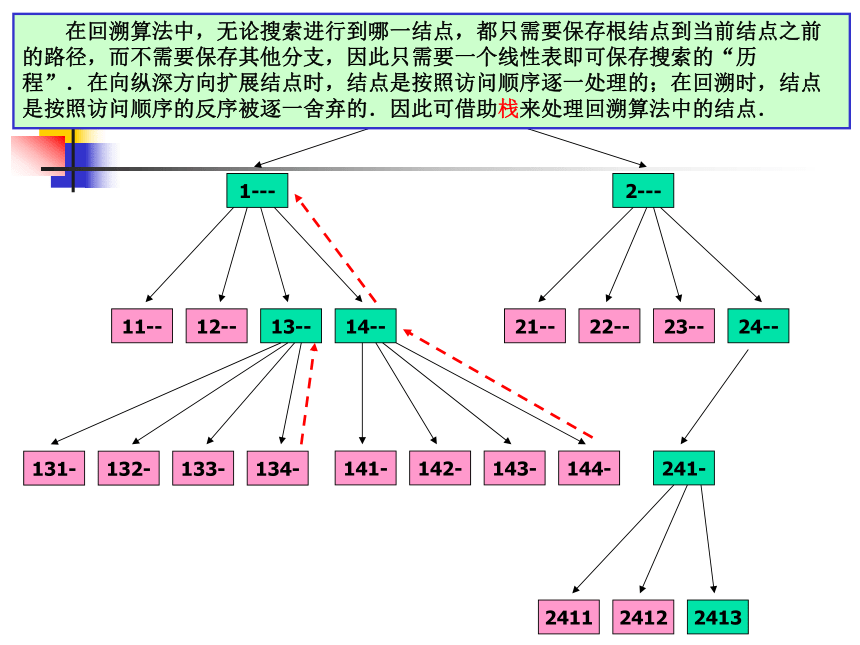
绿色方框表示搜索过程中生成的合法结点，红色方框表示尝试生成的非法结点．
　　在回溯算法中，无论搜索进行到哪一结点，都只需要保存根结点到当前结点之前的路径，而不需要保存其他分支，因此只需要一个线性表即可保存搜索的“历程”．在向纵深方向扩展结点时，结点是按照访问顺序逐一处理的；在回溯时，结点是按照访问顺序的反序被逐一舍弃的．因此可借助栈来处理回溯算法中的结点．
const n=4; var
i,j,k:integer;｛Ｋ是栈顶指针｝
x:array[1..n] of integer;{栈} function place(k:integer):boolean; var i:integer; begin place:=true; for i:=1 to k-1 do if ( )or (abs(x[i]-x[k])=abs(i-k))
then place:=false ; end; procedure print; {输出一种方案} var i:integer; begin for i:=1 to n do write(x[i]:4);
writeln; end;
begin k:=1;｛摆放第一个皇后｝
x[k]:=0;｛保存第k个皇后的列号｝ while ( ) do｛栈非空时｝ begin x[k]:=x[k]+1; while(x[k]<=n)and( ) do
x[k]:=x[k]+1;｛尝试第k行下一列｝ if ( ) then k:=k-1 {回溯} else if k=n then ( ) else begin {摆放下一个皇后}
( );
x[k]:=0
end end ;
end.
x[i]=x[k]
k>0
not place(k)
x[k]>n
print
k:=k+1
不满足约束条件
0
k
1
0
1
2
3
0
1
2
3
4
4
0
1
2
0
1
2
3
4
3
4
2
1
2
3
4
0
1
0
1
2
3
0
例2、数字排列问题
列出所有从数字1到数字n的连续自然数的排列,要求所产生的任一数字序列中不能出现重复的数字．
　　输入：n（1<=n<=9）
　　输出：由1～n组成的所有不重复的数字序列，每行一个序列．
样例
　　输入：
　　３
　　输出：
　　１　２　３
　　１　３　２
　　２　１　３
　　２　３　１
　　３　１　２
　　３　２　１
begin
readln(n);
k:=1;
x[k]:=0;
while k>0 do
begin
x[k]:=x[k]+1;
while ( )
and (not place(k)) do
x[k]:=x[k]+1;
if x[k]>n then( )
else if( )then print
else begin
( );
x[k]:=0
end
end ;
end.
var
i,k,n:integer;｛k是栈顶指针｝
x:array[1..9] of integer;{栈}
function place(k:integer):boolean;
var i:integer;
begin
place:=true;
for i:=1 to k-1 do
if ( )then
begin
place:=false;
break
end ;
end;
procedure print;
var i:integer;
begin
for i:=1 to n do write(x[i],' ');
writeln;
end;
x[k]<=n
x[i]=x[k]
k=n
k:=k+1
k:=k-1
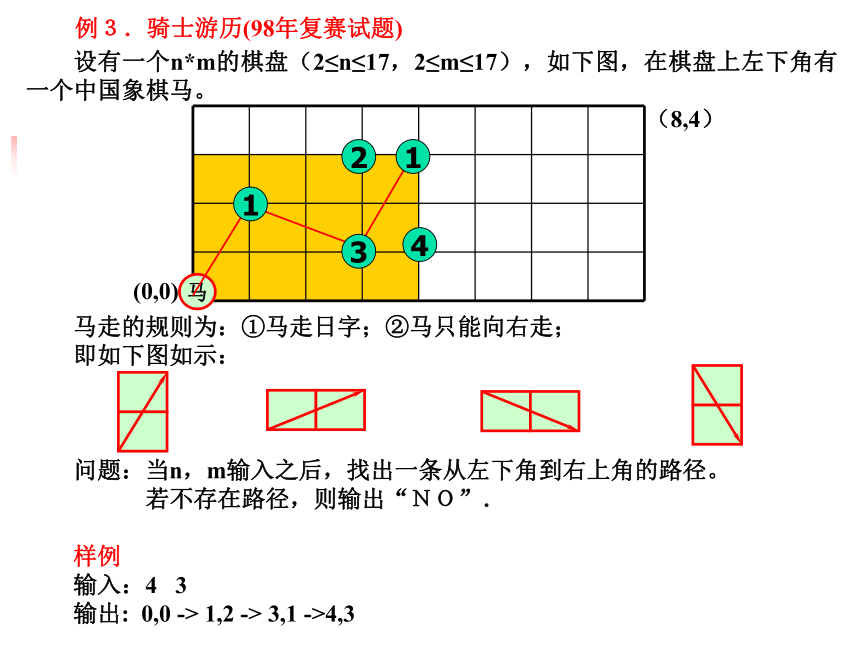
例３．骑士游历(98年复赛试题)
设有一个n*m的棋盘（2≤n≤17，2≤m≤17），如下图，在棋盘上左下角有一个中国象棋马。
（8,4）


(0,0)
马走的规则为：①马走日字；②马只能向右走；
即如下图如示：


问题：当n，m输入之后，找出一条从左下角到右上角的路径。
　　　　　若不存在路径，则输出“ＮＯ”．
样例
输入：4 3
输出: 0,0 -> 1,2 -> 3,1 ->4,3
马
1
2
4
3
1
const
x0:array[1..4]of integer=(1,2,2,1);
y0:array[1..4]of integer=(2,1,-1,-2);
var
m,n,k,i:integer;{k是栈顶指针}
x:array[0..1000,1..2]of integer;{保存每一跳的位置}
y:array[1..1000]of integer;{栈,保存每一跳的方向}
function nok(k:integer):boolean;{会不会出界}
var
i,j:integer;
begin
i:=x[k-1,1]+x0[y[k]];
j:=x[k-1,2]+y0[y[k]];
if(i>n)or(j>m)or(j<0) then nok:=true{出界}
else nok:=false;
end;
begin
readln(n,m);
k:=1; y[k]:=0; x[0,1]:=0; x[0,2]:=0;{起跳点}
while k>0 do
begin
y[k]:=y[k]+1;
while (y[k]<=4)and( ) do y[k]:=y[k]+1;
if y[k]>4 then k:=k-1 {回溯}
else begin
x[k,1]:=x[k-1,1]+x0[y[k]];
x[k,2]:=x[k-1,2]+y0[y[k]];
if( )
then begin
for i:=( )do
write(x[i,1],',',x[i,2],'->');
writeln(n,',',m);
( )
end
else begin
( ) ; y[k]:=0;
end;
end;
end;
writeln('NO');
end.
nok(k)
(x[k,1]=n)and(x[k,2]=m)
0 to k-1
halt
k:=k+1
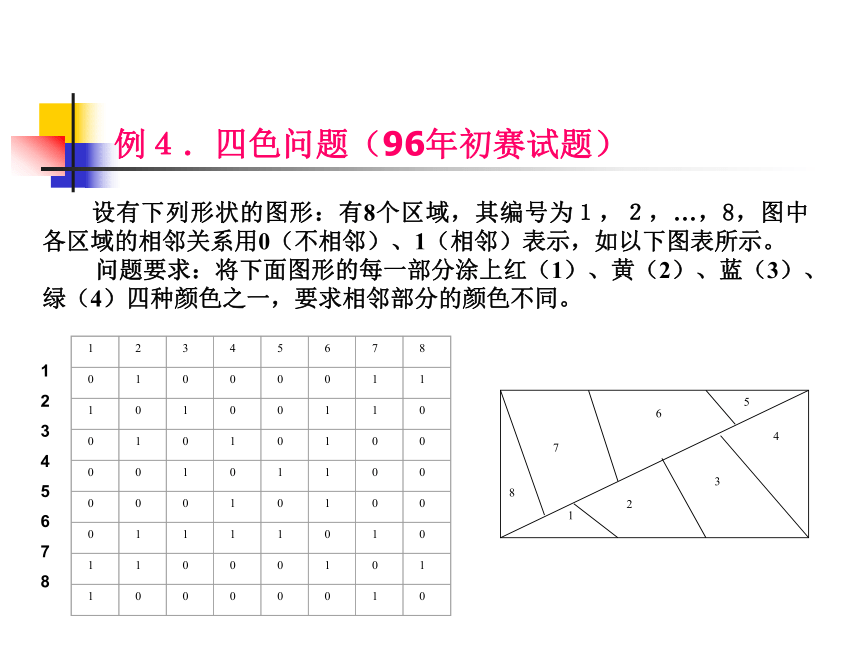
例４．四色问题（96年初赛试题）
8
7
6
5
4
3
2
1
设有下列形状的图形：有8个区域，其编号为１，２，…，8，图中各区域的相邻关系用0（不相邻）、1（相邻）表示，如以下图表所示。
问题要求：将下面图形的每一部分涂上红（1）、黄（2）、蓝（3）、绿（4）四种颜色之一，要求相邻部分的颜色不同。
1
2
3
4
5
6
7
8
0
1
0
0
0
0
1
1
1
0
1
0
0
1
1
0
0
1
0
1
0
1
0
0
0
0
1
0
1
1
0
0
0
0
0
1
0
1
0
0
0
1
1
1
1
0
1
0
1
1
0
0
0
1
0
1
1
0
0
0
0
0
1
0

1
2
3
4
5
6
7
8
分析：设m为图的邻接矩阵。按照涂色的先后顺序将方案存入堆栈s中，其中s[k]为区域k的颜色码，区域k为第k个涂色的区域。在计算过程中，我们必须记住当前涂色的区域号i，该区域称之为栈顶，区域准备涂颜色j（1≤j≤4）。
首先将区域1涂红色（s[1]:=1），并准备涂区域2（i:=2），从颜色1开始试探（j:=1）。区域 i 能否涂颜色j，关键取决于区域 i 的周边是否有同色区域。搜索已涂色的区域1~ 区域i-1中与区域 i 相邻的区域k，看一看这些区域是否涂了颜色j。若与区域 i 相邻的区域 k已经涂了颜色j，按照颜色码递增顺序换一种颜色（j:=j+1）；若区域 i 的周边没有涂颜色 j 的区域，则区域 i 可以涂颜色j（s[i]:=j）。“入栈”，准备涂区域i+1，也从颜色1开始试探（i:=i+1，j:=1）。
对区域i，按照颜色码递增顺序试探颜色。如果区域 i 找不到合适的颜色（j>4）则应该出栈，按照颜色码递增顺序调整区域i-1的颜色（i:=i-1，j:=s[i]+1）。
如此，从区域1出发，依次类推，直至区域n涂好颜色为止（i>n）。
const
　n=8;
var
i,j,k,:integer；{I是栈顶指针}
m:array[1..n，1..n] of 0..1;{图的邻接矩阵}
s:array[1..n] of integer;{栈,存放各区域的颜色}
begin
for i:=1 to n do
begin
for j:=1 to n do read(m[I,j]);readln;
end;
( ); ｛首先给第一个图形涂上红色｝
i:=2; j:=1;
s[1]:=1
while i<=n do
begin
while (j<=4)and(i<=n) do
begin
k:=1；
while( ) do
k:=k+1;
if kelse begin
( );
i:=i+1; j:=1
end
end;
if j>4 then begin
i:=i-1; ( ) ;
end;
end;
(kj)or(r[I,k]<>1))
j:=j+1
S[i]:=j
j:=s[i]+1
for i:=1 to n do writeln(I,’->’,s[i]);
end.
四皇后问题的递归实现
const n=４; var
i,j,k:integer; x:array[1..n] of integer;
{保存第i个皇后的列号} function place(k:integer):boolean; var i:integer; begin place:=true; for i:=1 to k-1 do if(x[i]=x[k])or(abs(x[i]-x[k])=abs(i-k))
then place:=false; end; procedure print; var i:integer; begin for i:=1 to n do write(x[i]:4); writeln; end;
procedure try(k:integer); var i:integer; begin if( ) then
begin
print;
( )
end; for i:=( )do begin ( ); if place(k) then( ); end; end ; begin try(1);{摆放第一个皇后}
end.
k=n+1
x[k]:=i
try(k+1)
1 to n
exit
皇后序号
摆放下一个皇后
因为从第i个皇后到第i+1个皇后的摆放过程是相同的,所以可以用递归的方法.
var
i,k,n:integer;
x:array[1..9] of integer;
function place(k:integer):boolean;
var i:integer;
begin
place:=true;
for i:=1 to k-1 do
if( )then
begin
place:=false;
break
end ;
end;
procedure print;
var i:integer;
begin
for i:=1 to n do write(x[i],' ');
writeln;
end;

数字排列问题的递归实现
x[i]=x[k]
procedure try(k:integer);
var i :integer;
begin
if( )then begin
print;
exit;
end;
for i:=1 to n do
begin
( );
if( )then try(k+1)
end
end;
begin
readln(n);
try(1);
end.
k>n
x[k]:=i
place(k)
骑士游历问题的递归实现
const
x:array[1..4,1..2] of integer
=((1,2),(2,1),(2,-1),(1,-2));
var
n,m:integer;
a:array[1..30,1..2] of integer;
procedure print(ii:integer);
var
i:integer;
begin
for i:=1 to ii-1 do
write(a[i,1],',',a[i,2],'->');
writeln(n,',',m);
( )
end;
procedure try(i:integer);
var
j:integer;
begin
for j:=1 to 4 do
if (a[i-1,1]+x[j,1]<=n)
and (a[i-1,2]+x[j,2]>=0)
and (a[i-1,2]+x[j,2]<=m)
then begin
a[i,1]:=a[i-1,1]+x[j,1];
a[i,2]:=a[i-1,2]+x[j,2];
if (a[i,1]=n)and(a[i,2]=m)
then( )
else( );
( )
end;
end;
begin
read(n,m);
try(2);
writeln(‘NO’);
end.
print(i)
a[i,1]:=0; a[i,2]:=0
try(i+1)
halt

四色问题的递归实现
const
num=20;{最多20个区域}
var
a:array [1..num,1..num] of 0..1;{用邻接矩阵表示图}
s:array [1..num] of 0..4; {1-4代表四色;0代表末填}
i,j,n,k:integer;
function pd(i,j:integer):boolean;{判断可行性}
var
k:integer;
begin
for k:=1 to i-1 do
if (a[i,k]=1) and ( )
then begin
pd:=false; exit;
end;
pd:=true;
end;
j=s[k]
procedure try(i:integer);
var j:integer;
begin
for j:=1 to 4 do
if( )then begin
( );
if i=n then( )
else( );
s[i]:=0;
end;
end;
begin
readln(n);
for i:=1 to n do {读入邻接矩阵}
begin
for j:=1 to n do read(a[i,j]); readln;
end;
for i:=1 to n do s[i]:=0;{初始化}
k:=0;{记数}
try(1);
writeln(k);
end.
pd(i,j)
k:=k+1
s[i]:=j
try(i+1)
二种方式的区别:
1、递归方式实现简单，非递归方式比较复杂。
2、递归方式需要利用栈空间，如果搜索量过大，可能造成栈溢出，所以在栈空间无法满足的情况下，选用非递归方式实现较好。
回溯法的剪枝
　　回溯搜索的进程可以看作是从树根出发，遍历一棵搜索树的过程．所谓剪枝，就是通过某种判断条件，避免一些不必要的遍历过程，形象地说，就是剪去了搜索树中的某些“枝条”．
　　下图是一个求最短路径扩展的搜索树，描述了剪枝的过程．　
A(0)
B(10)
C(20)
D(30)
E(35)
F(40)
G(50)
H(35)
I(25)
J(30)
　　当叶子结点D已找到了一个值为30的最短路径,这时在搜索到G(50)、H(35)、J(30)时，其路径长度已大于或等于了当时最优值，因此再搜索下去毫无意义，其下的结点都可以剪除．
某乡有n个村庄(1输入:村庄数n和各村之间的路程(均是整数)。
输出:最短的路程。
样例输入:
3 {村庄数}
0 2 l {村庄1到各村的路程}
1 0 2 {村庄2到各村的路程}
2 1 0 {村庄3到各村的路程}
样例输出:
3
测试１、售货员的难题
算法分析：
题目给定的村庄数不多(0<40)，所以可以用回溯的方 法，从起点出发找出所有经过其他各村庄的回路，计算其中的最短路程。用一个过程road(step，line：byte)来描述走的状况，其中step是当前已到过的村庄数、line是当前所在的村庄。如果step＝n，接下去只能回起点了，此时看第line个村庄到起点的路程加上已走的总路程，如果它比最小值还小则替换最小值。如果step还小于n，那么将还没有到过的村庄一个一个地试过去，再调用下一步road(step+1，新到的村庄号)。
var
a:array[1..40,1..40] of integer;
n,i,j:integer;
min,m:longint;
bj:array[1..40] of boolean;
begin
readln(n);
for i:=1 to n do
for j:=1 to do read(a[i,j]);
fillchar(bj,sizeof(bj),true);
min:=99999999;
m:=0;
road(1,1);
writeln(min);
end.
procedure road(step,line:byte);
var i,j,k:byte;
begin
if（ ）then
begin
if m+a[line,1]then min:=m+a[line,1];
exit;
end;
for i:=2 to n do
if(i<>line)and（ ）then
begin
m:=m+a[line,i];
bj[line]:=false;
if mthen（ );
m:=m-a[line,i];
（ ）;
end;
end;
step=n
bj[i]
road(step+1,i)
bj[line]:=true
满足最优性要求
优化
恢复其递归前的值
测试2 、棋盘覆盖
有边长为N（偶数）的正方形，用N*N/2个长为2宽为1的长方形将它全部覆盖，请找出所有覆盖方法。如N=4时的一种覆盖方法及输出格式如下所示。
1 2 2 4
1 3 3 4
5 6 6 8
5 7 7 8
输出：
1 2 2 4
1 3 3 4
5 6 6 8
5 7 7 8
var
n:integer;
t:longint;
a:array[1..10,1..10] of integer;
procedure print;
var i,j:integer;
begin
inc(t);
for i:=1 to n do
begin
for j:=1 to n do write(a[i,j]:5);
writeln;
end;
end;
procedure try(i:integer);
var j,k:integer;
begin
j:=0;
repeat{找到第一个未覆盖的空格(j,k)}
j:=j+1; k:=1;
while(k<=n)and(a[j,k]>0) do
inc(k);
until k<=n;
a[j,k]:=i;
if (jbegin
a[j+1,k]:=i;
if i*2else print;
a[j+1,k]:=0;
end;
if (kbegin
a[j,k+1]:=i;
if i*2else print;
a[j,k+1]:=0;
end;
a[j,k]:=0;
end;
begin
readln(n);
try(1);
write(t);
end.
测试3.排队购票
　　公园门票每张5角,如果有2n个人排队购票,每人一张，并且其中一半人恰有５角钱,另一半人恰有１元钱,而票房无零钱可找，那么有多少种方法将这2n个人排成一列，顺次购票，使得不至于因票房无零钱可找而耽误时间？
const maxn=10;
var
a:array[1..maxn*2] of integer;
n,num:integer;
procedure try(k,n0,n1:integer);
var i,j:integer;
begin
if( )then
begin
inc(num);
write('No.',num,' ');
for i:=1 to 2*n do
write(a[i]:2);
writeln;
( );
end;
if(n0=n1)and(n0begin
a[k]:=0;
try( );
end;
　　if( )and(n0　 begin
　 for i:=0 to 1 do
　 begin
　a[k]:=i;
　 if i=0 then try(k+1,n0+1,n1)
　 else try(k+1,n0,n1+1);
　 end;
　end;
　　 if ( )then
　　　 begin
a[k]:=1;
　　　　　try(k+1,n0,n1+1);
end;
end;
begin
　fillchar(a,sizeof(a),0);
　readln(n);
　num:=0;
　try(1,0,0);
end.
k=2*n+1
k+1,n0+1,n1
n0>n1
n0=n
exit
n0是有５角钱的人数n1是有１元钱的人数
测试4.错排问题
在书架上放有编号为1 ，2 ，…，n的n本书。现将n本书全部取下然后再放回去，当放回去时要求每本书都不能放在原来的位置上。
例如：n = 3时：
原来位置为：1 2 3
放回去时只能为：3 1 2 或 2 3 1 这两种
问题：求当n = 5时满足以上条件的放法共有多少种？（不用列出每种放法）
var
a:array[1..50] of integer;
s:set of 1..50;
n,num:integer;
procedure print;
var
i:integer;
begin
inc(num);
write('No.',num,' ');
for i:=1 to n do
write(a[i]:4);
writeln;
end;
procedure cuopai(k:integer);
var
i:integer;
begin
if ( )then begin
print;
exit;
end;
for i:=1 to n do
if not(i in s)and ( ) then
begin
a[k]:=i;
s:=s+[i];
( ) ;
a[k]:=0;
( );
end;
end;
begin
readln(n);
( );
num:=0;
cuopai(1);
writeln('Total=',num);
end.
s:=[]
i<>k
cuopai(k+1)
k=n+1
s:=s-[i]
【问题描述】
棋盘上A点有一个过河卒，需要走到目标B点。卒行走的规则：可以向下、或者向右。同时在棋盘上C点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示，A点(0, 0)、B点(n, m)(n, m为不超过15的整数)，同样马的位置坐标是需要给出的。现在要求你计算出卒从A点能够到达B点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。
【输入】
一行四个数据，分别表示B点坐标和马的坐标。
【输出】
一个数据，表示所有的路径条数。
【样例】
输入:6 6 3 3
输出:6
测试5、马拦过河卒（02年复赛）
const
dx:array[1..8] of integer=(-2,-1,1,2,2,1,-1,-2);
dy:array[1..8] of integer=(1,2,2,1,-1,-2,-2,-1);
var n,m,x,y,i,j: byte;
g:array[0..20,0..20] of 0..1;
c:longint;
procedure sol(x,y:integer);
var i:integer;
begin
if (x=n) and (y=m) then begin
c:=c+1; exit;
end;
if (yif (xend;
begin
readln(n,m,x,y); g[x,y] := 1;
for i:=1 to 8 do
if (x+dx[i]>=0) and (x+dx[i]<=n) and (y+dy[i]>=0) and (y+dy[i]<=m) then
g[x+dx[i],y+dy[i]]:=1;
sol(0,0);
writeln(c);
end.
输入：14 16 7 5
输出：39217645
x,y为当前马所在的位置
描述棋盘上的点是否受马控制
目标
回溯
向右走
向下走
计算马的控制点