人教版九年级数学下册29.2三视图同步练习题含答案
文档属性
| 名称 | 人教版九年级数学下册29.2三视图同步练习题含答案 | 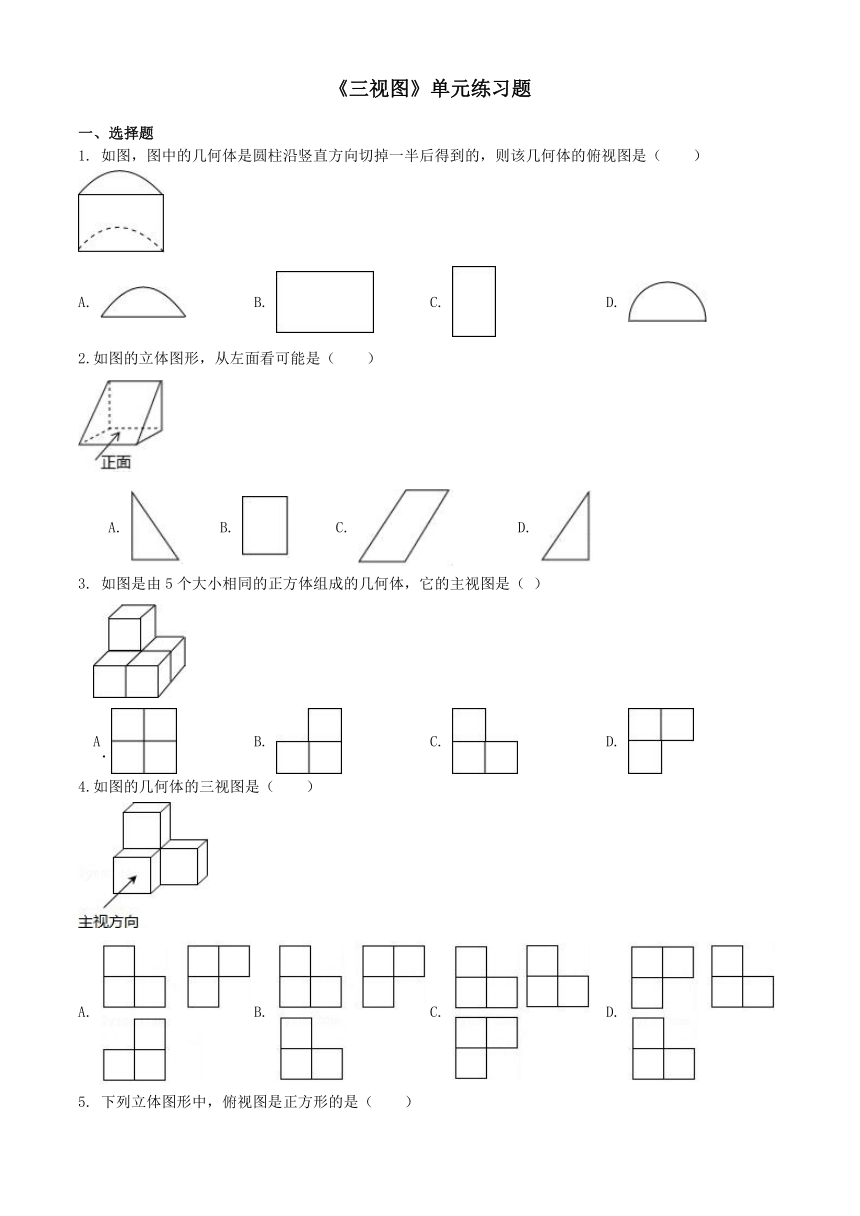 | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-27 09:40:52 | ||
图片预览





文档简介
《三视图》单元练习题
一、选择题
1. 如图,图中的几何体是圆柱沿竖直方向切掉一半后得到的,则该几何体的俯视图是( )
A. B. C. D.
2.如图的立体图形,从左面看可能是( )
A. B. C. D.
3. 如图是由5个大小相同的正方体组成的几何体,它的主视图是( )
A B. C. D.
4.如图的几何体的三视图是( )
A. B. C. D.
5. 下列立体图形中,俯视图是正方形的是( )
A. B. C. D.
6.如图,从左面观察这个立体图形,能得到的平面图形是( ???)
A. B. C. D.
7.如图是由四个相同的小正方形组成的立体图形,它的俯视图为( )
A. B. C. D.
8. 某几何体三视图如图所示,则这个几何体是【 】
A. 圆柱 B. 正方体 C. 球 D. 圆锥
9. 如图所示支架是由两个长方体构成的组合体,则它的主视图是( )
A. B. C. D.
10. 某几何体的三视图如图,则该几何体是( )
A. 三棱柱 B. 长方体 C. 圆柱 D. 圆锥
11.如图是由4个大小相同的正方体搭成的几何体,其俯视图是( )
A. B. C. D.
12. 如图几何体的俯视图是( )
A. B. C. D.
13. 如图的罐头的俯视图大致是( )
A. B. C. D.
14.如图是某个几何体的三视图,则该几何体的形状是( )
A. 长方体 B. 圆锥 C. 圆柱 D. 三棱柱
15.如图,是由几个小立方体所搭成的几何体的俯视图,小正方形中的数字表示在该位置上的立方体的个数,这个几何体的正视图是(?? )
A. B. C. D.
16.左下图是由3个完全相同的小正方体组成的立体图形,它的主视图是( )
A. (A) B. (B) C. (C) D. (D)
17.一个几何体的三视图如图所示,那么这个几何体是( )
A. (A) B. (B) C. (C) D. (D)
18. 如图,所给三视图几何体是( )
A. 球 B. 圆柱 C. 圆锥 D. 三棱锥
19.下列几何体中,有一个几何体的主视图与俯视图的形状不一样,这个几何体是( )
A. 正方体 B. 圆柱 C. 圆锥 D. 球
20.一个几何体的三视图如图所示,则该几何体可能是( )
A. B. C. D.
21.如图是某几何体的三视图,根据图中数据,求得该几何体的体积为( )
A. 60π B. 70π C. 90π D. 160π
22.甲是某零件的直观图,则它的主视图为( )
A. B. C. D.
23.下列几何体,主视图和俯视图都为矩形的是( )
A B. C. D.
24. 一个圆锥的三视图如图所示,则此圆锥的底面积为【 】
A. 30πcm2 B. 25πcm2 C. 50πcm2 D. 100πcm2
二、填空题
25.写出一个在三视图中俯视图与主视图完全相同的几何体
26.如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是 .
27.如图,这是一个长方体的主视图和俯视图,由图示数据(单位:cm)可以得出该长方体的体积是________cm3.
28.三棱柱的三视图如图所示,△EFG中,EF=8cm,EG=12cm,∠EGF=30°,则AB的长为 cm.
29.如图是一个上下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积为 cm2.(结果可保留根号)
30.如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为______cm2
《三视图》单元练习题
一、选择题
1. 如图,图中的几何体是圆柱沿竖直方向切掉一半后得到的,则该几何体的俯视图是( )
A. B. C. D.
【答案】D
【解析】
【分析】
俯视图是从物体上面看所得到的图形.
【详解】从几何体的上面看俯视图是
,
故选D.
2.如图的立体图形,从左面看可能是( )
A. B.
C. D.
【答案】A
【解析】
【分析】
根据三视图的性质即可解题.
【详解】解:根据三视图的概念可知,该立体图形是三棱柱,左视图应为三角形,且直角应该在左下角,
故选A.
【点睛】本题考查了三视图的识别,属于简单题,熟悉三视图的概念是解题关键.
3. 如图是由5个大小相同的正方体组成的几何体,它的主视图是( )
A. B. C. D.
【答案】C
【解析】
A是该几何体俯视图;
B不是该几何体的三视图;
C是该几何体的主视图或左视图;
D不是该几何体的的三视图;
点睛:从正面看到的图是正视图,从上面看到的图形是俯视图,从左面看到的图形是左视图,能看到的线画实线,看不到的线画虚线.
4.如图几何体的三视图是( )
A. B. C. D.
【答案】C
【解析】
主视图是在物体正面从前向后观察物体得到的图形;俯视图是在水平面内从上向下观察物体得到的图形;左视图是在几何体左侧面观察物体得到的图形.题目中几何体从前向后、从左向右观察得到的图形为:下方两个正方形,左上方一个正方形;从上向下观察到的图形为:上方两个正方形,左下方一个正方形.故选C.
5. 下列立体图形中,俯视图是正方形的是( )
A. B. C. D.
【答案】A
【解析】
试题分析:A的俯视图是正方形,故A正确;
B、D的俯视图是圆,故B、D错误;
C的俯视图是三角形,故C错误;
故选A.
考点:三视图
6.如图,从左面观察这个立体图形,能得到的平面图形是( ???)
A. B. C. D.
【答案】A
【解析】
试题分析:从左面看下面一个正方形,上面一个正方形,故选A.
考点:简单组合体的三视图.
7.如图是由四个相同的小正方形组成的立体图形,它的俯视图为( )
A. B. C. D.
【答案】B
【解析】
【分析】
根据俯视图是从上往下看的图形解答即可.
【详解】从上往下看到的图形是:
.
故选B.
【点睛】本题考查三视图的知识,解决此类图的关键是由三视图得到相应的立体图形.从正面看到的图是正视图,从上面看到的图形是俯视图,从左面看到的图形是左视图,能看到的线画实线,被遮挡的线画虚线.
8. 某几何体的三视图如图所示,则这个几何体是【 】
A. 圆柱 B. 正方体 C. 球 D. 圆锥
【答案】D
【解析】
试题分析:由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.
解:根据主视图和左视图为三角形判断出是锥体,根据俯视图是圆形和圆心可判断出这个几何体应该是圆锥,
故选D.
考点:由三视图判断几何体.
9. 如图所示的支架是由两个长方体构成的组合体,则它的主视图是( )
A. B. C. D.
【答案】D
【解析】
试题分析:试题分析:找到从正面看所得到的图形,从几何体的正面看可得此几何体的主视图是三排,左边一排有两层,右边两排各一层.故选D.
考点:简单组合体的三视图.
10. 某几何体的三视图如图,则该几何体是( )
A. 三棱柱 B. 长方体 C. 圆柱 D. 圆锥
【答案】D
【解析】
试题分析:这个几何体的主视图和左视图都是等腰三角形,所以这个几何体为锥体,由俯视图为圆,可得此几何体为圆锥.故答案选D.
考点:几何体的三视图.
11.如图是由4个大小相同的正方体搭成的几何体,其俯视图是( )
A. B. C. D.
【答案】D
【解析】
试题分析:找到从上面看所得到的图形即可. 从上面看可得到一行正方形的个数为3
考点:简单组合体的三视图.
12. 如图几何体的俯视图是( )
A. B. C. D.
【答案】D
【解析】
试题分析:该几何体的俯视图为,
故选D
考点:简单组合体的三视图.
13. 如图的罐头的俯视图大致是( )
A. B. C. D.
【答案】D
【解析】
试题分析:
解:从上往下看易得俯视图为圆.
故选D.
考点:简单几何体的三视图.
14.如图是某个几何体的三视图,则该几何体的形状是( )
A. 长方体 B. 圆锥 C. 圆柱 D. 三棱柱
【答案】D
【解析】
【分析】
由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.
【详解】解:根据主视图和左视图为矩形判断出是柱体,根据俯视图是三角形可判断出这个几何体应该是三棱柱.
故选D.
【点睛】本题考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
15.如图,是由几个小立方体所搭成的几何体的俯视图,小正方形中的数字表示在该位置上的立方体的个数,这个几何体的正视图是(?? )
A. B. C. D.
【答案】D
【解析】
试题分析:由俯视图可知,几个小立方体所搭成的几何体如图所示,
故正视图为,
故选D.
考点:由三视图判断几何体;简单组合体的三视图.
16.左下图是由3个完全相同的小正方体组成的立体图形,它的主视图是( )
A. (A) B. (B) C. (C) D. (D)
【答案】B
【解析】
主视图是从物体的正面看得到的视图,题目中的几何体从正面看到的图形为,故选B.
17.一个几何体的三视图如图所示,那么这个几何体是( )
A. (A) B. (B) C. (C) D. (D)
【答案】D
【解析】
由主视图和左视图可以得到该几何体是圆柱和小圆锥的复合体,由俯视图可以得到小圆锥的底面和圆柱的底面完全重合.故选C.
点睛:本题考查了由三视图判断几何体,解题时不仅要有一定的数学知识,而且还应有一定的生活经验.
18. 如图,所给三视图的几何体是( )
A 球 B. 圆柱 C. 圆锥 D. 三棱锥
【答案】C
【解析】
试题分析:主视图和左视图看到的是一个三角形,可确定为锥体,俯视图看到的是带有圆心的圆,因此可以确定是圆锥
故选C.
考点:三视图
19.下列几何体中,有一个几何体的主视图与俯视图的形状不一样,这个几何体是( )
A. 正方体 B. 圆柱 C. 圆锥 D. 球
【答案】C
【解析】
A.正方体的主视图与俯视图都是正方形,故A选项不符合题意;
B.圆柱的主视图与俯视图是相同的矩形,故B选项不符合题意;
C.圆锥的主视图是三角形,俯视图是带圆心的圆,故C选项符合题意;
D.球的主视图与俯视图都是圆,故D选项不符合题意.
故选C.
20.一个几何体的三视图如图所示,则该几何体可能是( )
A. B. C. D.
【答案】C
【解析】
试题分析:根据几何体的三视图可知该几何体是:圆锥和圆柱的结合体.故选C.
考点:几何体的三视图.
21.如图是某几何体的三视图,根据图中数据,求得该几何体的体积为( )
A. 60π B. 70π C. 90π D. 160π
【答案】B
【解析】
试题分析:由几何体的三视图得,几何体是高为10,外径为8.内径为6的圆筒,
∴该几何体的体积为.
故选B.
考点:由三视图求体积.
22.甲是某零件的直观图,则它的主视图为( )
A B. C. D.
【答案】A
【解析】
【分析】
根据主视图是从正面看得到的视图判定即可.
【详解】∵该几何体从正面看到的图形是:
故选A.
点睛:本题考查了三视图的知识,主视图是从物体的正面看到的视图.
23.下列几何体,主视图和俯视图都为矩形的是( )
A. B. C. D.
【答案】D
【解析】
试题分析:根据主视图和俯视图的概念可知:主视图和俯视图都为矩形的是长方体,
故选D
考点:三视图
24. 一个圆锥的三视图如图所示,则此圆锥的底面积为【 】
A. 30πcm2 B. 25πcm2 C. 50πcm2 D. 100πcm2
【答案】B
【解析】
根据主视图与左视图可以得到:圆锥的底面直径是10cm,利用圆的面积公式即可求解:
根据主视图与左视图可以得到:圆锥的底面直径是10cm,则底面半径是5cm.
则此圆锥的底面积为:π·52=25πcm2.故选B.
二、填空题
25.写出一个在三视图中俯视图与主视图完全相同的几何体
【答案】球或正方体
【解析】
试题分析:球的俯视图与主视图都为圆;正方体的俯视图与主视图都为正方形.
故答案为球或正方体.
考点:三视图
26.如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是 .
【答案】3.
【解析】
试题分析:根据从上面看得到图形是俯视图,可得俯视图,根据矩形的面积公式,可得答案:
从上面看三个正方形组成的矩形,矩形的面积为1×3=3.
考点:简单组合体的三视图.
27.如图,这是一个长方体的主视图和俯视图,由图示数据(单位:cm)可以得出该长方体的体积是________cm3.
【答案】18
【解析】
分析:首先确定该长方体长、宽、高,直接计算其体积即可.
详解:观察其视图知:该长方体的长为3,宽为2,高为3,
故其体积为:3×2×3=18cm3.
故答案为18.
点睛:本题考查了由三视图判断几何体,牢记长方体的体积计算方法是解答本题的关键.
28.三棱柱的三视图如图所示,△EFG中,EF=8cm,EG=12cm,∠EGF=30°,则AB的长为 cm.
【答案】6
【解析】
试题分析:过点E作EQ⊥FG于点Q,
由题意可得出:FQ=AB,
∵EG=12cm,∠EGF=30°,∴EQ=AB=×12=6(cm).
29.如图是一个上下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积为 cm2.(结果可保留根号)
【答案】(75+360).
【解析】
【详解】根据该几何体的三视图知道其是一个六棱柱,
∵其高为12cm,底面半径为5,
∴其侧面积为6×5×12=360cm2
密封纸盒的侧面积为:×5×6×5=75cm2
∴其全面积为:(75+360)cm2.
30.如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为______cm2
【答案】2π
【解析】
根据三视图易得此几何体为圆锥,由题意得底面直径为2,母线长为2,
∴几何体的侧面积为×2×2π=2π.
