2019-2020学年山东省东营市广饶县七年级(上)期末数学试卷(五四学制)含答案
文档属性
| 名称 | 2019-2020学年山东省东营市广饶县七年级(上)期末数学试卷(五四学制)含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 261.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-27 11:42:38 | ||
图片预览

文档简介
2019-2020学年山东省东营市广饶县七年级(上)期末数学试卷(五四学制)
一、选择题:本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.
1.(3分)下列轴对称图形中,对称轴条数最多的是( )
A. B.
C. D.
2.(3分)在﹣3,﹣(﹣),0,3.14,10%,0.,π,0.1010001000001…(相邻两个1之间0的个数逐次加2)中,有理数的个数为( )
A.4个 B.5个 C.6个 D.7个
3.(3分)如果|3﹣a|+(b+5)2=0,那么点A(a,b)在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
4.(3分)下列运算中:①=±;②=±7;③=﹣=﹣;④()3=9;错误的有( )
A.1个 B.2个 C.3个 D.4个
5.(3分)若一次函数y=kx+b的图象如图所示,则k、b的取值范围是( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
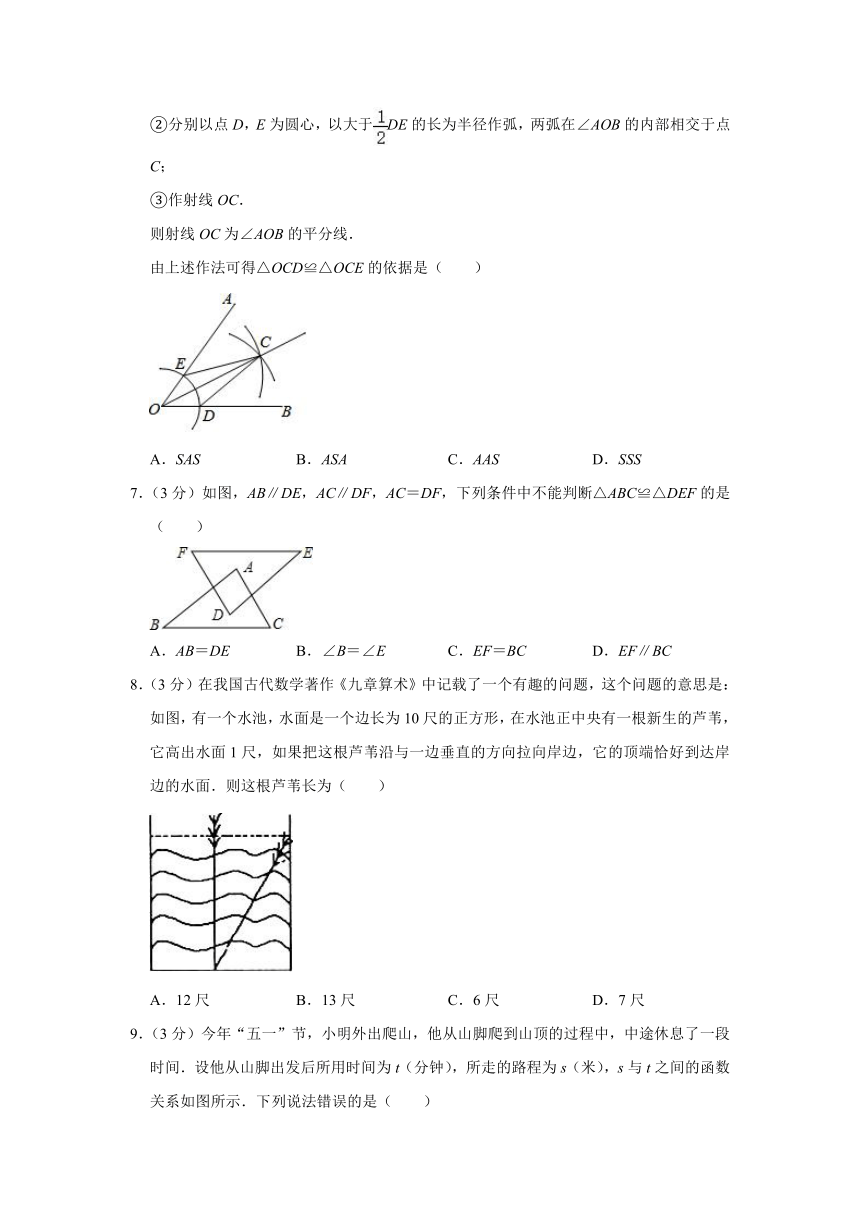
6.(3分)用尺规作图法作已知角∠AOB的平分线的步骤如下:
①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;
②分别以点D,E为圆心,以大于DE的长为半径作弧,两弧在∠AOB的内部相交于点C;
③作射线OC.
则射线OC为∠AOB的平分线.
由上述作法可得△OCD≌△OCE的依据是( )
A.SAS B.ASA C.AAS D.SSS
7.(3分)如图,AB∥DE,AC∥DF,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )
A.AB=DE B.∠B=∠E C.EF=BC D.EF∥BC
8.(3分)在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇沿与一边垂直的方向拉向岸边,它的顶端恰好到达岸边的水面.则这根芦苇长为( )
A.12尺 B.13尺 C.6尺 D.7尺
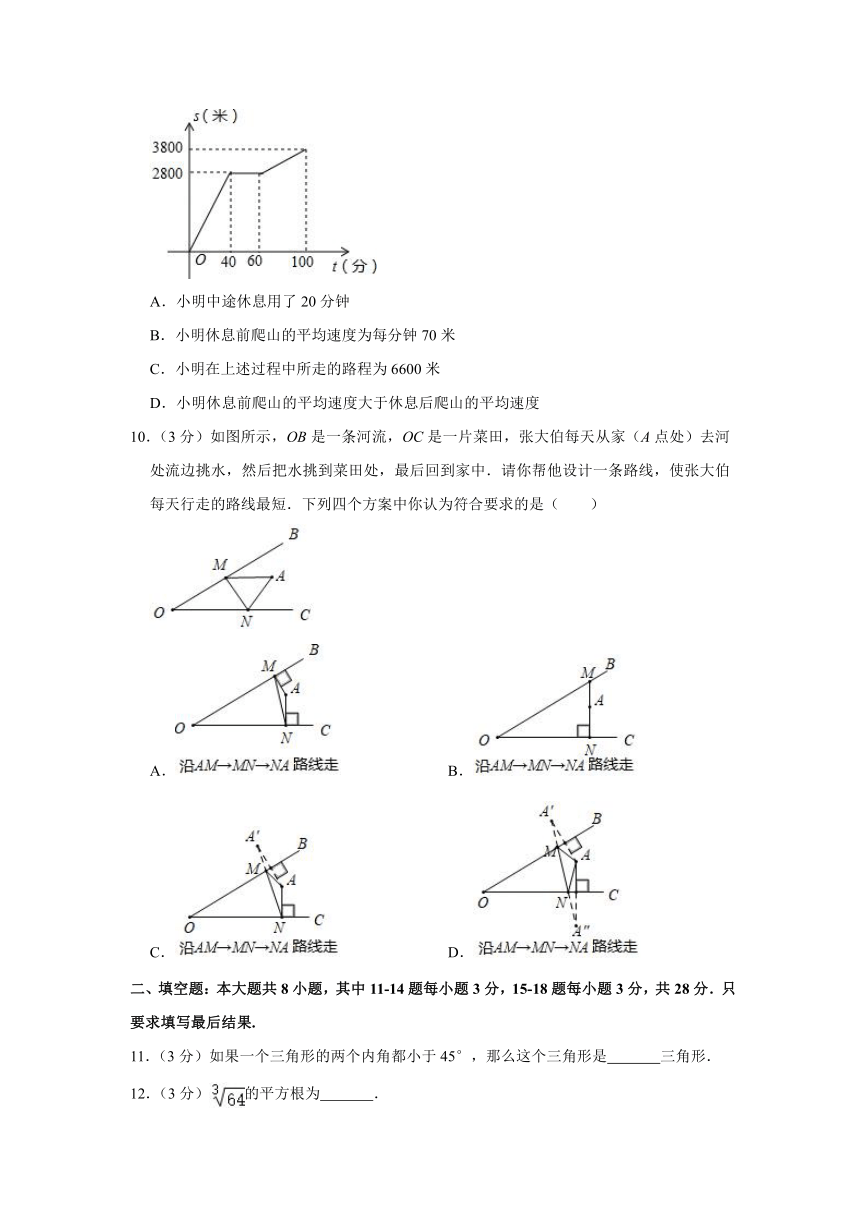
9.(3分)今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
10.(3分)如图所示,OB是一条河流,OC是一片菜田,张大伯每天从家(A点处)去河处流边挑水,然后把水挑到菜田处,最后回到家中.请你帮他设计一条路线,使张大伯每天行走的路线最短.下列四个方案中你认为符合要求的是( )
A. B.
C. D.
二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题3分,共28分.只要求填写最后结果.
11.(3分)如果一个三角形的两个内角都小于45°,那么这个三角形是 三角形.
12.(3分)的平方根为 .
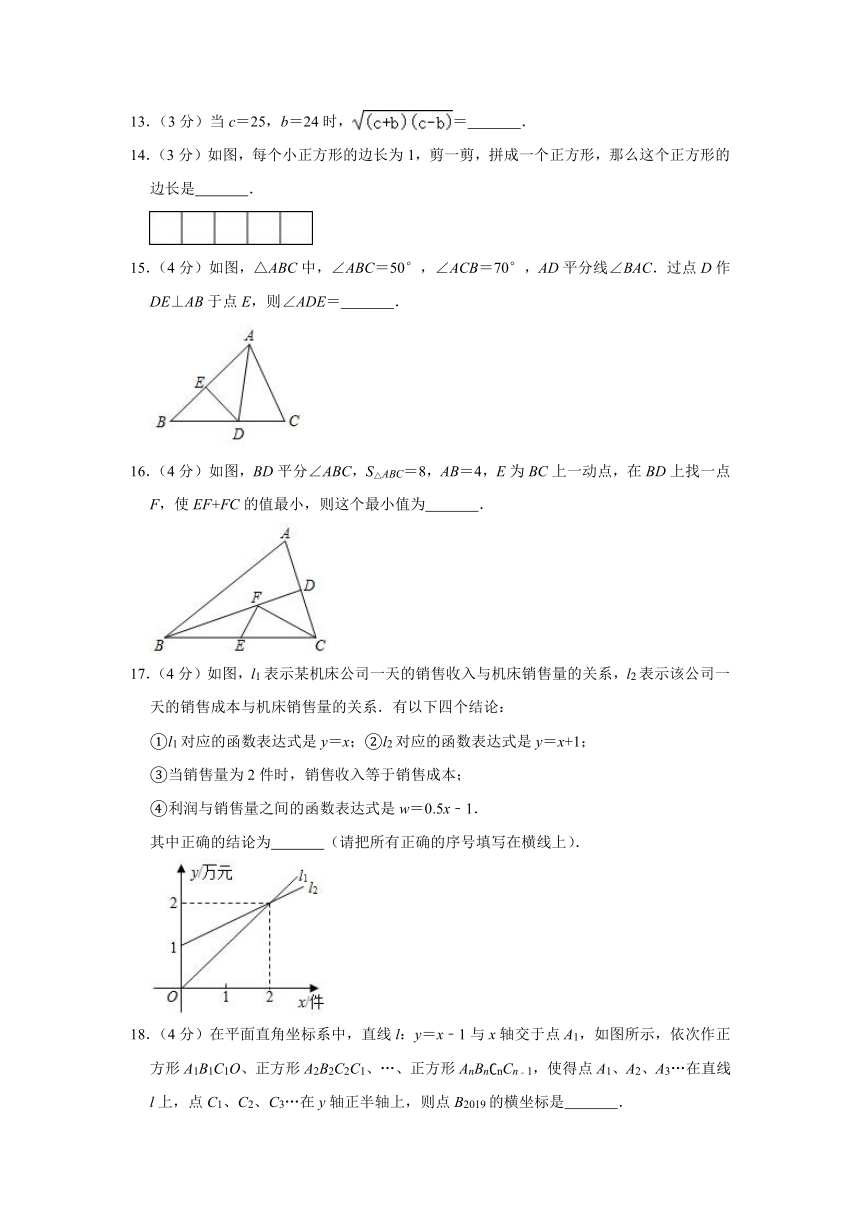
13.(3分)当c=25,b=24时,= .
14.(3分)如图,每个小正方形的边长为1,剪一剪,拼成一个正方形,那么这个正方形的边长是 .
15.(4分)如图,△ABC中,∠ABC=50°,∠ACB=70°,AD平分线∠BAC.过点D作DE⊥AB于点E,则∠ADE= .
16.(4分)如图,BD平分∠ABC,S△ABC=8,AB=4,E为BC上一动点,在BD上找一点F,使EF+FC的值最小,则这个最小值为 .
17.(4分)如图,l1表示某机床公司一天的销售收入与机床销售量的关系,l2表示该公司一天的销售成本与机床销售量的关系.有以下四个结论:
①l1对应的函数表达式是y=x;②l2对应的函数表达式是y=x+1;
③当销售量为2件时,销售收入等于销售成本;
④利润与销售量之间的函数表达式是w=0.5x﹣1.
其中正确的结论为 (请把所有正确的序号填写在横线上).
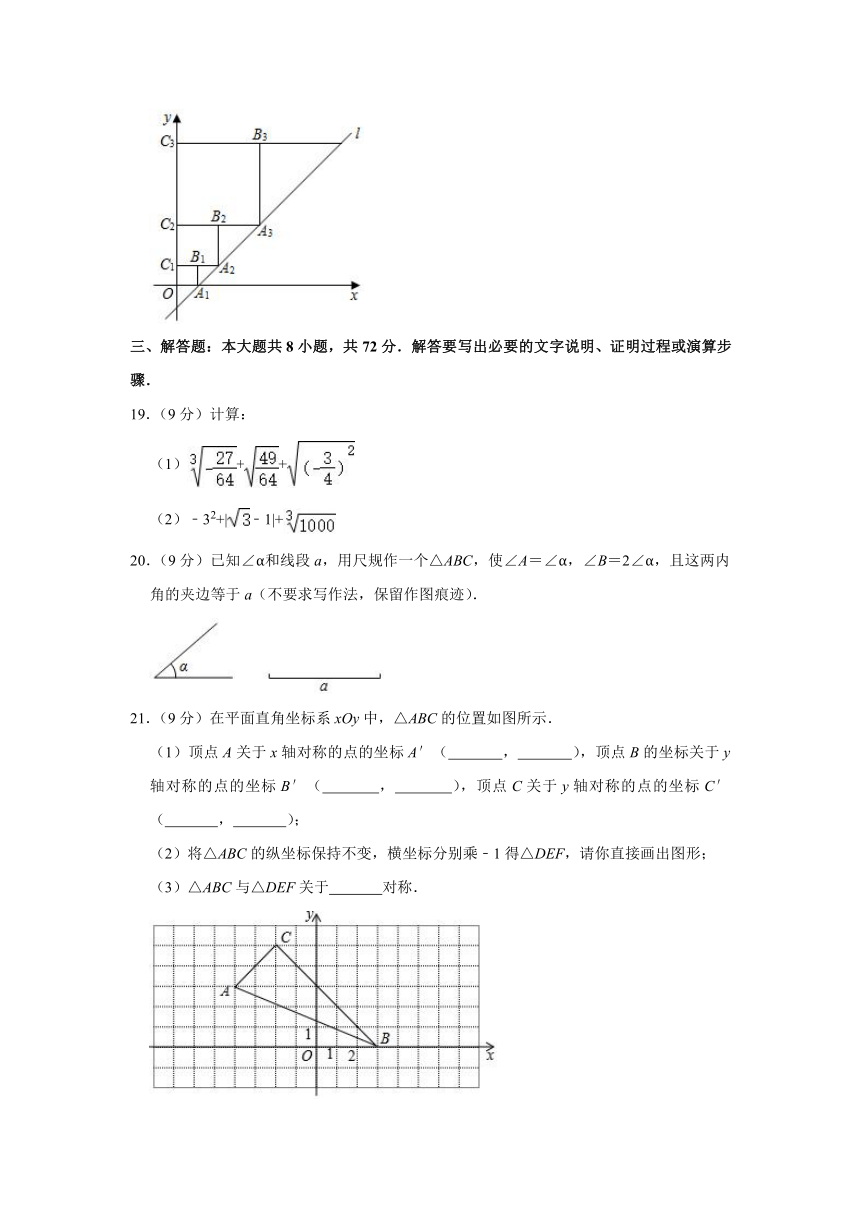
18.(4分)在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A1,如图所示,依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBn?nCn﹣1,使得点A1、A2、A3…在直线l上,点C1、C2、C3…在y轴正半轴上,则点B2019的横坐标是 .
三、解答题:本大题共8小题,共72分.解答要写出必要的文字说明、证明过程或演算步骤.
19.(9分)计算:
(1)++
(2)﹣32+|﹣1|+
20.(9分)已知∠α和线段a,用尺规作一个△ABC,使∠A=∠α,∠B=2∠α,且这两内角的夹边等于a(不要求写作法,保留作图痕迹).
21.(9分)在平面直角坐标系xOy中,△ABC的位置如图所示.
(1)顶点A关于x轴对称的点的坐标A′( , ),顶点B的坐标关于y轴对称的点的坐标B′( , ),顶点C关于y轴对称的点的坐标C′( , );
(2)将△ABC的纵坐标保持不变,横坐标分别乘﹣1得△DEF,请你直接画出图形;
(3)△ABC与△DEF关于 对称.
22.(9分)如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离:现在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度.
(1)求证:DE=AB;
(2)如果DE的长度是8m,则AB的长度是多少?
23.(9分)如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.
(1)判断∠D是否是直角,并说明理由.
(2)求四边形ABCD的面积.
24.(9分)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=x的图象交于点C(m,3).
(1)求一次函数y=kx+b的函数关系式;
(2)求△AOC的面积;
(3)若点M在第二象限,△MAB是以AB为直角边的等腰直角三角形,直接写出点M的坐标.
25.(9分)如图1,点M为直线AB上一动点,△PAB,△PMN都是等边三角形,连接BN,
(1)求证:AM=BN;
(2)写出点M在如图2所示位置时,线段AB、BM、BN三者之间的数量关系,并给出证明;
(3)点M在图3所示位置时,直接写出线段AB、BM、BN三者之间的数量关系.
26.(9分)问题情境:已知Rt△ABC的周长为30,斜边长c=13,求△ABC的面积.、
解法展示:设Rt△ABC的两直角边长分别为a,b,则a+b+c= ,因为c=13,所以a+b= ,所以(a+b)2= ,所以a2+ =289.因为a2+b2=c2,所以c2+2ab=289,所以 +2ab=289,所以ab= (第1步),所以△ABC的面积=ab=× = (第2步).
合作探究:
(1)填空.
(2)上述解题过程中,由第1步到第2步体现出来的数学思想是 (填序号).
①整体思想;②数形结合思想;③分类讨论思想.
方法迁移:
(3)已知一直角三角形的面积为24,斜边长为10,求这个直角三角形的周长.
2019-2020学年山东省东营市广饶县七年级(上)期末数学试卷(五四学制)
参考答案与试题解析
一、选择题:本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.
1.(3分)下列轴对称图形中,对称轴条数最多的是( )
A. B.
C. D.
【解答】解:A、有六条对称轴;
B、是椭圆有两条对称轴;
C、有五条对称轴;
D、有三条对称轴.
故选:A.
2.(3分)在﹣3,﹣(﹣),0,3.14,10%,0.,π,0.1010001000001…(相邻两个1之间0的个数逐次加2)中,有理数的个数为( )
A.4个 B.5个 C.6个 D.7个
【解答】解:有理数有:﹣3,﹣(﹣),0,3.14,10%,0.,共6个.
故选:C.
3.(3分)如果|3﹣a|+(b+5)2=0,那么点A(a,b)在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
【解答】解:∵|3﹣a|+(b+5)2=0,
∴3﹣a=0,b+5=0,
∴a=3,b=﹣5,
∴P(3,﹣5)在第四象限.
故选:A.
4.(3分)下列运算中:①=±;②=±7;③=﹣=﹣;④()3=9;错误的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:①=,故①错误;
②=7,故②错误;
=﹣=﹣,故③正确;
④()3=9,故④正确.
故选:B.
5.(3分)若一次函数y=kx+b的图象如图所示,则k、b的取值范围是( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
【解答】解:观察图象可得,一次函数y=kx+b的图象过一、三、四象限;
故k>0,b<0;
故选:B.
6.(3分)用尺规作图法作已知角∠AOB的平分线的步骤如下:
①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;
②分别以点D,E为圆心,以大于DE的长为半径作弧,两弧在∠AOB的内部相交于点C;
③作射线OC.
则射线OC为∠AOB的平分线.
由上述作法可得△OCD≌△OCE的依据是( )
A.SAS B.ASA C.AAS D.SSS
【解答】解:在△OEC和△ODC中,
∵,
∴△OEC≌△ODC(SSS),
故选:D.
7.(3分)如图,AB∥DE,AC∥DF,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )
A.AB=DE B.∠B=∠E C.EF=BC D.EF∥BC
【解答】解:∵AB∥DE,AC∥DF,∴∠A=∠D,
(1)AB=DE,则△ABC和△DEF中,,∴△ABC≌△DEF,故A选项错误;
(2)∠B=∠E,则△ABC和△DEF中,,∴△ABC≌△DEF,故B选项错误;
(3)EF=BC,无法证明△ABC≌△DEF(ASS);故C选项正确;
(4)∵EF∥BC,AB∥DE,∴∠B=∠E,则△ABC和△DEF中,,∴△ABC≌△DEF,故D选项错误;
故选:C.
8.(3分)在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇沿与一边垂直的方向拉向岸边,它的顶端恰好到达岸边的水面.则这根芦苇长为( )
A.12尺 B.13尺 C.6尺 D.7尺
【解答】解:设水池的深度为x尺,由题意得:
x2+52=(x+1)2,
解得:x=12,
x+1=13(尺)
答:芦苇长13尺.
故选:B.
9.(3分)今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
【解答】解:A、根据图象可知,在40~60分钟,路程没有发生变化,所以小明中途休息的时间为:60﹣40=20分钟,故正确;
B、根据图象可知,当t=40时,s=2800,所以小明休息前爬山的平均速度为:2800÷40=70(米/分钟),故B正确;
C、根据图象可知,小明在上述过程中所走的路程为3800米,故错误;
D、小明休息后的爬山的平均速度为:(3800﹣2800)÷(100﹣60)=25(米/分),小明休息前爬山的平均速度为:2800÷40=70(米/分钟),
70>25,所以小明休息前爬山的平均速度大于休息后爬山的平均速度,故正确;
故选:C.
10.(3分)如图所示,OB是一条河流,OC是一片菜田,张大伯每天从家(A点处)去河处流边挑水,然后把水挑到菜田处,最后回到家中.请你帮他设计一条路线,使张大伯每天行走的路线最短.下列四个方案中你认为符合要求的是( )
A. B.
C. D.
【解答】解:要找一条最短路线,以河流为轴,取A点的对称点A',连接A'N与河流相交于M点,再连接AM,则张大伯可沿着AM走一条直线去河边M点挑水,然后再沿MN走一条直线到菜园去,同理,画出回家的路线图如下:
故选:D.
二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题3分,共28分.只要求填写最后结果.
11.(3分)如果一个三角形的两个内角都小于45°,那么这个三角形是 钝角 三角形.
【解答】解:∵一个三角形有两个内角的度数都小于45°,
∴第三个内角的度数>180°﹣45°﹣45°,
即第三个内角的度数>90°,
∴这个三角形是三角形钝角三角形,
故答案为钝角.
12.(3分)的平方根为 ±2 .
【解答】解:∵4的立方等于64,
∴64的立方根等于4.
4的平方根是±2,
故答案为:±2.
13.(3分)当c=25,b=24时,= 7 .
【解答】解:当c=25,b=24时,
==7.
故答案为:7.
14.(3分)如图,每个小正方形的边长为1,剪一剪,拼成一个正方形,那么这个正方形的边长是 .
【解答】解:分割图形如下:
,
故这个正方形的边长是:.
故答案为:.
15.(4分)如图,△ABC中,∠ABC=50°,∠ACB=70°,AD平分线∠BAC.过点D作DE⊥AB于点E,则∠ADE= 60° .
【解答】解:∵∠ABC=50°,∠ACB=70°,
∴∠BAC=60°,
又∵AD平分线∠BAC,
∴∠BAD=30°,
又∵DE⊥AB,
∴Rt△ADE中,∠ADE=60°,
故答案为:60°.
16.(4分)如图,BD平分∠ABC,S△ABC=8,AB=4,E为BC上一动点,在BD上找一点F,使EF+FC的值最小,则这个最小值为 4 .
【解答】解:过C点作CG⊥AB,交BD与F',过F'作F'E'⊥BC,
∵BD平分∠ABC,CG⊥AB,F'E'⊥BC,
∴GF'=F'E',
∴EF+FC的值最小=GF'+F'C=CG,
∵S△ABC=8,AB=4,
∴CG===4,
∴EF+FC的最小值为4,
故答案为4.
17.(4分)如图,l1表示某机床公司一天的销售收入与机床销售量的关系,l2表示该公司一天的销售成本与机床销售量的关系.有以下四个结论:
①l1对应的函数表达式是y=x;②l2对应的函数表达式是y=x+1;
③当销售量为2件时,销售收入等于销售成本;
④利润与销售量之间的函数表达式是w=0.5x﹣1.
其中正确的结论为 ①③④ (请把所有正确的序号填写在横线上).
【解答】解:①观察图象可知直线l1经过原点,
设l1的解析式为y1=kx,
将点(2,2)代入解析式可得 2=2k,
解得k=1,
所以l1的解析式为y1=x,
故①正确;
②观察图象可知直线l2不经过原点,
设l2的解析式为y2=kx+b,
将点(0,1)、(2,2)代入解析式可得
,
解得,
所以l2的解析式为,
故②错误;
③观察图象可知,直线l1与直线l2交于点(2,2),
所以,当销售量为2时,销售收入等于销售成本,
故③正确;
④利润w=y1﹣y2==,
故④正确;
故答案为①③④
18.(4分)在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A1,如图所示,依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBn?nCn﹣1,使得点A1、A2、A3…在直线l上,点C1、C2、C3…在y轴正半轴上,则点B2019的横坐标是 22018 .
【解答】解:当y=0时,有x﹣1=0,
解得:x=1,
∴点A1的坐标为(1,0).
∵四边形A1B1C1O为正方形,
∴点B1的坐标为(1,1).
同理,可得出:A2(2,1),A3(4,3),A4(8,7),A5(16,15),…,
∴B2(2,3),B3(4,7),B4(8,15),B5(16,31),…,
∴Bn(2n﹣1,2n﹣1)(n为正整数),
∴点B2019的坐标是(22018,22019﹣1).
故答案为:22018
三、解答题:本大题共8小题,共72分.解答要写出必要的文字说明、证明过程或演算步骤.
19.(9分)计算:
(1)++
(2)﹣32+|﹣1|+
【解答】解:(1)++
=﹣++
=
(2)﹣32+|﹣1|+
=﹣9+﹣1+10
=
20.(9分)已知∠α和线段a,用尺规作一个△ABC,使∠A=∠α,∠B=2∠α,且这两内角的夹边等于a(不要求写作法,保留作图痕迹).
【解答】解:如图,△ABC为所作.
21.(9分)在平面直角坐标系xOy中,△ABC的位置如图所示.
(1)顶点A关于x轴对称的点的坐标A′( ﹣4 , ﹣3 ),顶点B的坐标关于y轴对称的点的坐标B′( ﹣3 , 0 ),顶点C关于y轴对称的点的坐标C′( 2 , 5 );
(2)将△ABC的纵坐标保持不变,横坐标分别乘﹣1得△DEF,请你直接画出图形;
(3)△ABC与△DEF关于 y轴 对称.
【解答】解:(1)顶点A关于x轴对称的点的坐标A′(﹣4,﹣3),
顶点B的坐标关于y轴对称的点的坐标B′(﹣3,0),
顶点C关于y轴对称的点的坐标C′(2,5);
故答案为:﹣4,﹣3;﹣3,0;2,5;
(2)如图所示:
(3)由(2)可知△ABC与△DEF关于y轴对称,?
故答案为:y轴.
22.(9分)如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离:现在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度.
(1)求证:DE=AB;
(2)如果DE的长度是8m,则AB的长度是多少?
【解答】(1)证明:在△CDE和△CAB中,
,
∴△CDE≌△CAB(SAS),
∴DE=AB;
(2)解:∵DE=AB,DE=8m,
∴AB=8m.
答:AB的长度是8m.
23.(9分)如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.
(1)判断∠D是否是直角,并说明理由.
(2)求四边形ABCD的面积.
【解答】解:(1)∠D是直角.
理由:连接AC,
∵∠B=90°,
∴AC2=BA2+BC2=400+225=625,
∵DA2+CD2=242+72=625,
∴AC2=DA2+DC2,
∴△ADC是直角三角形,即∠D是直角;
(2)∵S四边形ABCD=S△ABC+S△ADC,
∴S四边形ABCD=AB?BC+AD?CD
=×20×15+×24×7
=234.
24.(9分)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=x的图象交于点C(m,3).
(1)求一次函数y=kx+b的函数关系式;
(2)求△AOC的面积;
(3)若点M在第二象限,△MAB是以AB为直角边的等腰直角三角形,直接写出点M的坐标.
【解答】解:(1)∵点C(m,3)在正比例函数y=x图象上,
∴3=m,得m=2,
∴点C的坐标为(2,3)
∵点C,点B(0,2)在一次函数y=kx+b的图象上,故有,解得,
故一次函数的解析式为:y=+2;
(2)在一次函数y=x+2中,令y=0,则x+2=0,解得x=﹣4,
∴点A的坐标为(﹣4,0)
即OA=4,
∵点C的坐标为(2,3)
∴S△AOC=×4×3=6;
(3)过点M1作M1E⊥y轴于点E,过点M2作M2F⊥x轴于点F,如图,
∵点M在第二象限,△MAB是以AB为直角边的等腰直角三角形,
∴AB=BM2,
∵∠M1BE+∠ABO=90°,∠ABO+∠BAO=90°,
∴∠BAO=∠EBM1,
∵在△BEM1和△AOB中,
∴△BEM1≌△AOB(AAS),
∴BE=AO=4,M1E=BO=2,
即可得出点M的坐标为(﹣2,6);
同理可得出:△AFM2≌△AOB,
∴FA=BO=2,M2F=AO=4,
∴点M的坐标为(﹣6,4).
综上可知点M的坐标为(﹣2,6)或(﹣6,4).
25.(9分)如图1,点M为直线AB上一动点,△PAB,△PMN都是等边三角形,连接BN,
(1)求证:AM=BN;
(2)写出点M在如图2所示位置时,线段AB、BM、BN三者之间的数量关系,并给出证明;
(3)点M在图3所示位置时,直接写出线段AB、BM、BN三者之间的数量关系.
【解答】(1)证明:如图1,∵△PAB和△PMN是等边三角形,
∴∠BPA=∠MPN=60°,AB=BP=AP,PM=PN=MN,
∴∠BPA﹣∠MPB=∠MPN﹣∠MPB,即∠APM=∠BPN.
?在△APM和△PBN中,
,
∴△APM≌△BPN(SAS),
∴AM=BN;
(2)解:BN=AB+BM;
理由如下:如图2,?∵△PAB和△PMN是等边三角形,
∴∠APB=∠MPN=60°,AB=BP=AP,PM=PN=MN,
∴∠BPA+∠MPB=∠MPN+∠MPB,即∠APM=∠BPN,
?在△APM和△PBN中,
,
∴△APM≌△BPN(SAS),
∴AM=BN,
∴BN=AM=AB+BM,即BN=AB+BM;
(3)解:BN=BM﹣AB,
理由如下:如图3,由(2)可知,△APM≌△BPN,
∴AM=BN,
∴BN=AM=BM﹣AB.
26.(9分)问题情境:已知Rt△ABC的周长为30,斜边长c=13,求△ABC的面积.、
解法展示:设Rt△ABC的两直角边长分别为a,b,则a+b+c= 30 ,因为c=13,所以a+b= 17 ,所以(a+b)2= 289 ,所以a2+ b2+2ab =289.因为a2+b2=c2,所以c2+2ab=289,所以 169 +2ab=289,所以ab= 60 (第1步),所以△ABC的面积=ab=× 60 = 30 (第2步).
合作探究:
(1)填空.
(2)上述解题过程中,由第1步到第2步体现出来的数学思想是 ① (填序号).
①整体思想;②数形结合思想;③分类讨论思想.
方法迁移:
(3)已知一直角三角形的面积为24,斜边长为10,求这个直角三角形的周长.
【解答】解:(1)解法展示:设Rt△ABC的两直角边长分别为a,b,则a+b+c=30,因为c=13,所以a+b=17,所以(a+b)2=289,所以a2+b2+2ab=289.因为a2+b2=c2,所以c2+2ab=289,所以169+2ab=289,所以ab=60(第1步),所以△ABC的面积=ab=×60=30(第2步).
合作探究:
(2)上述解题过程中,由第1步到第2步体现出来的数学思想是①.
方法迁移:
(3)设直角三角形的两直角边分别是a、b(a<b,且a、b均为正数),则
,
解得.
所以这个直角三角形的周长是:6+8+10=24.
故答案为:30,17,289,b2+2ab,169,60,60,30;①.
一、选择题:本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.
1.(3分)下列轴对称图形中,对称轴条数最多的是( )
A. B.
C. D.
2.(3分)在﹣3,﹣(﹣),0,3.14,10%,0.,π,0.1010001000001…(相邻两个1之间0的个数逐次加2)中,有理数的个数为( )
A.4个 B.5个 C.6个 D.7个
3.(3分)如果|3﹣a|+(b+5)2=0,那么点A(a,b)在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
4.(3分)下列运算中:①=±;②=±7;③=﹣=﹣;④()3=9;错误的有( )
A.1个 B.2个 C.3个 D.4个
5.(3分)若一次函数y=kx+b的图象如图所示,则k、b的取值范围是( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
6.(3分)用尺规作图法作已知角∠AOB的平分线的步骤如下:
①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;
②分别以点D,E为圆心,以大于DE的长为半径作弧,两弧在∠AOB的内部相交于点C;
③作射线OC.
则射线OC为∠AOB的平分线.
由上述作法可得△OCD≌△OCE的依据是( )
A.SAS B.ASA C.AAS D.SSS
7.(3分)如图,AB∥DE,AC∥DF,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )
A.AB=DE B.∠B=∠E C.EF=BC D.EF∥BC
8.(3分)在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇沿与一边垂直的方向拉向岸边,它的顶端恰好到达岸边的水面.则这根芦苇长为( )
A.12尺 B.13尺 C.6尺 D.7尺
9.(3分)今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
10.(3分)如图所示,OB是一条河流,OC是一片菜田,张大伯每天从家(A点处)去河处流边挑水,然后把水挑到菜田处,最后回到家中.请你帮他设计一条路线,使张大伯每天行走的路线最短.下列四个方案中你认为符合要求的是( )
A. B.
C. D.
二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题3分,共28分.只要求填写最后结果.
11.(3分)如果一个三角形的两个内角都小于45°,那么这个三角形是 三角形.
12.(3分)的平方根为 .
13.(3分)当c=25,b=24时,= .
14.(3分)如图,每个小正方形的边长为1,剪一剪,拼成一个正方形,那么这个正方形的边长是 .
15.(4分)如图,△ABC中,∠ABC=50°,∠ACB=70°,AD平分线∠BAC.过点D作DE⊥AB于点E,则∠ADE= .
16.(4分)如图,BD平分∠ABC,S△ABC=8,AB=4,E为BC上一动点,在BD上找一点F,使EF+FC的值最小,则这个最小值为 .
17.(4分)如图,l1表示某机床公司一天的销售收入与机床销售量的关系,l2表示该公司一天的销售成本与机床销售量的关系.有以下四个结论:
①l1对应的函数表达式是y=x;②l2对应的函数表达式是y=x+1;
③当销售量为2件时,销售收入等于销售成本;
④利润与销售量之间的函数表达式是w=0.5x﹣1.
其中正确的结论为 (请把所有正确的序号填写在横线上).
18.(4分)在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A1,如图所示,依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBn?nCn﹣1,使得点A1、A2、A3…在直线l上,点C1、C2、C3…在y轴正半轴上,则点B2019的横坐标是 .
三、解答题:本大题共8小题,共72分.解答要写出必要的文字说明、证明过程或演算步骤.
19.(9分)计算:
(1)++
(2)﹣32+|﹣1|+
20.(9分)已知∠α和线段a,用尺规作一个△ABC,使∠A=∠α,∠B=2∠α,且这两内角的夹边等于a(不要求写作法,保留作图痕迹).
21.(9分)在平面直角坐标系xOy中,△ABC的位置如图所示.
(1)顶点A关于x轴对称的点的坐标A′( , ),顶点B的坐标关于y轴对称的点的坐标B′( , ),顶点C关于y轴对称的点的坐标C′( , );
(2)将△ABC的纵坐标保持不变,横坐标分别乘﹣1得△DEF,请你直接画出图形;
(3)△ABC与△DEF关于 对称.
22.(9分)如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离:现在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度.
(1)求证:DE=AB;
(2)如果DE的长度是8m,则AB的长度是多少?
23.(9分)如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.
(1)判断∠D是否是直角,并说明理由.
(2)求四边形ABCD的面积.
24.(9分)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=x的图象交于点C(m,3).
(1)求一次函数y=kx+b的函数关系式;
(2)求△AOC的面积;
(3)若点M在第二象限,△MAB是以AB为直角边的等腰直角三角形,直接写出点M的坐标.
25.(9分)如图1,点M为直线AB上一动点,△PAB,△PMN都是等边三角形,连接BN,
(1)求证:AM=BN;
(2)写出点M在如图2所示位置时,线段AB、BM、BN三者之间的数量关系,并给出证明;
(3)点M在图3所示位置时,直接写出线段AB、BM、BN三者之间的数量关系.
26.(9分)问题情境:已知Rt△ABC的周长为30,斜边长c=13,求△ABC的面积.、
解法展示:设Rt△ABC的两直角边长分别为a,b,则a+b+c= ,因为c=13,所以a+b= ,所以(a+b)2= ,所以a2+ =289.因为a2+b2=c2,所以c2+2ab=289,所以 +2ab=289,所以ab= (第1步),所以△ABC的面积=ab=× = (第2步).
合作探究:
(1)填空.
(2)上述解题过程中,由第1步到第2步体现出来的数学思想是 (填序号).
①整体思想;②数形结合思想;③分类讨论思想.
方法迁移:
(3)已知一直角三角形的面积为24,斜边长为10,求这个直角三角形的周长.
2019-2020学年山东省东营市广饶县七年级(上)期末数学试卷(五四学制)
参考答案与试题解析
一、选择题:本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.
1.(3分)下列轴对称图形中,对称轴条数最多的是( )
A. B.
C. D.
【解答】解:A、有六条对称轴;
B、是椭圆有两条对称轴;
C、有五条对称轴;
D、有三条对称轴.
故选:A.
2.(3分)在﹣3,﹣(﹣),0,3.14,10%,0.,π,0.1010001000001…(相邻两个1之间0的个数逐次加2)中,有理数的个数为( )
A.4个 B.5个 C.6个 D.7个
【解答】解:有理数有:﹣3,﹣(﹣),0,3.14,10%,0.,共6个.
故选:C.
3.(3分)如果|3﹣a|+(b+5)2=0,那么点A(a,b)在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
【解答】解:∵|3﹣a|+(b+5)2=0,
∴3﹣a=0,b+5=0,
∴a=3,b=﹣5,
∴P(3,﹣5)在第四象限.
故选:A.
4.(3分)下列运算中:①=±;②=±7;③=﹣=﹣;④()3=9;错误的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:①=,故①错误;
②=7,故②错误;
=﹣=﹣,故③正确;
④()3=9,故④正确.
故选:B.
5.(3分)若一次函数y=kx+b的图象如图所示,则k、b的取值范围是( )
A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0
【解答】解:观察图象可得,一次函数y=kx+b的图象过一、三、四象限;
故k>0,b<0;
故选:B.
6.(3分)用尺规作图法作已知角∠AOB的平分线的步骤如下:
①以点O为圆心,任意长为半径作弧,交OB于点D,交OA于点E;
②分别以点D,E为圆心,以大于DE的长为半径作弧,两弧在∠AOB的内部相交于点C;
③作射线OC.
则射线OC为∠AOB的平分线.
由上述作法可得△OCD≌△OCE的依据是( )
A.SAS B.ASA C.AAS D.SSS
【解答】解:在△OEC和△ODC中,
∵,
∴△OEC≌△ODC(SSS),
故选:D.
7.(3分)如图,AB∥DE,AC∥DF,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )
A.AB=DE B.∠B=∠E C.EF=BC D.EF∥BC
【解答】解:∵AB∥DE,AC∥DF,∴∠A=∠D,
(1)AB=DE,则△ABC和△DEF中,,∴△ABC≌△DEF,故A选项错误;
(2)∠B=∠E,则△ABC和△DEF中,,∴△ABC≌△DEF,故B选项错误;
(3)EF=BC,无法证明△ABC≌△DEF(ASS);故C选项正确;
(4)∵EF∥BC,AB∥DE,∴∠B=∠E,则△ABC和△DEF中,,∴△ABC≌△DEF,故D选项错误;
故选:C.
8.(3分)在我国古代数学著作《九章算术》中记载了一个有趣的问题,这个问题的意思是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇沿与一边垂直的方向拉向岸边,它的顶端恰好到达岸边的水面.则这根芦苇长为( )
A.12尺 B.13尺 C.6尺 D.7尺
【解答】解:设水池的深度为x尺,由题意得:
x2+52=(x+1)2,
解得:x=12,
x+1=13(尺)
答:芦苇长13尺.
故选:B.
9.(3分)今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
【解答】解:A、根据图象可知,在40~60分钟,路程没有发生变化,所以小明中途休息的时间为:60﹣40=20分钟,故正确;
B、根据图象可知,当t=40时,s=2800,所以小明休息前爬山的平均速度为:2800÷40=70(米/分钟),故B正确;
C、根据图象可知,小明在上述过程中所走的路程为3800米,故错误;
D、小明休息后的爬山的平均速度为:(3800﹣2800)÷(100﹣60)=25(米/分),小明休息前爬山的平均速度为:2800÷40=70(米/分钟),
70>25,所以小明休息前爬山的平均速度大于休息后爬山的平均速度,故正确;
故选:C.
10.(3分)如图所示,OB是一条河流,OC是一片菜田,张大伯每天从家(A点处)去河处流边挑水,然后把水挑到菜田处,最后回到家中.请你帮他设计一条路线,使张大伯每天行走的路线最短.下列四个方案中你认为符合要求的是( )
A. B.
C. D.
【解答】解:要找一条最短路线,以河流为轴,取A点的对称点A',连接A'N与河流相交于M点,再连接AM,则张大伯可沿着AM走一条直线去河边M点挑水,然后再沿MN走一条直线到菜园去,同理,画出回家的路线图如下:
故选:D.
二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题3分,共28分.只要求填写最后结果.
11.(3分)如果一个三角形的两个内角都小于45°,那么这个三角形是 钝角 三角形.
【解答】解:∵一个三角形有两个内角的度数都小于45°,
∴第三个内角的度数>180°﹣45°﹣45°,
即第三个内角的度数>90°,
∴这个三角形是三角形钝角三角形,
故答案为钝角.
12.(3分)的平方根为 ±2 .
【解答】解:∵4的立方等于64,
∴64的立方根等于4.
4的平方根是±2,
故答案为:±2.
13.(3分)当c=25,b=24时,= 7 .
【解答】解:当c=25,b=24时,
==7.
故答案为:7.
14.(3分)如图,每个小正方形的边长为1,剪一剪,拼成一个正方形,那么这个正方形的边长是 .
【解答】解:分割图形如下:
,
故这个正方形的边长是:.
故答案为:.
15.(4分)如图,△ABC中,∠ABC=50°,∠ACB=70°,AD平分线∠BAC.过点D作DE⊥AB于点E,则∠ADE= 60° .
【解答】解:∵∠ABC=50°,∠ACB=70°,
∴∠BAC=60°,
又∵AD平分线∠BAC,
∴∠BAD=30°,
又∵DE⊥AB,
∴Rt△ADE中,∠ADE=60°,
故答案为:60°.
16.(4分)如图,BD平分∠ABC,S△ABC=8,AB=4,E为BC上一动点,在BD上找一点F,使EF+FC的值最小,则这个最小值为 4 .
【解答】解:过C点作CG⊥AB,交BD与F',过F'作F'E'⊥BC,
∵BD平分∠ABC,CG⊥AB,F'E'⊥BC,
∴GF'=F'E',
∴EF+FC的值最小=GF'+F'C=CG,
∵S△ABC=8,AB=4,
∴CG===4,
∴EF+FC的最小值为4,
故答案为4.
17.(4分)如图,l1表示某机床公司一天的销售收入与机床销售量的关系,l2表示该公司一天的销售成本与机床销售量的关系.有以下四个结论:
①l1对应的函数表达式是y=x;②l2对应的函数表达式是y=x+1;
③当销售量为2件时,销售收入等于销售成本;
④利润与销售量之间的函数表达式是w=0.5x﹣1.
其中正确的结论为 ①③④ (请把所有正确的序号填写在横线上).
【解答】解:①观察图象可知直线l1经过原点,
设l1的解析式为y1=kx,
将点(2,2)代入解析式可得 2=2k,
解得k=1,
所以l1的解析式为y1=x,
故①正确;
②观察图象可知直线l2不经过原点,
设l2的解析式为y2=kx+b,
将点(0,1)、(2,2)代入解析式可得
,
解得,
所以l2的解析式为,
故②错误;
③观察图象可知,直线l1与直线l2交于点(2,2),
所以,当销售量为2时,销售收入等于销售成本,
故③正确;
④利润w=y1﹣y2==,
故④正确;
故答案为①③④
18.(4分)在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A1,如图所示,依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBn?nCn﹣1,使得点A1、A2、A3…在直线l上,点C1、C2、C3…在y轴正半轴上,则点B2019的横坐标是 22018 .
【解答】解:当y=0时,有x﹣1=0,
解得:x=1,
∴点A1的坐标为(1,0).
∵四边形A1B1C1O为正方形,
∴点B1的坐标为(1,1).
同理,可得出:A2(2,1),A3(4,3),A4(8,7),A5(16,15),…,
∴B2(2,3),B3(4,7),B4(8,15),B5(16,31),…,
∴Bn(2n﹣1,2n﹣1)(n为正整数),
∴点B2019的坐标是(22018,22019﹣1).
故答案为:22018
三、解答题:本大题共8小题,共72分.解答要写出必要的文字说明、证明过程或演算步骤.
19.(9分)计算:
(1)++
(2)﹣32+|﹣1|+
【解答】解:(1)++
=﹣++
=
(2)﹣32+|﹣1|+
=﹣9+﹣1+10
=
20.(9分)已知∠α和线段a,用尺规作一个△ABC,使∠A=∠α,∠B=2∠α,且这两内角的夹边等于a(不要求写作法,保留作图痕迹).
【解答】解:如图,△ABC为所作.
21.(9分)在平面直角坐标系xOy中,△ABC的位置如图所示.
(1)顶点A关于x轴对称的点的坐标A′( ﹣4 , ﹣3 ),顶点B的坐标关于y轴对称的点的坐标B′( ﹣3 , 0 ),顶点C关于y轴对称的点的坐标C′( 2 , 5 );
(2)将△ABC的纵坐标保持不变,横坐标分别乘﹣1得△DEF,请你直接画出图形;
(3)△ABC与△DEF关于 y轴 对称.
【解答】解:(1)顶点A关于x轴对称的点的坐标A′(﹣4,﹣3),
顶点B的坐标关于y轴对称的点的坐标B′(﹣3,0),
顶点C关于y轴对称的点的坐标C′(2,5);
故答案为:﹣4,﹣3;﹣3,0;2,5;
(2)如图所示:
(3)由(2)可知△ABC与△DEF关于y轴对称,?
故答案为:y轴.
22.(9分)如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离:现在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度.
(1)求证:DE=AB;
(2)如果DE的长度是8m,则AB的长度是多少?
【解答】(1)证明:在△CDE和△CAB中,
,
∴△CDE≌△CAB(SAS),
∴DE=AB;
(2)解:∵DE=AB,DE=8m,
∴AB=8m.
答:AB的长度是8m.
23.(9分)如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.
(1)判断∠D是否是直角,并说明理由.
(2)求四边形ABCD的面积.
【解答】解:(1)∠D是直角.
理由:连接AC,
∵∠B=90°,
∴AC2=BA2+BC2=400+225=625,
∵DA2+CD2=242+72=625,
∴AC2=DA2+DC2,
∴△ADC是直角三角形,即∠D是直角;
(2)∵S四边形ABCD=S△ABC+S△ADC,
∴S四边形ABCD=AB?BC+AD?CD
=×20×15+×24×7
=234.
24.(9分)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=x的图象交于点C(m,3).
(1)求一次函数y=kx+b的函数关系式;
(2)求△AOC的面积;
(3)若点M在第二象限,△MAB是以AB为直角边的等腰直角三角形,直接写出点M的坐标.
【解答】解:(1)∵点C(m,3)在正比例函数y=x图象上,
∴3=m,得m=2,
∴点C的坐标为(2,3)
∵点C,点B(0,2)在一次函数y=kx+b的图象上,故有,解得,
故一次函数的解析式为:y=+2;
(2)在一次函数y=x+2中,令y=0,则x+2=0,解得x=﹣4,
∴点A的坐标为(﹣4,0)
即OA=4,
∵点C的坐标为(2,3)
∴S△AOC=×4×3=6;
(3)过点M1作M1E⊥y轴于点E,过点M2作M2F⊥x轴于点F,如图,
∵点M在第二象限,△MAB是以AB为直角边的等腰直角三角形,
∴AB=BM2,
∵∠M1BE+∠ABO=90°,∠ABO+∠BAO=90°,
∴∠BAO=∠EBM1,
∵在△BEM1和△AOB中,
∴△BEM1≌△AOB(AAS),
∴BE=AO=4,M1E=BO=2,
即可得出点M的坐标为(﹣2,6);
同理可得出:△AFM2≌△AOB,
∴FA=BO=2,M2F=AO=4,
∴点M的坐标为(﹣6,4).
综上可知点M的坐标为(﹣2,6)或(﹣6,4).
25.(9分)如图1,点M为直线AB上一动点,△PAB,△PMN都是等边三角形,连接BN,
(1)求证:AM=BN;
(2)写出点M在如图2所示位置时,线段AB、BM、BN三者之间的数量关系,并给出证明;
(3)点M在图3所示位置时,直接写出线段AB、BM、BN三者之间的数量关系.
【解答】(1)证明:如图1,∵△PAB和△PMN是等边三角形,
∴∠BPA=∠MPN=60°,AB=BP=AP,PM=PN=MN,
∴∠BPA﹣∠MPB=∠MPN﹣∠MPB,即∠APM=∠BPN.
?在△APM和△PBN中,
,
∴△APM≌△BPN(SAS),
∴AM=BN;
(2)解:BN=AB+BM;
理由如下:如图2,?∵△PAB和△PMN是等边三角形,
∴∠APB=∠MPN=60°,AB=BP=AP,PM=PN=MN,
∴∠BPA+∠MPB=∠MPN+∠MPB,即∠APM=∠BPN,
?在△APM和△PBN中,
,
∴△APM≌△BPN(SAS),
∴AM=BN,
∴BN=AM=AB+BM,即BN=AB+BM;
(3)解:BN=BM﹣AB,
理由如下:如图3,由(2)可知,△APM≌△BPN,
∴AM=BN,
∴BN=AM=BM﹣AB.
26.(9分)问题情境:已知Rt△ABC的周长为30,斜边长c=13,求△ABC的面积.、
解法展示:设Rt△ABC的两直角边长分别为a,b,则a+b+c= 30 ,因为c=13,所以a+b= 17 ,所以(a+b)2= 289 ,所以a2+ b2+2ab =289.因为a2+b2=c2,所以c2+2ab=289,所以 169 +2ab=289,所以ab= 60 (第1步),所以△ABC的面积=ab=× 60 = 30 (第2步).
合作探究:
(1)填空.
(2)上述解题过程中,由第1步到第2步体现出来的数学思想是 ① (填序号).
①整体思想;②数形结合思想;③分类讨论思想.
方法迁移:
(3)已知一直角三角形的面积为24,斜边长为10,求这个直角三角形的周长.
【解答】解:(1)解法展示:设Rt△ABC的两直角边长分别为a,b,则a+b+c=30,因为c=13,所以a+b=17,所以(a+b)2=289,所以a2+b2+2ab=289.因为a2+b2=c2,所以c2+2ab=289,所以169+2ab=289,所以ab=60(第1步),所以△ABC的面积=ab=×60=30(第2步).
合作探究:
(2)上述解题过程中,由第1步到第2步体现出来的数学思想是①.
方法迁移:
(3)设直角三角形的两直角边分别是a、b(a<b,且a、b均为正数),则
,
解得.
所以这个直角三角形的周长是:6+8+10=24.
故答案为:30,17,289,b2+2ab,169,60,60,30;①.
同课章节目录
