人教版八年级下册数学19.2一次函数专题复习教案
文档属性
| 名称 | 人教版八年级下册数学19.2一次函数专题复习教案 |  | |
| 格式 | zip | ||
| 文件大小 | 341.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-28 12:11:35 | ||
图片预览


文档简介
课题: 一次函数的图像、性质及解析式的确定
教学目标: 1、会画函数的图像,掌握一次函数及正比例函数图像的区别与联系; 2、掌握一次函数及正比例函数的性质及特点; 3、了解函数表达式的几种形式,及掌握一次函数表达式的确定方法。
教学内容:1、一次函数及正比例函数的概念及图像; 2、一次函数及正比例函数的性质及特点; 3、函数表达式的几种形式及一次函数表达式的确定方法。
重点难点:重点:一次函数及正比例函数的图像及性质,以及利用待定系数法求一次函数的解析式。 难点:待定系数法求一次函数的解析式;一次函数与正比例函数的关系。
教学策略: 讲练结合
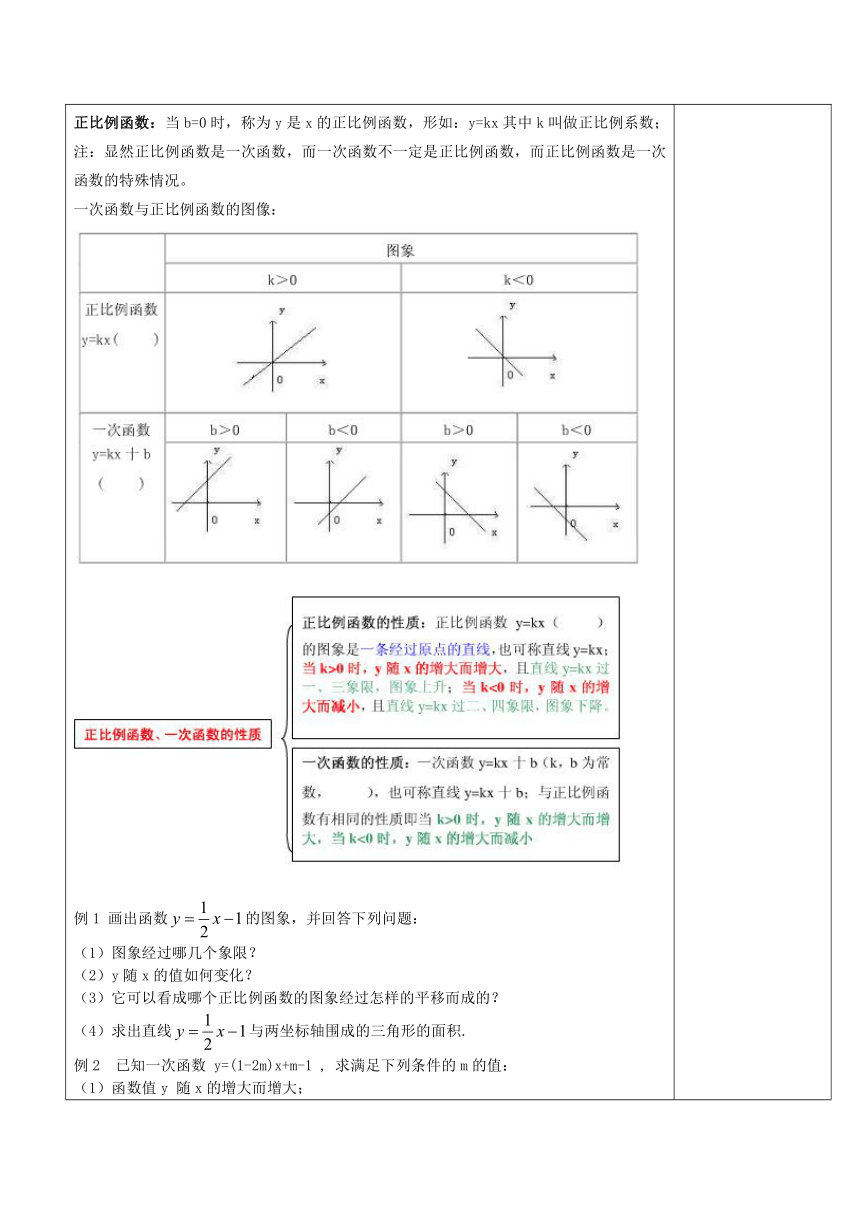
教学过程设计:一、一次函数的图像1、函数的几种表达方式: 2、函数的概念:对于一个函数,如果把自变量与函数的每对对应值分别作为点的横纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图像。 注:函数解析式是一个二元方程,这个方程的解分别是这个函数图像上点的横坐标、纵坐标;函数图像的画法:列表、描点、连线。 3、一次函数与正比例函数的概念、图像与性质一次函数:形如y=kx+b(k≠0)函数叫做x的一次函数正比例函数:当b=0时,称为y是x的正比例函数,形如:y=kx其中k叫做正比例系数; 注:显然正比例函数是一次函数,而一次函数不一定是正比例函数,而正比例函数是一次函数的特殊情况。 一次函数与正比例函数的图像: 例1 画出函数的图象,并回答下列问题: (1)图象经过哪几个象限? (2)y随x的值如何变化? (3)它可以看成哪个正比例函数的图象经过怎样的平移而成的? (4)求出直线与两坐标轴围成的三角形的面积. 例2 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值: (1)函数值y 随x的增大而增大; (2)函数图象与y 轴的负半轴相交; (3)函数的图象过第二、三、四象限; (4)函数的图象过原点。例3 甲、乙二人沿相同的路线由A到B匀速行进,A,B两地间的路程为20km.他们行进的路程s(km)与甲出发后的时间t(h)之间的函数图像下图所示.根据图像信息,下列说法正确的是(????) A.甲的速度是4?km/ h??? B.乙的速度是10 km/ h C.乙比甲晚出发1 h????? D.甲比乙晚到B地3 h 例4 一次函数y=6x+1的图象不经过( ) A?第一象限 B第二象限 C第三象限 ?D第四象限例5 如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( ).例6 如下图,直线的解析表达式为,且与轴交于点,直线经过点,直线,交于点. (1)求点的坐标;(2)求直线的解析表达式;(3)求的面积; (4)在直线上存在异于点的另一点,使得与的面积相等,请直接写出点的坐标.二、一次函数表达式的确定例1 已知一次函数的图像过点(2,-1),求这个函数的解析式。例2 已知某个一次函数的图像与x轴、y轴的交点坐标分别是(-2,0)、(0,4),则这个函数的解析式为_____________。 例3 已知某个一次函数的图像如图所示,则该函数的解析式为__________。? y
2
O 1 x
?例4 在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图10所示,请根据图象所提供的信息解答下列问题: (1)甲、乙两根蜡烛燃烧前的高度分别是????????????????,从点燃到燃尽所用的时间分别是?????????????。 (2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式; (3)燃烧多长时间时,甲、乙两根蜡烛的高度相等(不考虑都燃尽时的情况)?在什么事件段内,甲蜡烛比乙蜡烛高?在什么时间段内,甲蜡烛比乙蜡烛低?三、一次函数解析式的其他题型1. 定义型 例1. 已知函数是一次函数,求其解析式。2、斜截型 例2. 已知直线与直线平行,且在y轴上的截距为2,则直线的解析式为___________。3、平移型 例3. 把直线向下平移2个单位得到的图像解析式为___________。4、面积型 例4. 已知直线与两坐标轴所围成的三角形面积等于4,则直线解析式为__________。 5、对称型 若直线与直线关于 (1)x轴对称,则直线l的解析式为 (2)y轴对称,则直线l的解析式为 例5. 若直线l与直线关于y轴对称,则直线l的解析式为____________。四、课后练习一、选择题 1、若正比例函数的图像经过点(-1,2),则这个图像必经过点( )A.(1,2) B.(-1,-2) C.(2,-1) D.(1,-2)2、P1(x1,y1),P2(x2,y2)是正比例函数y= -x图象上的两点,则下列判断正确的是( ) A.y1>y2 B.y1y2 D.当x1
x/小时
y/千米
x/小时
y/千米
600
14
6
O
F
E
C
D
PAGE
教学目标: 1、会画函数的图像,掌握一次函数及正比例函数图像的区别与联系; 2、掌握一次函数及正比例函数的性质及特点; 3、了解函数表达式的几种形式,及掌握一次函数表达式的确定方法。
教学内容:1、一次函数及正比例函数的概念及图像; 2、一次函数及正比例函数的性质及特点; 3、函数表达式的几种形式及一次函数表达式的确定方法。
重点难点:重点:一次函数及正比例函数的图像及性质,以及利用待定系数法求一次函数的解析式。 难点:待定系数法求一次函数的解析式;一次函数与正比例函数的关系。
教学策略: 讲练结合
教学过程设计:一、一次函数的图像1、函数的几种表达方式: 2、函数的概念:对于一个函数,如果把自变量与函数的每对对应值分别作为点的横纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图像。 注:函数解析式是一个二元方程,这个方程的解分别是这个函数图像上点的横坐标、纵坐标;函数图像的画法:列表、描点、连线。 3、一次函数与正比例函数的概念、图像与性质一次函数:形如y=kx+b(k≠0)函数叫做x的一次函数正比例函数:当b=0时,称为y是x的正比例函数,形如:y=kx其中k叫做正比例系数; 注:显然正比例函数是一次函数,而一次函数不一定是正比例函数,而正比例函数是一次函数的特殊情况。 一次函数与正比例函数的图像: 例1 画出函数的图象,并回答下列问题: (1)图象经过哪几个象限? (2)y随x的值如何变化? (3)它可以看成哪个正比例函数的图象经过怎样的平移而成的? (4)求出直线与两坐标轴围成的三角形的面积. 例2 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值: (1)函数值y 随x的增大而增大; (2)函数图象与y 轴的负半轴相交; (3)函数的图象过第二、三、四象限; (4)函数的图象过原点。例3 甲、乙二人沿相同的路线由A到B匀速行进,A,B两地间的路程为20km.他们行进的路程s(km)与甲出发后的时间t(h)之间的函数图像下图所示.根据图像信息,下列说法正确的是(????) A.甲的速度是4?km/ h??? B.乙的速度是10 km/ h C.乙比甲晚出发1 h????? D.甲比乙晚到B地3 h 例4 一次函数y=6x+1的图象不经过( ) A?第一象限 B第二象限 C第三象限 ?D第四象限例5 如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( ).例6 如下图,直线的解析表达式为,且与轴交于点,直线经过点,直线,交于点. (1)求点的坐标;(2)求直线的解析表达式;(3)求的面积; (4)在直线上存在异于点的另一点,使得与的面积相等,请直接写出点的坐标.二、一次函数表达式的确定例1 已知一次函数的图像过点(2,-1),求这个函数的解析式。例2 已知某个一次函数的图像与x轴、y轴的交点坐标分别是(-2,0)、(0,4),则这个函数的解析式为_____________。 例3 已知某个一次函数的图像如图所示,则该函数的解析式为__________。? y
2
O 1 x
?例4 在一次蜡烛燃烧试验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(厘米)与燃烧时间x(小时)之间的关系如图10所示,请根据图象所提供的信息解答下列问题: (1)甲、乙两根蜡烛燃烧前的高度分别是????????????????,从点燃到燃尽所用的时间分别是?????????????。 (2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式; (3)燃烧多长时间时,甲、乙两根蜡烛的高度相等(不考虑都燃尽时的情况)?在什么事件段内,甲蜡烛比乙蜡烛高?在什么时间段内,甲蜡烛比乙蜡烛低?三、一次函数解析式的其他题型1. 定义型 例1. 已知函数是一次函数,求其解析式。2、斜截型 例2. 已知直线与直线平行,且在y轴上的截距为2,则直线的解析式为___________。3、平移型 例3. 把直线向下平移2个单位得到的图像解析式为___________。4、面积型 例4. 已知直线与两坐标轴所围成的三角形面积等于4,则直线解析式为__________。 5、对称型 若直线与直线关于 (1)x轴对称,则直线l的解析式为 (2)y轴对称,则直线l的解析式为 例5. 若直线l与直线关于y轴对称,则直线l的解析式为____________。四、课后练习一、选择题 1、若正比例函数的图像经过点(-1,2),则这个图像必经过点( )A.(1,2) B.(-1,-2) C.(2,-1) D.(1,-2)2、P1(x1,y1),P2(x2,y2)是正比例函数y= -x图象上的两点,则下列判断正确的是( ) A.y1>y2 B.y1
x/小时
y/千米
x/小时
y/千米
600
14
6
O
F
E
C
D
PAGE
