16.3 可化为一元一次方程的分式方程课件(共23张PPT)
文档属性
| 名称 | 16.3 可化为一元一次方程的分式方程课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 18.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-28 14:26:47 | ||
图片预览








文档简介
(共23张PPT)
华师大版 初中数学
可化为一元一次方程的分式方程
§16.3
一、创设情境
水流中的速度为3千米/时,它沿江以最大航速顺流航行80千米所用时间与以最大航速逆流航行60千米所用时间相等,轮船在静水中的速度为多少?
解:轮船在静水中的速度为v千米/小时,
顺流航行速度为_________千米/小时,
逆流航行速度为_________千米/小时,
顺流航行80千米所用的时间为__________小时,
逆流航行60千米所用的时间为_________小时.
根据题意,得:
这个方程和我们学过的整式方程有什么不同呢?
这个方程的分母中含有未知数
二、概念导入
分母中含未知数的方程叫做分式方程.
区别
整式方程的未知数不在分母中
分式方程的分母中含有未知数
判一判:下列那些是分式方程 ?
答案: (1),(6)是整式方程, (5)是分式, (2)(3)(4)是分式方程
三、探究新知
怎样解分式方程 呢?
有没有办法去掉分式方程中的分母把它转化为整式方程?
在方程两边都乘以最简公分母(3+v)(v-3),约去分母得,
概括:解分式方程的一般思路
分式方程
整式方程
去分母
两边都乘以最简公分母
例1、解方程
x-1
1
2
=
x2-1
解:在方程两边都乘以最简公分母(x+1)(x-1)得,x+1=2
解这个整式方程,得x=1
把x = 5 代入原分式方程中,发现分母x-1和x2-1的值都为 0,相应的分式无意义,因此x=1虽是方程x+1=2的解, 但不是原分式方程的解.实际上,这个分式方程无解.
分式两边同乘了等于0的式子,所得整式方程的解使分母为0,这个整式方程的解就不是原分式方程的解
上面两个分式方程中,为什么
80
3+V
60
V-3
=
去分母后得到的整式方程的解就是它的解,而
去分母后得到的整式方程的解却不
x-1
1
x2-2
2
=
是原分式方程的解呢?
1
x-1
2
=
x2-1
我们来观察去分母的过程
80
3+V
60
V-3
=
80(v-3)=60(3+v)
x+1=2
两边同乘(3+v)(v-3)
当v=21时,(3+v)(v-3)≠0
两边同乘(x+1)(x-1)
当x=1时, (x+1)(x-1)=0
分式两边同乘了不为0的式子,所得整式方程的解与
分式方程的解相同.
反思与发现
【分式方程解的检验】
解分式方程时,去分母后所得整式方程的解有可能
使原方程的分母为0,所以分式方程的解必须检验.
怎样检验这个整式方程的解是不是原分式方程的解?
将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解,否则这个解就不是原分式方程的解.
例 2
解方程:
解 :方程两边同乘最简公分母 x(x-7),得
100(x-7)=30x
解这个整式方程得
x=10
检验:把x=10代入x(x-3),得
10×(10-7)≠0
∴x=10是原分式方程的解
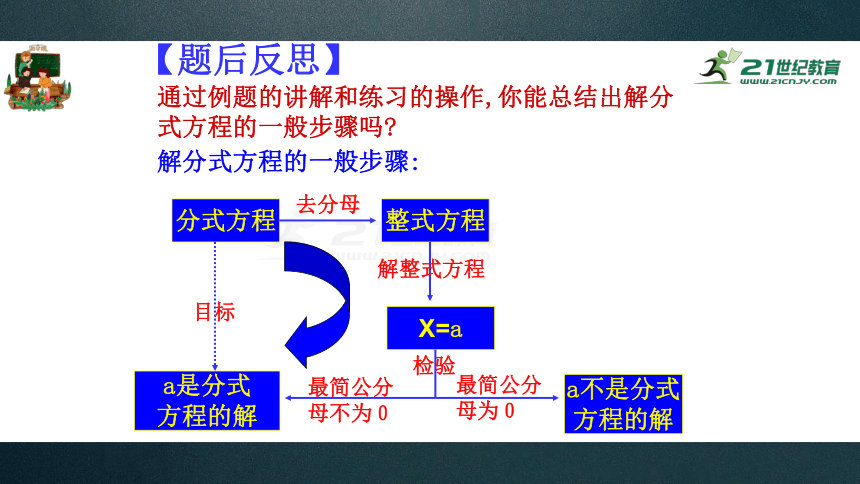
通过例题的讲解和练习的操作,你能总结出解分式方程的一般步骤吗?
解分式方程的一般步骤:
分式方程
整式方程
a是分式
方程的解
X=a
a不是分式
方程的解
去分母
解整式方程
检验
目标
最简公分
母不为0
最简公分
母为0
【题后反思】
练一练
1. 解方程:
解:
方程两边同乘以
检验:把x=5代入 x-4,
得x-4≠0
∴x=5是原方程的解.
(2)
解:方程两边同乘以
检验:把x=-2代入 x2-4,
得x2-4=0。
∴x=-2是增根,从而原方程无解。.
注意:分式方程的求根过程不一定是同解变形,所以分式方程一定要验根!
例3.当a为何值时,方程 有增根?
解:去分母,方程两边同乘以
解这个整式方程,得
因为方程有增根,所以
所以
所以当
时,原方程产生增根.
例5.解关于 的分式方程
解:去分母,方程两边同乘以
移项,得
所以
所以
经检验
是原方程的根.
因为
可化为一元一次方程的分式方程
(第二课时)
§16.3
2、在行程问题中,主要是有三个量---路程、速度、时间。它们的关系是----
路程= 、速度= 、时间= 。
3、在水流行程中:已知静水速度和水流速度
顺水速度= ,
逆水速度= 。
速度×时间
静水速度 + 水流速度
静水速度-水流速度
1、在工程问题中,主要的三个量是:工作量、工作效率、工作时间。它们的关系是
工作量=________________、工作效率=_________
工作时间=_________
工作效率×工作时间
题后小结
4、列一元一次方程解应用题的一般步骤:
1).审:分析题意,找出数量关系和相等关系.
2).设:选择恰当的未知数,注意单位和语言完整.
3).列:根据数量和相等关系,正确列出代数式和方程.
4).解:认真仔细.
5).答:注意单位和语言完整.且答案要生活化.
二、例题解析
某校招生录取时,为了避免数据输入出错, 2640名学生的成绩分别由两位程序操作员各向计算机输入一遍,然后让计算机比较两人的输入是否一致。已知甲的输入速度是乙的2倍,结果甲比乙少用2h输完数据。问:这两位操作员每分钟各能输入多少名学生的成绩 ?
分析:有工作总量2640,求的是工作效率,那么一定是根据工作时间来列等量关系的.关键描述语是:“甲比乙少用2小时输完”.等量关系为:乙用的时间-甲用的时间=2.
解:设乙每分钟输入x名学生成绩,根据题意得:
解得x=11;
经检验x=11是原方程的解.X=11时,2x=22,
则甲每小时输1320名学生成绩;
答:甲每分钟输入22名学生成绩,乙每分钟输入11
名学生成绩
列分式方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:有两次检验.
6.答:注意单位和语言完整.且答案要生活化.
题后小结
两次检验是:
(1)是否是所列方程的解;
(2)是否满足实际意义.
即时练习: 两个工程队共同参与一项筑路工程,甲队单 施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成。哪个队的施工速度快?
工作效率 工作时间 工作量
甲队
乙队
思考:这是____问题,总工作量为____
分析:
等量关系:甲队工作量+乙队工作量=1
工程
1
解:设乙队单独做需x个月完成工程,由题意,得
解得x=1
检验:当x=1时 6x≠0∴x=1是原方程的解
答:乙队施工速度快。
∴乙队单独做1个月完成
∵甲队1个月只做
∴乙队施工速度快
方程两边同乘以6x,得
2x+x+3=6x
学习小结
1、你学到了哪些知识?要注意什么问题?
2、在学习的过程 中你有什么体会?
https://www.21cnjy.com/help/help_extract.php
华师大版 初中数学
可化为一元一次方程的分式方程
§16.3
一、创设情境
水流中的速度为3千米/时,它沿江以最大航速顺流航行80千米所用时间与以最大航速逆流航行60千米所用时间相等,轮船在静水中的速度为多少?
解:轮船在静水中的速度为v千米/小时,
顺流航行速度为_________千米/小时,
逆流航行速度为_________千米/小时,
顺流航行80千米所用的时间为__________小时,
逆流航行60千米所用的时间为_________小时.
根据题意,得:
这个方程和我们学过的整式方程有什么不同呢?
这个方程的分母中含有未知数
二、概念导入
分母中含未知数的方程叫做分式方程.
区别
整式方程的未知数不在分母中
分式方程的分母中含有未知数
判一判:下列那些是分式方程 ?
答案: (1),(6)是整式方程, (5)是分式, (2)(3)(4)是分式方程
三、探究新知
怎样解分式方程 呢?
有没有办法去掉分式方程中的分母把它转化为整式方程?
在方程两边都乘以最简公分母(3+v)(v-3),约去分母得,
概括:解分式方程的一般思路
分式方程
整式方程
去分母
两边都乘以最简公分母
例1、解方程
x-1
1
2
=
x2-1
解:在方程两边都乘以最简公分母(x+1)(x-1)得,x+1=2
解这个整式方程,得x=1
把x = 5 代入原分式方程中,发现分母x-1和x2-1的值都为 0,相应的分式无意义,因此x=1虽是方程x+1=2的解, 但不是原分式方程的解.实际上,这个分式方程无解.
分式两边同乘了等于0的式子,所得整式方程的解使分母为0,这个整式方程的解就不是原分式方程的解
上面两个分式方程中,为什么
80
3+V
60
V-3
=
去分母后得到的整式方程的解就是它的解,而
去分母后得到的整式方程的解却不
x-1
1
x2-2
2
=
是原分式方程的解呢?
1
x-1
2
=
x2-1
我们来观察去分母的过程
80
3+V
60
V-3
=
80(v-3)=60(3+v)
x+1=2
两边同乘(3+v)(v-3)
当v=21时,(3+v)(v-3)≠0
两边同乘(x+1)(x-1)
当x=1时, (x+1)(x-1)=0
分式两边同乘了不为0的式子,所得整式方程的解与
分式方程的解相同.
反思与发现
【分式方程解的检验】
解分式方程时,去分母后所得整式方程的解有可能
使原方程的分母为0,所以分式方程的解必须检验.
怎样检验这个整式方程的解是不是原分式方程的解?
将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解,否则这个解就不是原分式方程的解.
例 2
解方程:
解 :方程两边同乘最简公分母 x(x-7),得
100(x-7)=30x
解这个整式方程得
x=10
检验:把x=10代入x(x-3),得
10×(10-7)≠0
∴x=10是原分式方程的解
通过例题的讲解和练习的操作,你能总结出解分式方程的一般步骤吗?
解分式方程的一般步骤:
分式方程
整式方程
a是分式
方程的解
X=a
a不是分式
方程的解
去分母
解整式方程
检验
目标
最简公分
母不为0
最简公分
母为0
【题后反思】
练一练
1. 解方程:
解:
方程两边同乘以
检验:把x=5代入 x-4,
得x-4≠0
∴x=5是原方程的解.
(2)
解:方程两边同乘以
检验:把x=-2代入 x2-4,
得x2-4=0。
∴x=-2是增根,从而原方程无解。.
注意:分式方程的求根过程不一定是同解变形,所以分式方程一定要验根!
例3.当a为何值时,方程 有增根?
解:去分母,方程两边同乘以
解这个整式方程,得
因为方程有增根,所以
所以
所以当
时,原方程产生增根.
例5.解关于 的分式方程
解:去分母,方程两边同乘以
移项,得
所以
所以
经检验
是原方程的根.
因为
可化为一元一次方程的分式方程
(第二课时)
§16.3
2、在行程问题中,主要是有三个量---路程、速度、时间。它们的关系是----
路程= 、速度= 、时间= 。
3、在水流行程中:已知静水速度和水流速度
顺水速度= ,
逆水速度= 。
速度×时间
静水速度 + 水流速度
静水速度-水流速度
1、在工程问题中,主要的三个量是:工作量、工作效率、工作时间。它们的关系是
工作量=________________、工作效率=_________
工作时间=_________
工作效率×工作时间
题后小结
4、列一元一次方程解应用题的一般步骤:
1).审:分析题意,找出数量关系和相等关系.
2).设:选择恰当的未知数,注意单位和语言完整.
3).列:根据数量和相等关系,正确列出代数式和方程.
4).解:认真仔细.
5).答:注意单位和语言完整.且答案要生活化.
二、例题解析
某校招生录取时,为了避免数据输入出错, 2640名学生的成绩分别由两位程序操作员各向计算机输入一遍,然后让计算机比较两人的输入是否一致。已知甲的输入速度是乙的2倍,结果甲比乙少用2h输完数据。问:这两位操作员每分钟各能输入多少名学生的成绩 ?
分析:有工作总量2640,求的是工作效率,那么一定是根据工作时间来列等量关系的.关键描述语是:“甲比乙少用2小时输完”.等量关系为:乙用的时间-甲用的时间=2.
解:设乙每分钟输入x名学生成绩,根据题意得:
解得x=11;
经检验x=11是原方程的解.X=11时,2x=22,
则甲每小时输1320名学生成绩;
答:甲每分钟输入22名学生成绩,乙每分钟输入11
名学生成绩
列分式方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:认真仔细.
5.验:有两次检验.
6.答:注意单位和语言完整.且答案要生活化.
题后小结
两次检验是:
(1)是否是所列方程的解;
(2)是否满足实际意义.
即时练习: 两个工程队共同参与一项筑路工程,甲队单 施工1个月完成总工程的三分之一,这时增加了乙队,两队又共同工作了半个月,总工程全部完成。哪个队的施工速度快?
工作效率 工作时间 工作量
甲队
乙队
思考:这是____问题,总工作量为____
分析:
等量关系:甲队工作量+乙队工作量=1
工程
1
解:设乙队单独做需x个月完成工程,由题意,得
解得x=1
检验:当x=1时 6x≠0∴x=1是原方程的解
答:乙队施工速度快。
∴乙队单独做1个月完成
∵甲队1个月只做
∴乙队施工速度快
方程两边同乘以6x,得
2x+x+3=6x
学习小结
1、你学到了哪些知识?要注意什么问题?
2、在学习的过程 中你有什么体会?
https://www.21cnjy.com/help/help_extract.php
