北师大版数学必修2第二章第三节《直线与圆的位置关系》专题课件(共53张PPT)
文档属性
| 名称 | 北师大版数学必修2第二章第三节《直线与圆的位置关系》专题课件(共53张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-28 00:00:00 | ||
图片预览










文档简介
(共53张PPT)
专题:直线和圆的位置关系
3.利用直线和圆相离解决的问题?
求圆上一动点到直线距离的最大值和最小值问题
目标要求
1.理解并掌握直线与圆的位置关系:相切、相交、相离
2.会用几何法和方程组法判断直线与圆的位置关系.
3.会求简单的弦长问题、圆的切线方程等问题
特别关注
1.利用几何法和代数法判断直线与圆的位置关系.(重
点)
2.常与方程、不等式等结合命题.(难点)
3.已知直线与圆的位置关系,求相应直线方程时注意斜
率不存在的情形.(易错点)
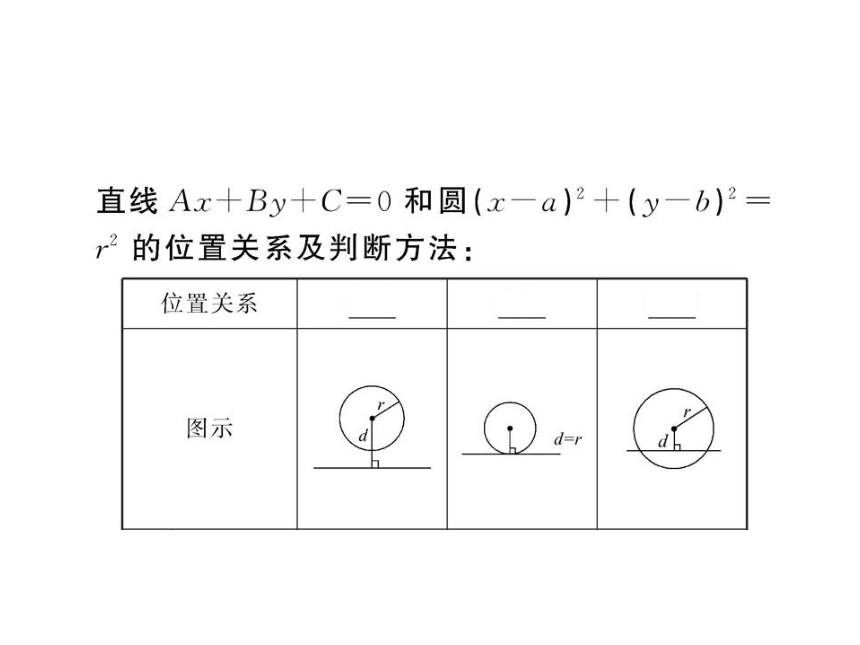
直线Ax+By+C=0和圆(x-a)2+(y-b)2
的位置关系及判断方法:
位置关系
相离
相切
相交
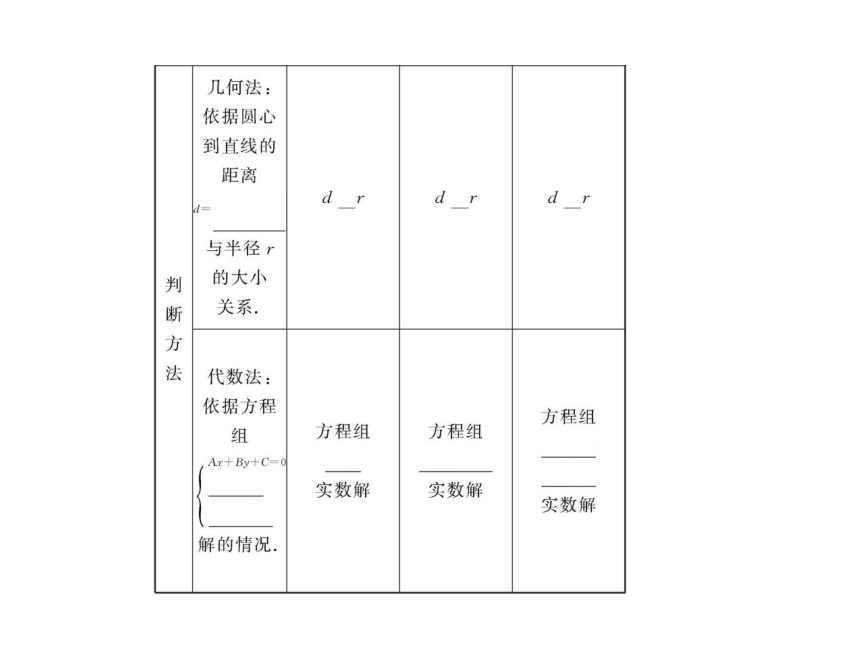
几何法
依据圆心
到直线的
距离
l Aa+Bb+Cl
2+B2
与半径r
判的大小
断关系
方
法代数法:
依据方程
方程组
组
方程组
方程组
有两个
Ax+ By+C
没有
只有一个
实数解
不同的
实数解
实数解
解的情况
想一想:判断直线与圆的位置关系时,代数法与几何法哪
个更方便?
提示:已知直线及圆的方程,判断两者的位置关系时,几
何法较代数法简单,一般情况下,在判断直线与圆的位置
关系时,优先考虑使用几何法
1.利用直线与圆相切可以解决哪些问题?
利用直线与圆相切时,圆心到直线的距离d恰好等于半
径r这一等量关系,我们可以解答有关切线方程、切线
长等问题.
2.利用直线与圆相交可以解决哪些问题?
利用直线与圆相交,可以解决以下常见问题
①弦长问题
②弦心距问题
③求直线方程或圆的方程等问题
类型一
直线与圆位置关系的判定
【例1】判断直线l:y=kx+3与圆O:x2+y2=16的位置关
系
【思路探索】方法一:联立方程组一-消元成二次方程
→判断判别式△的符号→作出结
方法二:求圆心O到直线的距离d→
比较d与半径r的大小→作出结论
方法三:直线恒过定点(0,3)
判断点(0,3)与圆的位置关系→作出结论
+y2=16
自主解答】方法一:由
消去y并整理,得
k x+3
(k2+1)x2+6kx-7=0(兴)
∴△=36k2-4(k2+1)·(-7)
=36k2+28(k2+1)>0,
∴方程()有两个不相等的实根,从而方程组有两组不
同的实数解.故直线l与圆O相交
方法二:设圆心O到直线l的距离为d
≤3<4(圆的半径)
k2+1
故直线l与圆O相交
方法三;依题意,知直线L过定点P(0,3)
02+32<16,
∴点P在圆O内.故直线l与圆O相交
专题:直线和圆的位置关系
3.利用直线和圆相离解决的问题?
求圆上一动点到直线距离的最大值和最小值问题
目标要求
1.理解并掌握直线与圆的位置关系:相切、相交、相离
2.会用几何法和方程组法判断直线与圆的位置关系.
3.会求简单的弦长问题、圆的切线方程等问题
特别关注
1.利用几何法和代数法判断直线与圆的位置关系.(重
点)
2.常与方程、不等式等结合命题.(难点)
3.已知直线与圆的位置关系,求相应直线方程时注意斜
率不存在的情形.(易错点)
直线Ax+By+C=0和圆(x-a)2+(y-b)2
的位置关系及判断方法:
位置关系
相离
相切
相交
几何法
依据圆心
到直线的
距离
l Aa+Bb+Cl
2+B2
与半径r
判的大小
断关系
方
法代数法:
依据方程
方程组
组
方程组
方程组
有两个
Ax+ By+C
没有
只有一个
实数解
不同的
实数解
实数解
解的情况
想一想:判断直线与圆的位置关系时,代数法与几何法哪
个更方便?
提示:已知直线及圆的方程,判断两者的位置关系时,几
何法较代数法简单,一般情况下,在判断直线与圆的位置
关系时,优先考虑使用几何法
1.利用直线与圆相切可以解决哪些问题?
利用直线与圆相切时,圆心到直线的距离d恰好等于半
径r这一等量关系,我们可以解答有关切线方程、切线
长等问题.
2.利用直线与圆相交可以解决哪些问题?
利用直线与圆相交,可以解决以下常见问题
①弦长问题
②弦心距问题
③求直线方程或圆的方程等问题
类型一
直线与圆位置关系的判定
【例1】判断直线l:y=kx+3与圆O:x2+y2=16的位置关
系
【思路探索】方法一:联立方程组一-消元成二次方程
→判断判别式△的符号→作出结
方法二:求圆心O到直线的距离d→
比较d与半径r的大小→作出结论
方法三:直线恒过定点(0,3)
判断点(0,3)与圆的位置关系→作出结论
+y2=16
自主解答】方法一:由
消去y并整理,得
k x+3
(k2+1)x2+6kx-7=0(兴)
∴△=36k2-4(k2+1)·(-7)
=36k2+28(k2+1)>0,
∴方程()有两个不相等的实根,从而方程组有两组不
同的实数解.故直线l与圆O相交
方法二:设圆心O到直线l的距离为d
≤3<4(圆的半径)
k2+1
故直线l与圆O相交
方法三;依题意,知直线L过定点P(0,3)
02+32<16,
∴点P在圆O内.故直线l与圆O相交
