17.1 变量与函数课件(共25张PPT)
文档属性
| 名称 | 17.1 变量与函数课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 18.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-28 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
华师大版 初中数学
第17章 函数及其图象
17.1.1变量与函数
教学目标:
1.了解常量和变量的意义,了解函数的三种表达方式.
2.能根据实际情景列出函数关系式.
重点难点:
1.理解函数概念.
2.学会用函数思想去进行描述、研究其变化规律.
新课引入:
大千世界处在不停的运动变化之中,如何来研究
这些运动变化并寻找规律呢?
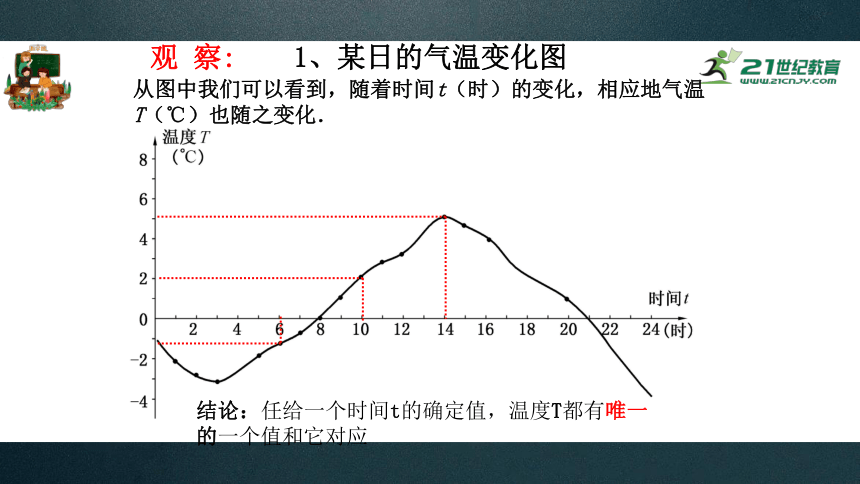
1、某日的气温变化图
从图中我们可以看到,随着时间t(时)的变化,相应地气温T(℃)也随之变化.
观 察:
结论:任给一个时间t的确定值,温度T都有唯一的一个值和它对应
问题2、 2002年7月中国工商银行为“整存整取”的存款方式规定的利率
观察上表,说说随着存期x的增长,
相应的利率y是如何变化的.
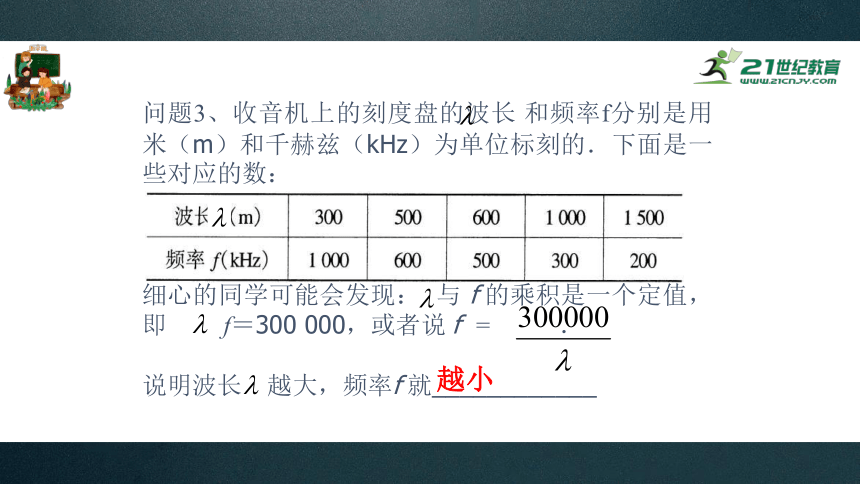
问题3、收音机上的刻度盘的波长 和频率f分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数:
细心的同学可能会发现: 与 f 的乘积是一个定值,即 f=300 000,或者说 f = .
说明波长 越大,频率f 就____________
越小
问题4 圆的面积与半径的关系
圆的面积随着半径的增大而增大.如果用r表示圆的半径,S表示圆的面积。则S与r之间满足下列关系:S=____________.
利用这个关系式,试求出半径为1cm、1.5cm、2cm、2.6cm、3.2cm时圆的面积,并将结果填入下表:
半径r(cm) 1 1.5 2 2.6 3.2 …
圆面积S( cm2 ) …
圆的面积S随着半径r的变化而变化。
在某一变化过程中,可以取不同数值的 量叫做变量(variable).
在问题的研究过程中,还有一种量,它的取值始终保持不变,我们称之为常量
二、概 括
一般地,在一个变化过程中有两个变量x与y,如果对于x的每 一个值,y都有唯一的值与它对应,那么就说x是
自变量,y是因变量,此时也称 y是x的函数。
日常生活和自然界中函数的事例很多:
三、抽象概念
C=2πr
s =60 t
S =(n-2) ×180 0
观察下面关系式
y=x+1
当x=1时,
y=2
y=3
当x=2时,
(2) y2=x
y=4
当x=3时,
y=5
当x=4时,
y随x的变化而变化
当x=1时,
y=+1,-1
y=+2,-2
当x=4时,
y=+3,-3
当x=9时,
y=+4,-4
当x=16时,
关系式(1)y=x+1中对于每个x的值,y都有唯一的值与x对应,y是x的函数
关系式(2)y2=x中对于每个x的值,y有两个不同的值与x对应,y不是x的函数
表示函数关系的方法通常有三种:
?(1)解析法,如观察3中的f= ,观察4中 的S=πr2,这些表达式称为函数的关系式.
?
(2)列表法,如观察2中的利率表,观察3中
的波长与频率关系表.
?
(3) 图象法,观察1中的气温曲线.
华师大版 初中数学
第17章 函数及其图象
17.1.2变量与函数
2、 如果在一个变化过程中,有两个变量,如x和y,对于x的每一个值,y都有唯一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数.
3、函数关系的三种表示方法:
解析法、列表法、图象法
1、在某一变化过程中,可以取不同数值 的量,叫做变量.还有一种量,它的取值始终保持不变,称之为常量.
(1)填写如图所示的加法表,然后把所有填有10的格子涂黑,看看你能发现什么?
如果把这些涂黑的格子横向的加数用x表示,纵向的加数用y表示,试写出y与x的函数关系式.
x
y
(2)试写出等腰三角形中顶角的度数y与底角的度数x之间的函数关系式.并求自变量x的取值范围
y
x
等腰三角形的两底角相等
由于等腰三角形的底角只能是锐角,所以自变量的取值范围是0 (3)如图,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与M重合,让△ABC向右移动,最后点A与点N重合.
问题:
(1)试写出重叠部分面积y(cm2)与线段MA长度x(cm)之间的函数关系式;
(2)当MA=1cm时,重叠部分的面积是多少?
析:(1)根据图形及题意所述可得出重叠部分是等腰直角三角形,从而根据MA的长度可得出y与x的关系;
(2)将x=1cm代入可得出重叠部分的面积.
(1)由题意知,开始时A点与M点重合,让正方形MNPQ向左运动,两图形重合的长度为AM=x,
,0<x≤10,
(2)当MA=1cm时,重叠部分的面积是.
演示
M
Q
N
P
A
B
C
X
X
拓展延伸
如果把题目改为“最后C与N重合,重合的图形面积y与x的关系式会怎样”?请自己动手画画
演示
Q
N
P
A
B
C
X
X-10
M
例、求下列函数中自变量x的取值范围:
(1)y=3x-1;(2)y=2x2+7;
(3)y= (4)y=
(1)(2)中x取任意实数,3x-1都有意义
(3)中,x≠-2时,原式有意义.
(4)中x≥2时,原式有意义.
解:
例题解析
题后反思:
求函数自变量取值范围的两个依据
1、要使函数的解析式有意义
(1)、函数的解析式是整式时 ,自变量可取全体实数。
(2)、函数的解析式分母含有字母时,自变量的取值应使分母不等于零。
(3)、函数解析中自变量作为二次根的被开方数时自变量的取值应使被开方数大于或等于零。
2、对于反映实际问题的函数关系,应使实际问题有意义。
1.求下列函数中自变量x的取值范围(20分)
课堂检测
(1)任意实数
(2)任意实数
(3)x≠-2
2.分别写出下列各问题中的函数关系式及自变量的取值范围:(60分)
(1).某市民用电费标准为每度0.50元,求电费y(元)关于用电度数x的函数关系式;
(2).已知等腰三角形的面积为20cm2,设它的底边长为x(cm),求底边上的高y(cm)关于x的函数关系式;
(3).在一个半径为10 cm的圆形纸片中剪去一个半径为r(cm)的同心圆,得到一个圆环.设圆环的面积为S(cm2),求S关于r的函数关系式.
3.(20分)一架雪橇沿一斜坡滑下,它在时间t(秒)滑下的距离s(米)由下式给出:s=10t+2t2.假如滑到坡底的时间为8秒,试问坡长为多少?
谈谈收获
1、函数关系式的写法;
2、自变量的取值范围.
https://www.21cnjy.com/help/help_extract.php
华师大版 初中数学
第17章 函数及其图象
17.1.1变量与函数
教学目标:
1.了解常量和变量的意义,了解函数的三种表达方式.
2.能根据实际情景列出函数关系式.
重点难点:
1.理解函数概念.
2.学会用函数思想去进行描述、研究其变化规律.
新课引入:
大千世界处在不停的运动变化之中,如何来研究
这些运动变化并寻找规律呢?
1、某日的气温变化图
从图中我们可以看到,随着时间t(时)的变化,相应地气温T(℃)也随之变化.
观 察:
结论:任给一个时间t的确定值,温度T都有唯一的一个值和它对应
问题2、 2002年7月中国工商银行为“整存整取”的存款方式规定的利率
观察上表,说说随着存期x的增长,
相应的利率y是如何变化的.
问题3、收音机上的刻度盘的波长 和频率f分别是用米(m)和千赫兹(kHz)为单位标刻的.下面是一些对应的数:
细心的同学可能会发现: 与 f 的乘积是一个定值,即 f=300 000,或者说 f = .
说明波长 越大,频率f 就____________
越小
问题4 圆的面积与半径的关系
圆的面积随着半径的增大而增大.如果用r表示圆的半径,S表示圆的面积。则S与r之间满足下列关系:S=____________.
利用这个关系式,试求出半径为1cm、1.5cm、2cm、2.6cm、3.2cm时圆的面积,并将结果填入下表:
半径r(cm) 1 1.5 2 2.6 3.2 …
圆面积S( cm2 ) …
圆的面积S随着半径r的变化而变化。
在某一变化过程中,可以取不同数值的 量叫做变量(variable).
在问题的研究过程中,还有一种量,它的取值始终保持不变,我们称之为常量
二、概 括
一般地,在一个变化过程中有两个变量x与y,如果对于x的每 一个值,y都有唯一的值与它对应,那么就说x是
自变量,y是因变量,此时也称 y是x的函数。
日常生活和自然界中函数的事例很多:
三、抽象概念
C=2πr
s =60 t
S =(n-2) ×180 0
观察下面关系式
y=x+1
当x=1时,
y=2
y=3
当x=2时,
(2) y2=x
y=4
当x=3时,
y=5
当x=4时,
y随x的变化而变化
当x=1时,
y=+1,-1
y=+2,-2
当x=4时,
y=+3,-3
当x=9时,
y=+4,-4
当x=16时,
关系式(1)y=x+1中对于每个x的值,y都有唯一的值与x对应,y是x的函数
关系式(2)y2=x中对于每个x的值,y有两个不同的值与x对应,y不是x的函数
表示函数关系的方法通常有三种:
?(1)解析法,如观察3中的f= ,观察4中 的S=πr2,这些表达式称为函数的关系式.
?
(2)列表法,如观察2中的利率表,观察3中
的波长与频率关系表.
?
(3) 图象法,观察1中的气温曲线.
华师大版 初中数学
第17章 函数及其图象
17.1.2变量与函数
2、 如果在一个变化过程中,有两个变量,如x和y,对于x的每一个值,y都有唯一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数.
3、函数关系的三种表示方法:
解析法、列表法、图象法
1、在某一变化过程中,可以取不同数值 的量,叫做变量.还有一种量,它的取值始终保持不变,称之为常量.
(1)填写如图所示的加法表,然后把所有填有10的格子涂黑,看看你能发现什么?
如果把这些涂黑的格子横向的加数用x表示,纵向的加数用y表示,试写出y与x的函数关系式.
x
y
(2)试写出等腰三角形中顶角的度数y与底角的度数x之间的函数关系式.并求自变量x的取值范围
y
x
等腰三角形的两底角相等
由于等腰三角形的底角只能是锐角,所以自变量的取值范围是0
问题:
(1)试写出重叠部分面积y(cm2)与线段MA长度x(cm)之间的函数关系式;
(2)当MA=1cm时,重叠部分的面积是多少?
析:(1)根据图形及题意所述可得出重叠部分是等腰直角三角形,从而根据MA的长度可得出y与x的关系;
(2)将x=1cm代入可得出重叠部分的面积.
(1)由题意知,开始时A点与M点重合,让正方形MNPQ向左运动,两图形重合的长度为AM=x,
,0<x≤10,
(2)当MA=1cm时,重叠部分的面积是.
演示
M
Q
N
P
A
B
C
X
X
拓展延伸
如果把题目改为“最后C与N重合,重合的图形面积y与x的关系式会怎样”?请自己动手画画
演示
Q
N
P
A
B
C
X
X-10
M
例、求下列函数中自变量x的取值范围:
(1)y=3x-1;(2)y=2x2+7;
(3)y= (4)y=
(1)(2)中x取任意实数,3x-1都有意义
(3)中,x≠-2时,原式有意义.
(4)中x≥2时,原式有意义.
解:
例题解析
题后反思:
求函数自变量取值范围的两个依据
1、要使函数的解析式有意义
(1)、函数的解析式是整式时 ,自变量可取全体实数。
(2)、函数的解析式分母含有字母时,自变量的取值应使分母不等于零。
(3)、函数解析中自变量作为二次根的被开方数时自变量的取值应使被开方数大于或等于零。
2、对于反映实际问题的函数关系,应使实际问题有意义。
1.求下列函数中自变量x的取值范围(20分)
课堂检测
(1)任意实数
(2)任意实数
(3)x≠-2
2.分别写出下列各问题中的函数关系式及自变量的取值范围:(60分)
(1).某市民用电费标准为每度0.50元,求电费y(元)关于用电度数x的函数关系式;
(2).已知等腰三角形的面积为20cm2,设它的底边长为x(cm),求底边上的高y(cm)关于x的函数关系式;
(3).在一个半径为10 cm的圆形纸片中剪去一个半径为r(cm)的同心圆,得到一个圆环.设圆环的面积为S(cm2),求S关于r的函数关系式.
3.(20分)一架雪橇沿一斜坡滑下,它在时间t(秒)滑下的距离s(米)由下式给出:s=10t+2t2.假如滑到坡底的时间为8秒,试问坡长为多少?
谈谈收获
1、函数关系式的写法;
2、自变量的取值范围.
https://www.21cnjy.com/help/help_extract.php
