17.3. 1 一次函数课件(共12张PPT)
文档属性
| 名称 | 17.3. 1 一次函数课件(共12张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 18.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-28 14:35:18 | ||
图片预览





文档简介
(共12张PPT)
华师大版 初中数学
17.3. 1 一次函数
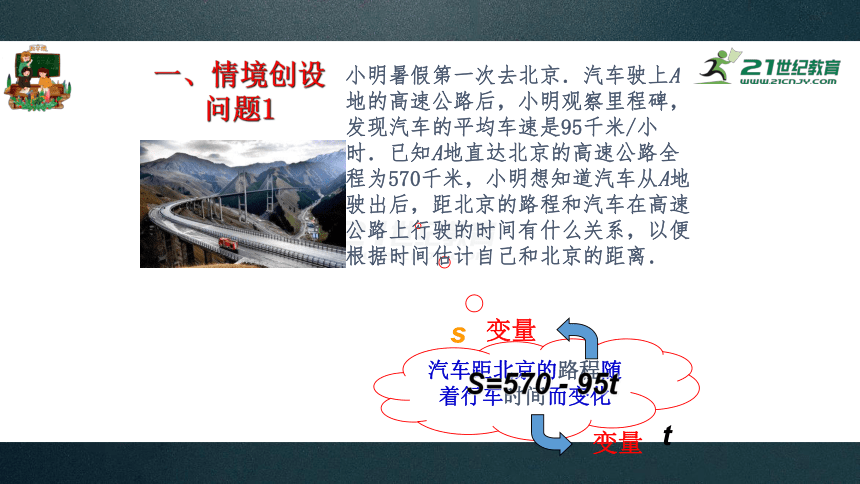
一、情境创设问题1
汽车距北京的路程随着行车时间而变化
小明暑假第一次去北京.汽车驶上A地的高速公路后,小明观察里程碑,发现汽车的平均车速是95千米/小时.已知A地直达北京的高速公路全程为570千米,小明想知道汽车从A地驶出后,距北京的路程和汽车在高速公路上行驶的时间有什么关系,以便根据时间估计自己和北京的距离.
变量
变量
t
s
S=570 - 95t
问题2
弹簧下端悬挂重物,弹簧的长度会伸长,弹簧的长度y(厘米)是所挂重物质量x(千克)的函数,已知一根弹簧在不挂重物时长6厘米,在一定的弹性限度内,每挂1千克重物弹簧伸长0.3厘米,求这个函数关系式。
解:因为每挂1千克重物弹簧伸长0.3厘米,所以挂x千克重物时,弹簧伸长0.3x厘米,又因为不挂重物时弹簧的长度为6厘米,所以挂x厘米重物时弹簧的长度为(0.3x+6)厘米,即有
S=570 - 95t
上述两个问题中的函数解析式都是用自变量的一次整式表示的.我们称它们为一次函数.
一次函数通常可以表示为 的形式,其中k、b是常数,k≠0.
特别地,当 b = 0 时,一次函数 y =kx (常数k≠0)也叫做正比例函数.
二、抽象概括
这两个关系式有什么共同点?
例1 下列函数中,哪些是一次函数?哪些是正比例函数?
二、例题解析
注意化简:
解:(1)(3)(5)是一次函数;
(1)(3)是正比例函数
例2 下列函数关系中,哪些属于一次函数,其中哪些又属于正比例函数?
⑴面积为10cm2的三角形的底a(cm)与这边上的高h(cm);
⑵长为8(cm)的平行四边形的周长L(cm)与宽b(cm);
⑶食堂原有煤120吨,每天要用去5吨,x天后还剩下煤y 吨;
⑷汽车每小时行40千米,行驶的路程s(千米)和时间t(小时).
小结
一次函数、正比例函数以及它们的关系:
函数的解析式都是用自变量的一次整式表示的,我们称它们为一次函数,一次函数通常可以表示为y=kx+b的形式,其中k、b是常数,k≠0.
特别地,当b=0时,一次函数y=kx(常数k≠0)出叫正比例函数.正比例函数也是一次函数,它是一次函数的特例.
方法归纳 :在具体问题中,如果涉及两个变量且只包含一个等量关系时,常用两个字母表示?这两个变量,通过建立函数模型来解决问题. 识别一个具体的函数是否为一次函数或正比例函数的关键是理解一次函数、正?比例函数的意义及能否转化成其一般表达形式.
(1)下列说法不正确的是( )
A一次函数不一定是正比例函数。
B不是一次函数就一定不是正比例函数。
C正比例函数是特殊的一次函数
D不是正比例函数就一定不是一次函数。
(2)下列函数中一次函数的个数为( )
①y=2x;②y=3+4x;③y=1/2;
④y=ax(a≠0的常数);
⑤xy=3;⑥2x+3y-1=0
A.3个 B.4个 C.5个 D.6个
1、选择题(每题10分,共计20分)
检测反馈
D
B
2.(40分)已知y-3与x成正比例,且x=2时,y=7
(1)写出y与x之间的函数关系.
(2)y与x之间是什么函数关系.
(3)计算y=-4时x的值.
解:设y-3=kx (k≠0,k为常数),把x=2时,y =7代入上式,得7-3=2k,K=2,所以y-3=2x
即y=2x+3
(2)y是x的一次函数
(3)把y=-4代入y=2x+3中,得-4=2x+3
x=-3.5
3.(40分)甲市到乙市的包裹邮资为每千克0.9元,每件另加手续费0.2元,求总邮资y(元)与包裹重量x(千克)之间的函数解析式,并计算5千克重的包裹的邮资.
解:
https://www.21cnjy.com/help/help_extract.php
华师大版 初中数学
17.3. 1 一次函数
一、情境创设问题1
汽车距北京的路程随着行车时间而变化
小明暑假第一次去北京.汽车驶上A地的高速公路后,小明观察里程碑,发现汽车的平均车速是95千米/小时.已知A地直达北京的高速公路全程为570千米,小明想知道汽车从A地驶出后,距北京的路程和汽车在高速公路上行驶的时间有什么关系,以便根据时间估计自己和北京的距离.
变量
变量
t
s
S=570 - 95t
问题2
弹簧下端悬挂重物,弹簧的长度会伸长,弹簧的长度y(厘米)是所挂重物质量x(千克)的函数,已知一根弹簧在不挂重物时长6厘米,在一定的弹性限度内,每挂1千克重物弹簧伸长0.3厘米,求这个函数关系式。
解:因为每挂1千克重物弹簧伸长0.3厘米,所以挂x千克重物时,弹簧伸长0.3x厘米,又因为不挂重物时弹簧的长度为6厘米,所以挂x厘米重物时弹簧的长度为(0.3x+6)厘米,即有
S=570 - 95t
上述两个问题中的函数解析式都是用自变量的一次整式表示的.我们称它们为一次函数.
一次函数通常可以表示为 的形式,其中k、b是常数,k≠0.
特别地,当 b = 0 时,一次函数 y =kx (常数k≠0)也叫做正比例函数.
二、抽象概括
这两个关系式有什么共同点?
例1 下列函数中,哪些是一次函数?哪些是正比例函数?
二、例题解析
注意化简:
解:(1)(3)(5)是一次函数;
(1)(3)是正比例函数
例2 下列函数关系中,哪些属于一次函数,其中哪些又属于正比例函数?
⑴面积为10cm2的三角形的底a(cm)与这边上的高h(cm);
⑵长为8(cm)的平行四边形的周长L(cm)与宽b(cm);
⑶食堂原有煤120吨,每天要用去5吨,x天后还剩下煤y 吨;
⑷汽车每小时行40千米,行驶的路程s(千米)和时间t(小时).
小结
一次函数、正比例函数以及它们的关系:
函数的解析式都是用自变量的一次整式表示的,我们称它们为一次函数,一次函数通常可以表示为y=kx+b的形式,其中k、b是常数,k≠0.
特别地,当b=0时,一次函数y=kx(常数k≠0)出叫正比例函数.正比例函数也是一次函数,它是一次函数的特例.
方法归纳 :在具体问题中,如果涉及两个变量且只包含一个等量关系时,常用两个字母表示?这两个变量,通过建立函数模型来解决问题. 识别一个具体的函数是否为一次函数或正比例函数的关键是理解一次函数、正?比例函数的意义及能否转化成其一般表达形式.
(1)下列说法不正确的是( )
A一次函数不一定是正比例函数。
B不是一次函数就一定不是正比例函数。
C正比例函数是特殊的一次函数
D不是正比例函数就一定不是一次函数。
(2)下列函数中一次函数的个数为( )
①y=2x;②y=3+4x;③y=1/2;
④y=ax(a≠0的常数);
⑤xy=3;⑥2x+3y-1=0
A.3个 B.4个 C.5个 D.6个
1、选择题(每题10分,共计20分)
检测反馈
D
B
2.(40分)已知y-3与x成正比例,且x=2时,y=7
(1)写出y与x之间的函数关系.
(2)y与x之间是什么函数关系.
(3)计算y=-4时x的值.
解:设y-3=kx (k≠0,k为常数),把x=2时,y =7代入上式,得7-3=2k,K=2,所以y-3=2x
即y=2x+3
(2)y是x的一次函数
(3)把y=-4代入y=2x+3中,得-4=2x+3
x=-3.5
3.(40分)甲市到乙市的包裹邮资为每千克0.9元,每件另加手续费0.2元,求总邮资y(元)与包裹重量x(千克)之间的函数解析式,并计算5千克重的包裹的邮资.
解:
https://www.21cnjy.com/help/help_extract.php
