第二章 《基本初等函数(I)复习课》21张PPT
文档属性
| 名称 | 第二章 《基本初等函数(I)复习课》21张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-29 11:58:24 | ||
图片预览







文档简介
(共21张PPT)
基本初等函数(1)
复习课
基本初等函数(1)
一、知识梳理
(一)、知识结构:
以同桌两位同学为一小组,
合作画出本章的知识结构图。
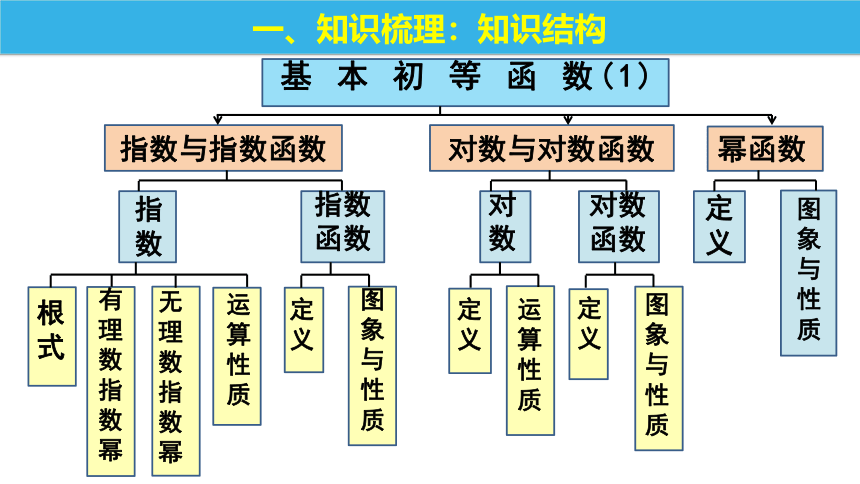
基 本 初 等 函 数(1)
指数与指数函数
对数与对数函数
幂函数
指数
指数函数
对数
对数函数
定义
图象与性质
根
式
有理数指数幂
无理数指数幂
运算性质
定
义
图象与性质
图象与性质
定
义
定
义
运算性质
一、知识梳理:知识结构
一、知识梳理:核心速填
1、根式的性质
一、知识梳理:核心速填
2、有理数指数幂的运算性质
一、知识梳理:核心速填
一、知识梳理:核心速填
一、知识梳理:核心速填
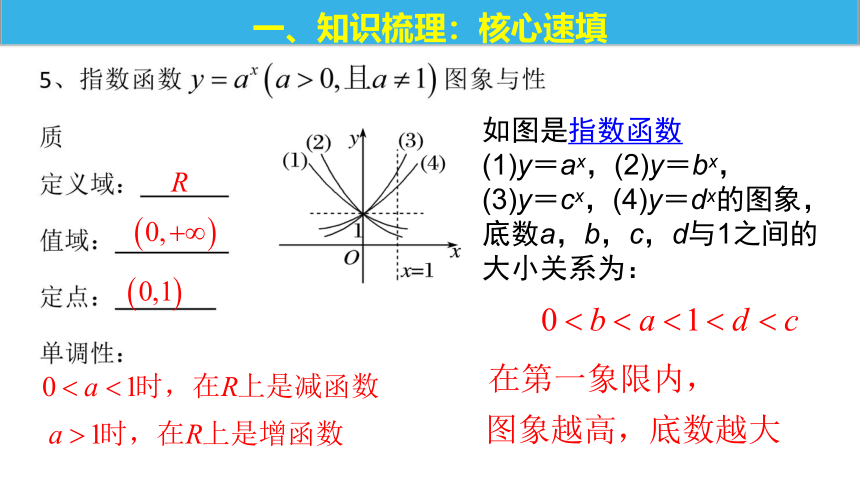
如图是指数函数
(1)y=ax,(2)y=bx,
(3)y=cx,(4)y=dx的图象,
底数a,b,c,d与1之间的
大小关系为:
一、知识梳理:核心速填
如图是四个对数函数的
图象,则底数a,b,c,d
与1之间的大小关系为:
一、知识梳理:核心速填
二、基础自测(复习参考题A、B组P82)
基 本 初 等 函 数(Ⅰ)
知识梳理
基本题型
思想方法
指、对数函数、幂函数的定义图像和性质
指数与对数的运算
大小比较
定义域与值域
图像及应用
性质及应用
综
合
问
题
转化与化归思想
分类讨论思想
函数与方程思想
数形结合思想
构造法
换元
法
配方法
三、深化梳理
四、核心考点 突破练
例1:已知函数
,记
小结:1、比较大小问题是每年高考的必考内容之一;
2、比大小可以直接比较幂值与对数值的大小,也可以以幂值、对数值为自变量的值,结合所给函数的单调性,比较函数值的大小;
四、核心考点 突破练
变式1:已知函数
,记
小结:注意自变量的值要化到同一单调区间内。
四、核心考点 突破练
小结:1、逆向问题:由两个幂值的大小比较,求参数的取值范围;
2、构造法:构造幂函数;
3、注意幂函数的定义域和单调区间;
4、考查函数思想、分类讨论思想。
四、核心考点 突破练
小结:1、构造两个函数,研究函数图象,
利用数形结合求解;
3、考查函数思想、数形结合思想、分类讨论思想
2、数形结合是解决方程、不等式的重要工具;
四、核心考点 突破练
五、课堂小结
2、基本初等函数与不等式的交汇问题是高考的热点问题,
突破此类问题的关键在于准确把握函数的图象和性质,
利用性质特别是单调性,再结合函数图象寻求突破点。
1、本节课我们的重点是梳理本章知识,归纳总结重点题型及方法,形成知识网络。
3、学会求解与指数函数、对数函数、幂函数有关的复合函数的定义域、解析式、值域、最值、单调性、奇偶性等问题。
六、课后作业
P83页复习参考题B组
第1、4、5、6题.
谢 谢 观 看
基本初等函数(1)
复习课
基本初等函数(1)
一、知识梳理
(一)、知识结构:
以同桌两位同学为一小组,
合作画出本章的知识结构图。
基 本 初 等 函 数(1)
指数与指数函数
对数与对数函数
幂函数
指数
指数函数
对数
对数函数
定义
图象与性质
根
式
有理数指数幂
无理数指数幂
运算性质
定
义
图象与性质
图象与性质
定
义
定
义
运算性质
一、知识梳理:知识结构
一、知识梳理:核心速填
1、根式的性质
一、知识梳理:核心速填
2、有理数指数幂的运算性质
一、知识梳理:核心速填
一、知识梳理:核心速填
一、知识梳理:核心速填
如图是指数函数
(1)y=ax,(2)y=bx,
(3)y=cx,(4)y=dx的图象,
底数a,b,c,d与1之间的
大小关系为:
一、知识梳理:核心速填
如图是四个对数函数的
图象,则底数a,b,c,d
与1之间的大小关系为:
一、知识梳理:核心速填
二、基础自测(复习参考题A、B组P82)
基 本 初 等 函 数(Ⅰ)
知识梳理
基本题型
思想方法
指、对数函数、幂函数的定义图像和性质
指数与对数的运算
大小比较
定义域与值域
图像及应用
性质及应用
综
合
问
题
转化与化归思想
分类讨论思想
函数与方程思想
数形结合思想
构造法
换元
法
配方法
三、深化梳理
四、核心考点 突破练
例1:已知函数
,记
小结:1、比较大小问题是每年高考的必考内容之一;
2、比大小可以直接比较幂值与对数值的大小,也可以以幂值、对数值为自变量的值,结合所给函数的单调性,比较函数值的大小;
四、核心考点 突破练
变式1:已知函数
,记
小结:注意自变量的值要化到同一单调区间内。
四、核心考点 突破练
小结:1、逆向问题:由两个幂值的大小比较,求参数的取值范围;
2、构造法:构造幂函数;
3、注意幂函数的定义域和单调区间;
4、考查函数思想、分类讨论思想。
四、核心考点 突破练
小结:1、构造两个函数,研究函数图象,
利用数形结合求解;
3、考查函数思想、数形结合思想、分类讨论思想
2、数形结合是解决方程、不等式的重要工具;
四、核心考点 突破练
五、课堂小结
2、基本初等函数与不等式的交汇问题是高考的热点问题,
突破此类问题的关键在于准确把握函数的图象和性质,
利用性质特别是单调性,再结合函数图象寻求突破点。
1、本节课我们的重点是梳理本章知识,归纳总结重点题型及方法,形成知识网络。
3、学会求解与指数函数、对数函数、幂函数有关的复合函数的定义域、解析式、值域、最值、单调性、奇偶性等问题。
六、课后作业
P83页复习参考题B组
第1、4、5、6题.
谢 谢 观 看
