排列

(共13张PPT)
1、分类计数原理（加法原理）
2、分步计数原理（乘法原理）
完成一件事，有n类办法,在第1类办法中有m1种不同的方法,在第2类办法中有m2种不同的方法，……，在第n类办法中有mn种不同的方法。那么完成这件事共有
N=m1+m2+…+mn
种不同的方法。
一、复习
完成一件事，需要分成n个步骤，做第1步有m1种不同的方法，做第2步有m2种不同的方法，……，做第n步有mn种不同的方法。那么完成这件事共有
N=m1×m2×…×mn
种不同的方法。
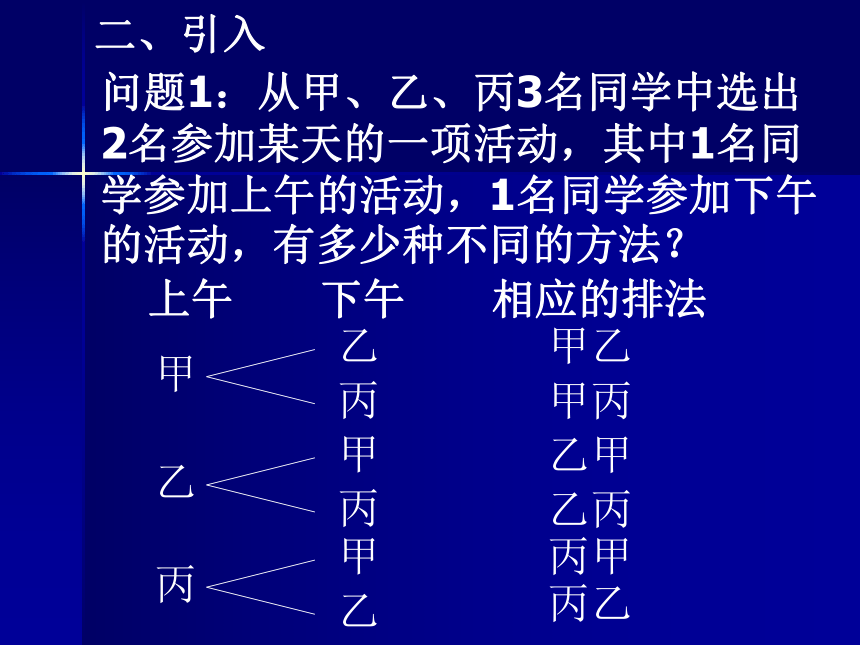
上午 下午 相应的排法
二、引入
问题1：从甲、乙、丙3名同学中选出2名参加某天的一项活动，其中1名同学参加上午的活动，1名同学参加下午的活动，有多少种不同的方法？
乙
丙
甲
乙
丙
甲
丙
甲
乙
甲乙
甲丙
乙甲
乙丙
丙甲
丙乙
问题2：从a，b，c，d这4个字母中，每次取出3个按顺序排成一列，共有多少种不同的排法？
a
b
c
d
c
d
b
d
c
b
b
a
c
d
c
d
a
d
c
a
c
a
b
d
b
d
a
d
b
a
d
a
b
c
b
c
a
c
b
a
abcabdacbacdadbadc
bacbadbcabcdbdabdc
cabcadcbacbdcdacdb
dabdacdbadbcdcadcb
课题：排 列
三、新授
1、排列的定义
从n个不同元素中取出m(m≤n)个元素的所有排列的个数，叫做从n个不同元素中取出m个元素的排列数，用符号 表示。
一般地，从n个不同元素中取出m(m≤n)个元素，按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列。
2、排列数的定义
3、排列数公式
问题：从n个不同元素中取出2个元素的排列数 是多少？
第1位
第2位
n
n-1
n×(n-1)
第1位
第2位
第3位
n
n-1
n-2
……
第1位
第2位
第3位
第m位
n
n-1
n-2
n-m+1
排列数公式，其中
若 ，则有
记为：
（正整数1到n的连乘积）
排列数公式：
四、例题分析
例1、计算
2、
用排列数符号可表示为？
思考1、
若 ，
则
，则
例2、求证：
例3、求和：
五、小结
1、排列的概念要抓住其含的两层意思：（1）取出元素，（2）按一定顺序排列。
2、排列数公式要抓住其特点。
六、布置作业