排序

(共24张PPT)
基本算法：排序
排序
定义：整理文件中的记录，使之按关键字递增(或递减)
次序排列起来。其确切定义如下：
输入：n个记录R1，R2，…，Rn，其相应的关键字分别
为K1，K2，…，Kn。
输出：Ri1，Ri2，…，Rin，使得Ki1≤Ki2≤…≤Kin。(或Ki1≥Ki2≥…≥Kin)。
基本算法：排序
排序的稳定性
当待排序记录的关键字均不相同时，排序结果是唯一的，否则排序结果不唯一。
在待排序的文件中，若存在多个关键字相同的记录，经过排序后这些具有相同关键字的记录之间的相对次序保持不变，该排序方法是稳定的；若具有相同关键字的记录之间的相对次序发生变化，则称这种排序方法是不稳定的。
排序的稳定性
输入序列：49 38 65 97 76 13 27 49
输出序列：13 27 38 49 49 65 76 97
稳定
输出序列：13 27 38 49 49 65 76 97
不稳定
直接插入排序
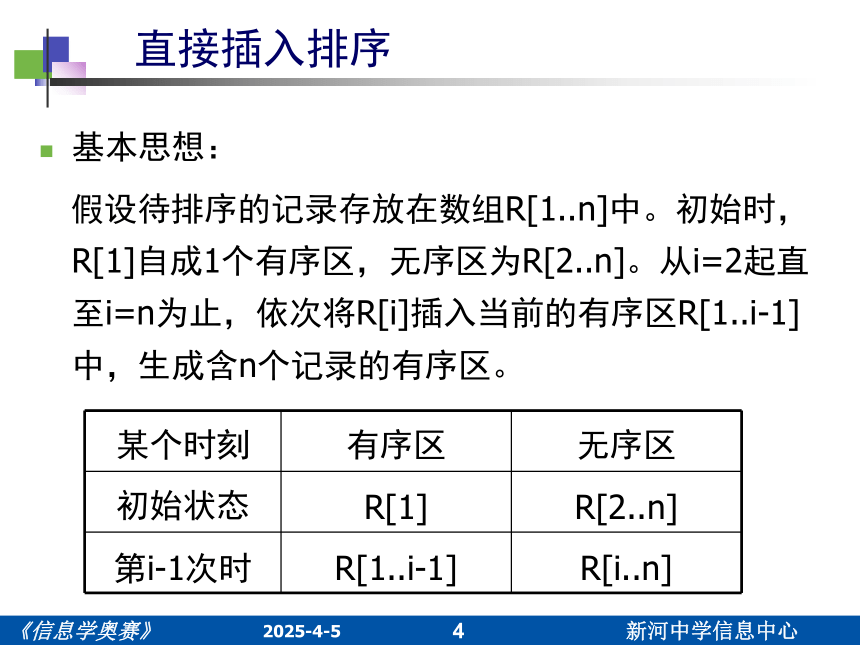
基本思想：
假设待排序的记录存放在数组R[1..n]中。初始时，R[1]自成1个有序区，无序区为R[2..n]。从i=2起直至i=n为止，依次将R[i]插入当前的有序区R[1..i-1]中，生成含n个记录的有序区。
某个时刻 有序区 无序区
初始状态 R[1] R[2..n]
第i-1次时 R[1..i-1] R[i..n]
直接插入排序
第i-1趟直接插入排序
通常将一个记录R[i](i=2，3，…，n-1)插入到当前的有序区，使得插入后仍保证该区间里的记录是按关键字有序的操作。
排序过程的某一中间时刻，R被划分成两个子区间R[1..i-1]（已排好序的有序区）和R[i..n]（当前未排序的部分，可称无序区）。
初始状态： [ 49 ] [ 38 65 97 76 13 27 49 ]
第 1 趟： [ 38 49 ] [ 65 97 76 13 27 49 ]
第 2 趟： [ 38 49 65 ] [ 97 76 13 27 49 ]
第 3 趟： [ 38 49 65 97 ] [ 76 13 27 49 ]
第 4 趟： [ 38 49 65 76 97 ] [ 13 27 49 ]
第 5 趟： [ 13 38 49 65 76 97 ] [ 27 49 ]
输入序列：49 38 65 97 76 13 27 49
第 6 趟： [ 13 27 38 49 65 76 97 ] [ 49 ]
第 7 趟： [ 13 27 38 49 49 65 76 97 ]
直接插入排序算法：
Procedure insertsort(R:array [0..n] of integer);
Var i, j:integer;
Begin
for i:=2 to n do
if R[i]then begin
R[0]:=R[i]; // 哨兵
j:=i-1;
REPEAT
R[j+1]:=R[j];
j:=j-1
Until R[0]>=R[j];
R[j+1]:=R[0]
end;
End;
R[0] R[1..i-1] R[i..n]
直接插入排序
算法分析：
对于n个记录，进行n-1趟排序
直接插入排序是稳定的
最好时间复杂O(n)，比较n-1次，移动0次
最坏时间复杂度O(n2)，比较(n+2)(n-1)/2次
平均时间复杂度O(n2)
冒泡排序
基本思想：
依次比较相邻记录的关键字，发现两个记录的次序相反时即进行交换，直到没有反序的记录为止。
初始状态
R[1]
R[2]
…
…
R[n]
输入序列：49 38 65 97 76 13 27 49
初始
49
38
65
97
76
13
27
49
（1）
13
49
38
65
97
76
27
49
（2）
13
27
49
38
65
97
76
49
（3）
13
27
38
49
49
65
97
76
（4）
13
27
38
49
49
65
76
97
（5）
13
27
38
49
49
65
76
97
（6）
13
27
38
49
49
65
76
97
（7）
13
27
38
49
49
65
76
97
冒泡排序算法：
Procedure bubblesort (R:array [1..n] of integer);
Var i, j:integer;
Begin
for i:=1 to n-1 do
for j:=1 to n-i do
if a[j]then begin
temp:=a[j];
a[j]:=a[j+1];
a[j+1]:=temp
end;
End.
冒泡排序
算法分析：
对于n个记录，进行n-1趟排序
冒泡排序是稳定的
最好时间复杂O(n)，比较n-1次，移动0次
最坏时间复杂度O(n2)，比较n(n-1)/2次
平均时间复杂度O(n2)
快速排序
基本思想：
从n个数据中任意找出一个数（如R[1]）作为基准数（x），利用依次比较、交换，把这n个数分成大于基准（>x）和小于基准（初始状态： [ 49 38 65 97 76 13 27 49 ]
快速排序
i
j
j向左扫描： [ 49 38 65 97 76 13 27 49 ]
第1次交换： [ 27 38 65 97 76 13 49 ]
i向右扫描： [ 27 38 65 97 76 13 49 ]
第2次交换： [ 27 38 97 76 13 65 49 ]
第3次交换： [ 27 38 13 97 76 65 49 ]
第4次交换： [ 27 38 13 76 97 65 49 ]
快速排序算法：
Procedure quicksort(VAR R:array [1..n] of integer;low,high:integer);
Var i, j:integer; x:integer;
Begin
if lowbegin
i:=low; j:=high; x:=a[i];
REPEAT
while (a[j]>=x) and (iif (a[j]while (a[i]<=x) and (iif (a[i]>x) and (iUntil i=j;
a[i]:=x;
quicksort(R, low, i-1); quicksort(R, i+1, high);
end;
End.
快速排序
算法分析：
快速排序是不稳定的
最好时间复杂O(nlog2n)
最坏时间复杂度O(n2)，比较n(n-1)/2次
平均时间复杂度O(nlog2n)
归并排序
基本思想：
利用“归并”技术来进行排序。归并是指将若干个已排序的子文件合并成一个有序的文件。
实现方法：自底向上和自顶向下
采用分治法进行自顶向下的算法设计，形式更为简洁。
归并排序
分治法的三个步骤： 设归并排序的当前区间是R[low..high]
①分解：将当前区间一分为二，即求分裂点 mid=(low+high) div 2；
②求解：递归地对两个子区间R[low..mid]和R[mid+1..high]进行归并排序；
③组合：将已排序的两个子区间R[low..mid]和R[mid+1..high]归并为一个有序的区间R[low..high]。
递归的终结条件：子区间长度为1（一个记录自然有序）
[25 57 48 37 12 92 86]
归并排序
[25 57 48 37] [12 92 86]
[25 57] [48 37] [12 92] [86]
[25][57] [48][37] [12][92]
[25 57] [37 48] [12 92] [86]
[25 37 57 48] [12 86 92]
[12 25 37 48 57 86 92]
归并排序算法：
Procedure mergesort (low, high:integer);
Var mid:integer;
Begin
if (low>=high) then exit;
mid:=(low+high) div 2;
mergesort(low,mid);
mergesort(mid+1,high);
Merge(low,mid,high)
End.
归并排序算法：
mergesort(1,7)
mid=4
mergesort(1,4)
mergesort(5,7)
Merge(1,4,7)
mid=2
mergesort(1,2)
mergesort(3,4)
Merge(1,2,4)
mid=6
mergesort(5,6)
mergesort(7)
Merge(5,6,7)
mid=1
mergesort(1,1)
mergesort(2,2)
Merge(1,1,2)
mid=3
mergesort(3,3)
mergesort(4,4)
Merge(3,3,4)
mid=5
mergesort(5,5)
mergesort(6,6)
Merge(5,5,6)
归并排序算法：
Procedure Merge (low, m, high:integer);
Var i, j, p:integer;
Begin
i:=low; j:=m+1;
for p:=low to high do
if (j>high) or (i<=m) and (R[i]<=R[j])
then begin R1[p]:=R[i]; Inc(i); end
else begin R1[p]:=R[j]; Inc(i); end;
for p:=low to high do
R[p]:=R1[p]
End.
归并排序
算法分析：
归并排序是稳定的
最好时间复杂O(nlog2n)
最坏时间复杂度O(nlog2n)
平均时间复杂度O(nlog2n)