树
图片预览


文档简介
(共26张PPT)
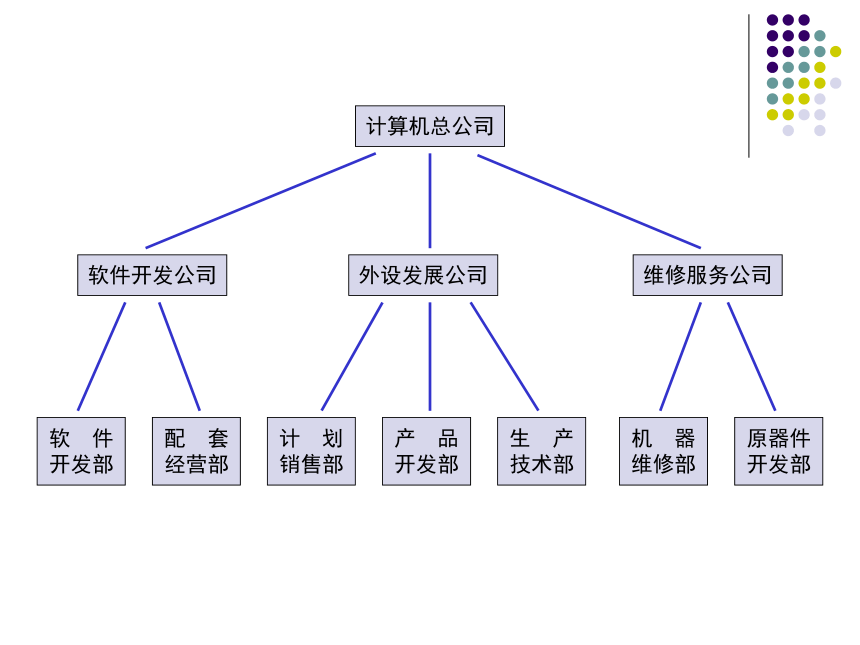
计算机总公司
软件开发公司
外设发展公司
维修服务公司
软 件
开发部
配 套
经营部
计 划
销售部
产 品
开发部
生 产
技术部
机 器
维修部
原器件
开发部
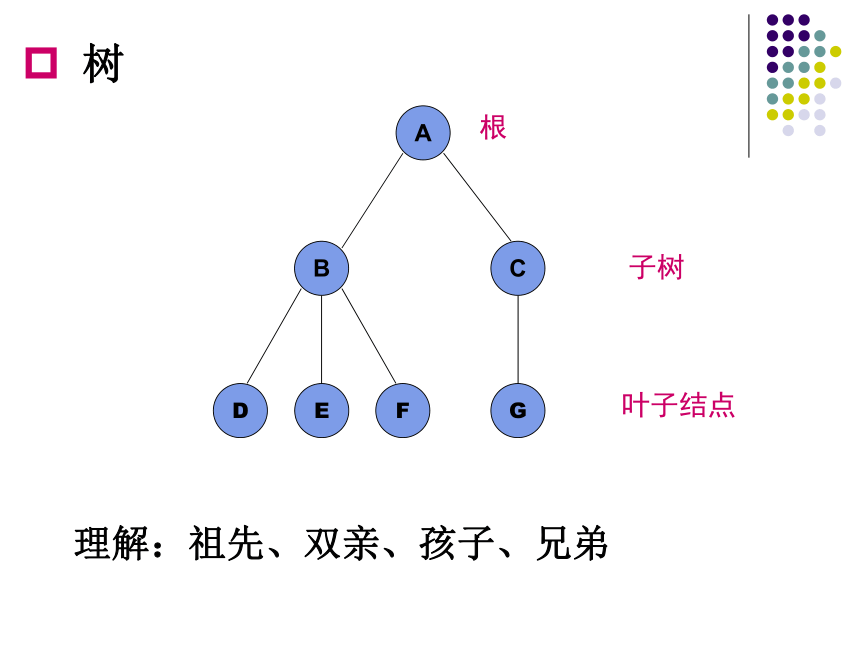
树
A
B
C
D
E
F
G
根
子树
叶子结点
理解:祖先、双亲、孩子、兄弟
树(Tree)——非线性结构
递归定义:
树是n(n≥0)个结点的有限集T,T为空时称为空树,否则它满足两个条件:
(1)有且仅有一个特定的称为根(Root)结点;
(2)其余的结点可分为m(m≥0)个互不相交的子集T1,T2,…,Tm,其中每个子集本身又是一棵树,称其为根的子树(subtree)。
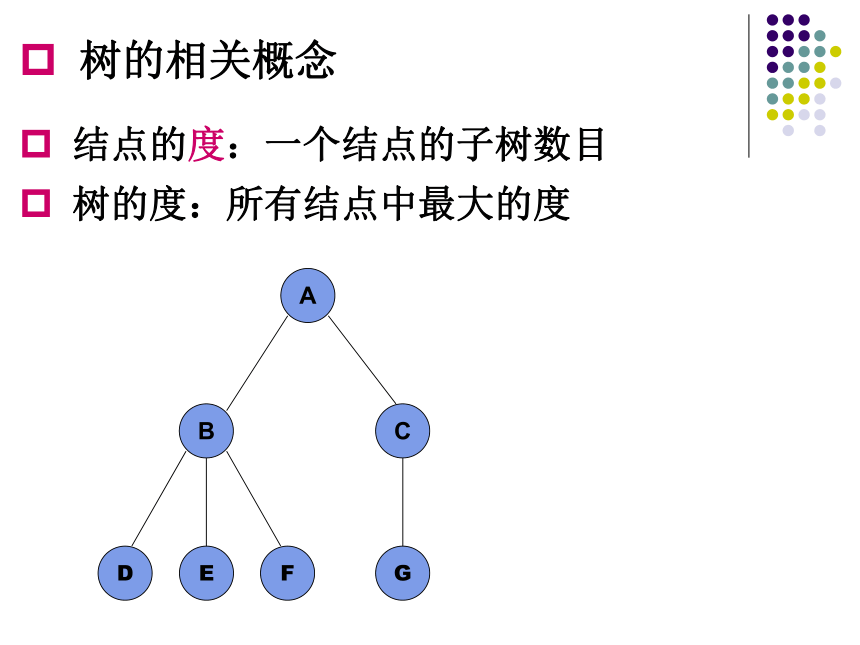
树的相关概念
结点的度:一个结点的子树数目
树的度:所有结点中最大的度
A
B
C
D
E
F
G
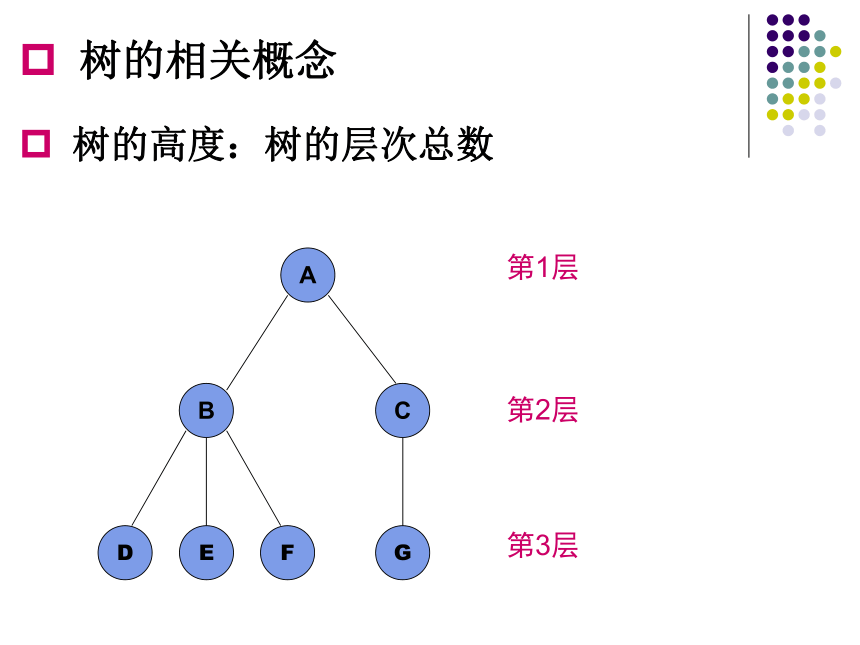
树的相关概念
树的高度:树的层次总数
A
B
C
D
E
F
G
第1层
第2层
第3层
练习:
设树T的高度为4,其中度为1、2、3和4的结点个数分别为4、2、1、1,则T中的叶子数为( )
A. 5 B. 6 C. 7 D. 8
D
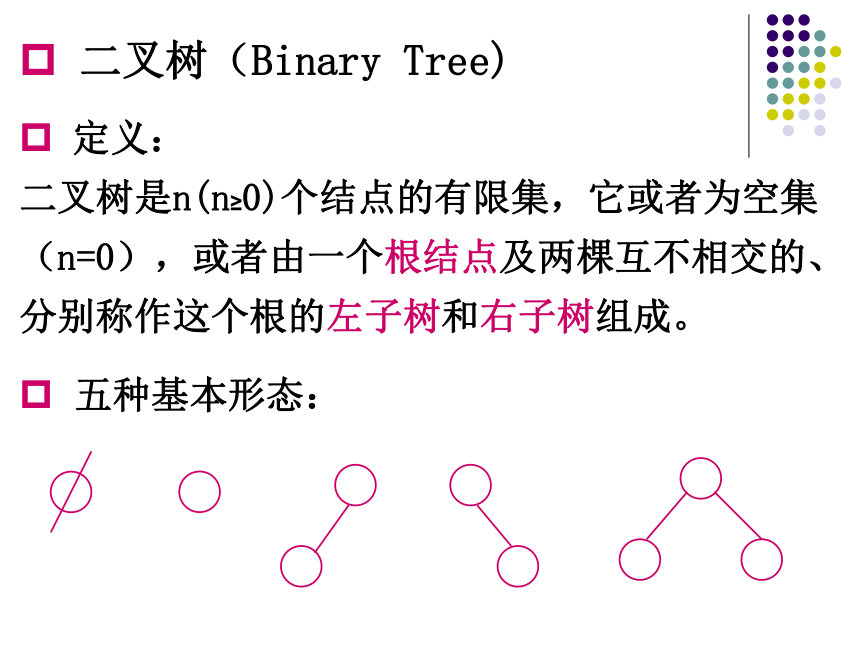
二叉树(Binary Tree)
定义:
二叉树是n(n≥0)个结点的有限集,它或者为空集(n=0),或者由一个根结点及两棵互不相交的、分别称作这个根的左子树和右子树组成。
五种基本形态:
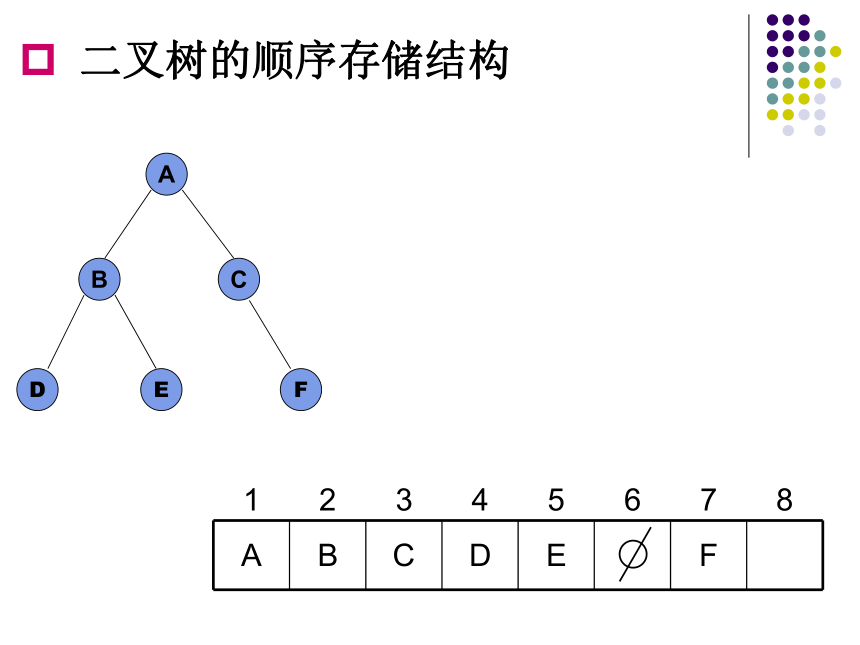
二叉树的顺序存储结构
A
B
C
D
E
F
A B C D E F
1 2 3 4 5 6 7 8
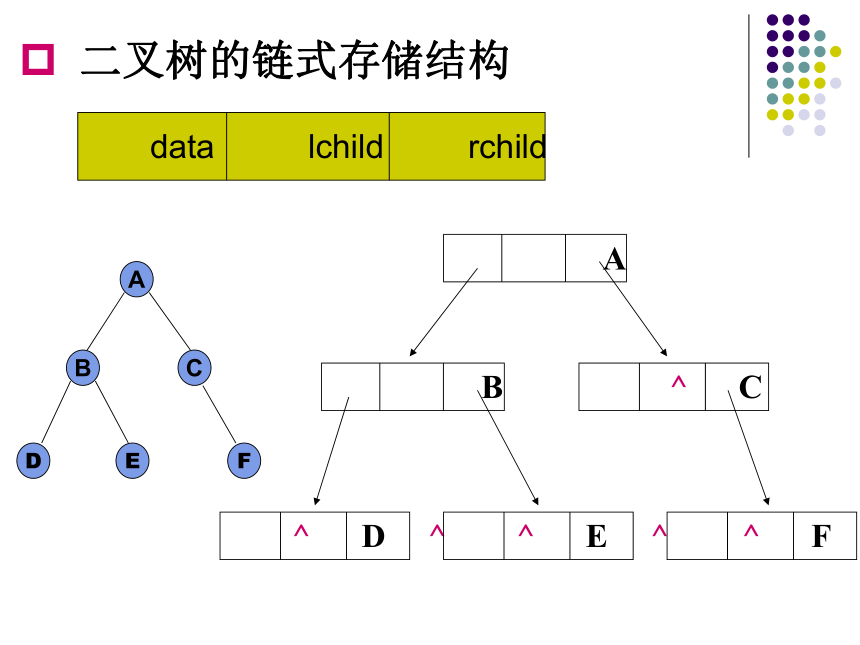
二叉树的链式存储结构
data lchild rchild
A
B
C
D
E
F
A
B
^ C
^ D ^
^ E ^
^ F ^
二叉树的性质
性质1 二叉树第i层上的结点数目最多为
(i≥1)
满二叉树
完全二叉树
2i-1
20
21
22
23
二叉树的性质
性质2 深度为k的二叉树至多有 个结点
(k≥1)
2k-1
满二叉树
完全二叉树
二叉树的性质
性质3 在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1
证明:设结点总数为n,则n=n0+n1+n2 ①
1度结点有一个孩子,2度结点有两个孩子,孩子结点总数有n1+2n2,根结点1个,则n=n1+2n2+1 ②
由①②得,n0+n1+n2=n1+2n2+1 n0=n2+1
练习:
满二叉树的叶子结点个数为N,则它的结点总数为( )。
A. N B. 2N C. 2N – 1 D. 2N + 1
C
练习:
一棵完全二叉树上有1001个结点,其中叶子结点的个数是( )
A. 250 B. 500 C. 254 D. 501
D
二叉树的性质
完全二叉树
性质4 具有n个结点的完全二叉树的深度k为
设n=12,3lg12 = 3,k=3+1=4
lgn + 1
二叉树的遍历
A
B
C
D
E
F
遍历:
指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。
遍历方案(6种):
(1)访问根结点(N);
(2)遍历左子树(L);
(3)遍历右子树(R)。
二叉树的遍历
A
B
C
D
E
F
三种遍历:
(1)前序遍历(先序遍历)
NLR 根-左-右
(2)中序遍历
LNR 左-根-右
(3)后序遍历
LRN 左-右-根
练习:
二叉树T,已知其前序遍历序列为1 2 4 3 5 7 6,中序遍历序列为4 2 1 5 7 3 6,则其后序遍历序列为( )。
A. 4 2 5 7 6 3 1 B. 4 2 7 5 6 3 1 C. 4 2 7 5 3 6 1 D. 4 7 2 3 5 6 1 E. 4 5 2 6 3 7 1
B
练习:
某二叉树中序序列为abcdefg,后序序列为bdcafge,则前序序列是( )
A. egfacbd B. eacbdgf
C. eagcfbd D. 以上答案都不对
B
问题解答:
已知:按中序遍历二叉树的结果为abc。
问:有多少种不同形态的二叉树可以得到这一遍历结果,并画出这些二叉树。
a
b
c
a
c
b
b
a
c
a
b
c
a
b
c
①
③
②
④
⑤
树的路径长度:
从树根到树中每一结点的路径长度之和。
A
B
C
结点数目相同的二叉树,完全二叉树的路径长度最短。
A
B
C
A
B
C
树的带权路径长度(WPL)
结点的带权路径长度:结点到树根之间的路径长度与该结点上权的乘积。
树的带权路径长度:树中所有叶子结点的带权路径长度之和。
最优二叉树(哈夫曼树)
带权路径长度最小的二叉树。
A
B
C
D
假定有四个叶子结点 ,权值分别是7、5、2、4,如何构造哈夫曼树?
C
A
B
D
A
D
B
C
C
A
B
D
WPL=7*2+5*2+2*2+4*2=36
WPL=7*3+5*3+2*1+4*2=46
WPL=7*1+5*2+2*3+4*3=35
例:有五个结点k1,k2,k3,k4,k5,权值分别是16、2、18、16、23,如何构造哈夫曼树?
哈夫曼树
C
A
B
D
若有N个叶子结点,
则结点总数为?
2*N+1
计算机总公司
软件开发公司
外设发展公司
维修服务公司
软 件
开发部
配 套
经营部
计 划
销售部
产 品
开发部
生 产
技术部
机 器
维修部
原器件
开发部
树
A
B
C
D
E
F
G
根
子树
叶子结点
理解:祖先、双亲、孩子、兄弟
树(Tree)——非线性结构
递归定义:
树是n(n≥0)个结点的有限集T,T为空时称为空树,否则它满足两个条件:
(1)有且仅有一个特定的称为根(Root)结点;
(2)其余的结点可分为m(m≥0)个互不相交的子集T1,T2,…,Tm,其中每个子集本身又是一棵树,称其为根的子树(subtree)。
树的相关概念
结点的度:一个结点的子树数目
树的度:所有结点中最大的度
A
B
C
D
E
F
G
树的相关概念
树的高度:树的层次总数
A
B
C
D
E
F
G
第1层
第2层
第3层
练习:
设树T的高度为4,其中度为1、2、3和4的结点个数分别为4、2、1、1,则T中的叶子数为( )
A. 5 B. 6 C. 7 D. 8
D
二叉树(Binary Tree)
定义:
二叉树是n(n≥0)个结点的有限集,它或者为空集(n=0),或者由一个根结点及两棵互不相交的、分别称作这个根的左子树和右子树组成。
五种基本形态:
二叉树的顺序存储结构
A
B
C
D
E
F
A B C D E F
1 2 3 4 5 6 7 8
二叉树的链式存储结构
data lchild rchild
A
B
C
D
E
F
A
B
^ C
^ D ^
^ E ^
^ F ^
二叉树的性质
性质1 二叉树第i层上的结点数目最多为
(i≥1)
满二叉树
完全二叉树
2i-1
20
21
22
23
二叉树的性质
性质2 深度为k的二叉树至多有 个结点
(k≥1)
2k-1
满二叉树
完全二叉树
二叉树的性质
性质3 在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1
证明:设结点总数为n,则n=n0+n1+n2 ①
1度结点有一个孩子,2度结点有两个孩子,孩子结点总数有n1+2n2,根结点1个,则n=n1+2n2+1 ②
由①②得,n0+n1+n2=n1+2n2+1 n0=n2+1
练习:
满二叉树的叶子结点个数为N,则它的结点总数为( )。
A. N B. 2N C. 2N – 1 D. 2N + 1
C
练习:
一棵完全二叉树上有1001个结点,其中叶子结点的个数是( )
A. 250 B. 500 C. 254 D. 501
D
二叉树的性质
完全二叉树
性质4 具有n个结点的完全二叉树的深度k为
设n=12,3
lgn + 1
二叉树的遍历
A
B
C
D
E
F
遍历:
指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。
遍历方案(6种):
(1)访问根结点(N);
(2)遍历左子树(L);
(3)遍历右子树(R)。
二叉树的遍历
A
B
C
D
E
F
三种遍历:
(1)前序遍历(先序遍历)
NLR 根-左-右
(2)中序遍历
LNR 左-根-右
(3)后序遍历
LRN 左-右-根
练习:
二叉树T,已知其前序遍历序列为1 2 4 3 5 7 6,中序遍历序列为4 2 1 5 7 3 6,则其后序遍历序列为( )。
A. 4 2 5 7 6 3 1 B. 4 2 7 5 6 3 1 C. 4 2 7 5 3 6 1 D. 4 7 2 3 5 6 1 E. 4 5 2 6 3 7 1
B
练习:
某二叉树中序序列为abcdefg,后序序列为bdcafge,则前序序列是( )
A. egfacbd B. eacbdgf
C. eagcfbd D. 以上答案都不对
B
问题解答:
已知:按中序遍历二叉树的结果为abc。
问:有多少种不同形态的二叉树可以得到这一遍历结果,并画出这些二叉树。
a
b
c
a
c
b
b
a
c
a
b
c
a
b
c
①
③
②
④
⑤
树的路径长度:
从树根到树中每一结点的路径长度之和。
A
B
C
结点数目相同的二叉树,完全二叉树的路径长度最短。
A
B
C
A
B
C
树的带权路径长度(WPL)
结点的带权路径长度:结点到树根之间的路径长度与该结点上权的乘积。
树的带权路径长度:树中所有叶子结点的带权路径长度之和。
最优二叉树(哈夫曼树)
带权路径长度最小的二叉树。
A
B
C
D
假定有四个叶子结点 ,权值分别是7、5、2、4,如何构造哈夫曼树?
C
A
B
D
A
D
B
C
C
A
B
D
WPL=7*2+5*2+2*2+4*2=36
WPL=7*3+5*3+2*1+4*2=46
WPL=7*1+5*2+2*3+4*3=35
例:有五个结点k1,k2,k3,k4,k5,权值分别是16、2、18、16、23,如何构造哈夫曼树?
哈夫曼树
C
A
B
D
若有N个叶子结点,
则结点总数为?
2*N+1
同课章节目录
