数学运算

(共14张PPT)
数学运算
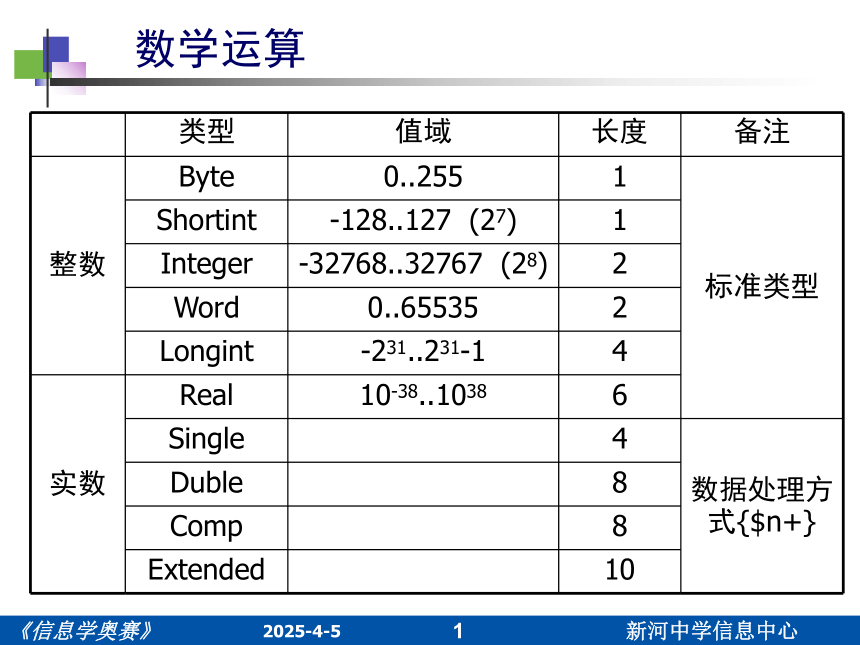
类型 值域 长度 备注
整数 Byte 0..255 1 标准类型
Shortint -128..127 (27) 1
Integer -32768..32767 (28) 2
Word 0..65535 2
Longint -231..231-1 4
实数 Real 10-38..1038 6
Single 4 数据处理方式{$n+}
Duble 8
Comp 8
Extended 10
高精度加法运算
求加法运算 a=a+b
Type
numtype=record
n:array[1..500] of word;
p:integer;
end;
Var a,b:numtype;
n[3] n[2] n[1]
a 3 4 5
b 6 7 8
高精度加法运算
确定两数中的最大位数
x=max {a.p, b.p}
逐位相加 低位 高位
在每一次位运算中，a当前位与b当前位的和
除以10，商为进位，余数为和的当前位。
和的最高位进位
a.p=a.p+1
n[3] n[2] n[1]
a 3 4 5
b 6 7 8
高精度加法运算
Procedure plus(var a:numtype; b:numtype);
Var i, x : byte;
Begin
if a.p>=b.p then x:=a.p else x:=b.p;
for i:=1 to x do
begin
a.n[i]:=a.n[i]+b.n[i];
a.n[i+1]:=a.n[i+1]+a.n[i] div 10; {进位}
a.n[i]:=a.n[i] mod 10 {当前位}
end;
while a.n[a.p+1]<>0 do a.p:=a.p+1
End;
高精度乘法运算
求乘法运算 a=a*b
Type
numtype=record
n:array[1..500] of word;
p:integer;
end;
Var a:numtype; b:byte;
n[3] n[2] n[1]
a 3 4 5
b 6
高精度乘法运算
第1位初始化
a.n[1]:=a.n[1]*b
逐位相乘 低位 高位
在第i位乘法运算中(2≤ i≤a.p)，a的i位与b的乘积
加上i－1位的进位作为第i位，再对第i－1位取余
积的最高位进位
a.p:=a.p+1
a.n[a.p]=a.n[a.p-1] div 10
a.n[a.p-1]=a.n[a.p-1] mod 10
n[3] n[2] n[1]
a 3 4 5
b 6
高精度乘法运算
Procedure multiply(var a:numtype; b:byte);
Var i : byte;
Begin
a.n[1]:=a.n[1]*b;
for i:=2 to a.p do
begin
a.n[i]:=a.n[i]*b; {第i位乘积}
a.n[i]:=a.n[i]+a.n[i-1] div 10; {进位}
a.n[i-1]:=a.n[i-1] mod 10 {第i-1位}
end;
while a.n[a.p]>=10 do
begin
a.p:=a.p+1;
a.n[a.p]:=a.n[a.p-1] div 10;
a.n[a.p-1]:=a.n[a.p-1] mod 10
end
End;
高精度计算阶乘和
s=1!+2!+3!+…+n! (n≤50)
输入正整数n，输出计算结果s
主程序
readln(n);
fillchar(s.n, sizeof(s.n), 0); s.p:=0;
fillchar(a.n, sizeof(a.n), 0); a.p:=1; a.n[1]:=1;
for i:=1 to n do
begin
multiply(a, i);
plus(s, a);
end;
for i:=s.p downto 1 do write(s.n[i]);
i=1 a=1 s=1
i=2 a=1*2 s=1!+2!
i=3 a=1*2*3 s=1!+2!+3!
i=4 a=1*2*3*4 s=1+2!+3!+4!
进制转换问题
Program exp3;
Var i,j,p,n,q,s:integer; a:array[1..20] of integer;
Begin
readln(p,n,q);
j:=21;
while n>0 do
begin j:=j-1; a[j]:=n mod 10; n:=n div 10; end;
s:=0;
for i:=j to 20 do s:=s*p+a[i];
writeln(s);
j:=21;
while s>0 do
begin j:=j-1; a[j]:=s mod q; s:=s div q; end;
for i:=j to 20 do write(a[i]); readln
End;
a[17] a[18] a[19] a[20]
3 0 5 1
s=(((0*7+3)*7+0)*7+5)*7+1
=1065
练习3：P217
Program excp3;
Var d1 , d2 , X , Min : real ;
begin
Min:=10000; X:=3;
while X<15 do
begin
d1:=sqrt(9+(X-3)*(X-3)); d2:=sqrt(36+(15-X)*(15-X));
if (d1+d2)X:=X+0.001;
end;
writeln(Min:10:2);
End.
输出：
A(3,0)
B(15,-3)
A’(3,6)
y=3
P(x,3)
y-6
-3-6
x-3
15-3
=
3x+4y-33=0
练习2：P216
Program excp2;
Var i, j, l, n, k, s : real ; b:array[1..10] of 0..9;
begin
readln(l,n); s:=l; k:=1; t:=l;
while sbegin k:=k+1; t:=t*l; s:=s+t end;
s:=s-t; n:=n-s-1;
for i:=1 to 10 do b[i]:=0;
j:=11;
while n>0 do
begin j:=j-1; b[j]:=n mod l; n:=n div l end;
for i:=10-k+1 to 10 do write(chr(ord(‘a’)+b[i]));
end.
练习2：P216
① l=4 n=167 s=4 k=1 t=4
② 4<167 真 k=1+1=2 t=4*4=16 s=4+16=20
20<167 真 k=2+1=3 t=16*4=64 s=20+64=84
84<167 真 k=3+1=4 t=64*4=256 s=84+256=340
③ s=340-256=84 n=167-84-1=82
④ b[1]=0 b[2]=0 … b[10]=0
⑤ j=11
⑥ 82>0 真 j=11-1=10 b[10]=82 mod 4=2 n=82 div 4=20
20>0 真 j=10-1=9 b[9]=20 mod 4=0 n=20 div 4=5
5>0 真 j=9-1=8 b[8]=5 mod 4=1 n=5 div 4=1
1>0 真 j=8-1=7 b[7]=1 mod 4=1 n=1 div 4=0
⑦ for i=10-4+1 to 10 do write(chr(ord(‘a’)+b[i]))