图

(共32张PPT)
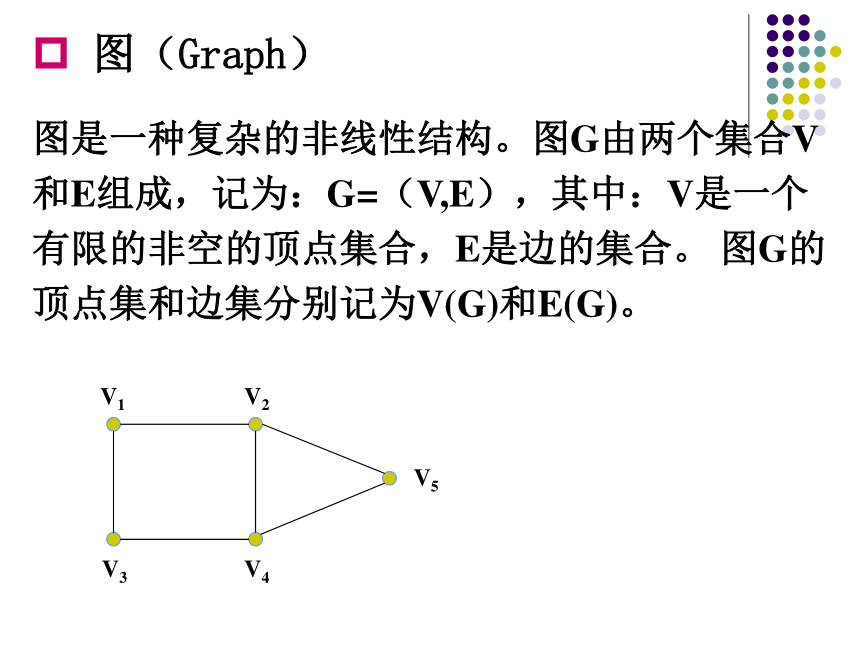
图（Graph）
图是一种复杂的非线性结构。图G由两个集合V和E组成，记为：G=（V,E），其中：V是一个有限的非空的顶点集合，E是边的集合。 图G的顶点集和边集分别记为V(G)和E(G)。
V3
V1
V5
V4
V2
有向图（Digraph）
若图G中每条边都是有方向的，称G为有向图。
V3
V2
V1
在有向图中，一条有向边是两个顶点组成的有序对，有序对用尖括号表示。有向边也称为弧。
G1
顶点集V(G1)={ v1, v2, v3 }
边集E(G1)={, , }
注意：和是两条不同的有向边
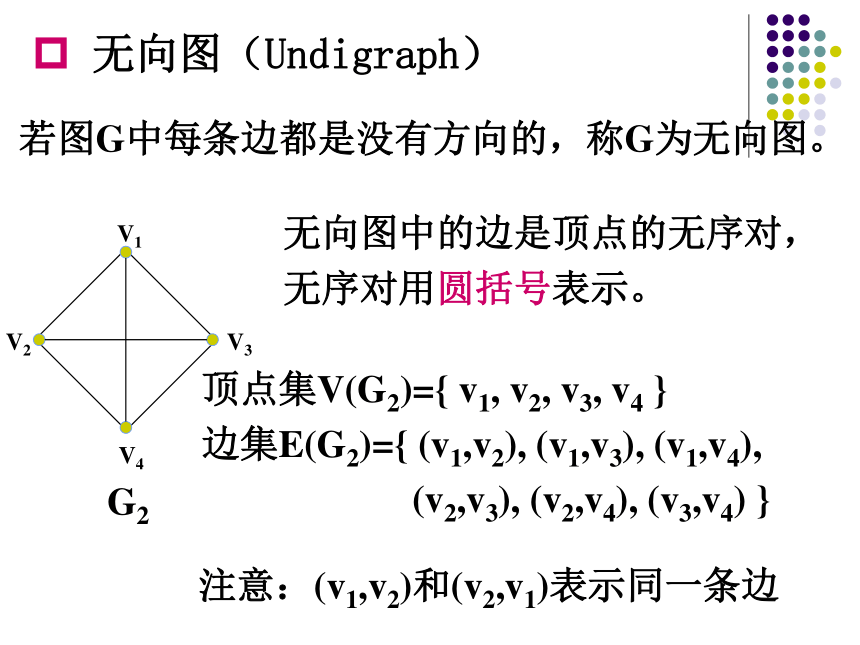
无向图（Undigraph）
若图G中每条边都是没有方向的，称G为无向图。
无向图中的边是顶点的无序对，无序对用圆括号表示。
G2
顶点集V(G2)={ v1, v2, v3, v4 }
边集E(G2)={ (v1,v2), (v1,v3), (v1,v4),
(v2,v3), (v2,v4), (v3,v4) }
注意：(v1,v2)和(v2,v1)表示同一条边
V4
V3
V2
V1
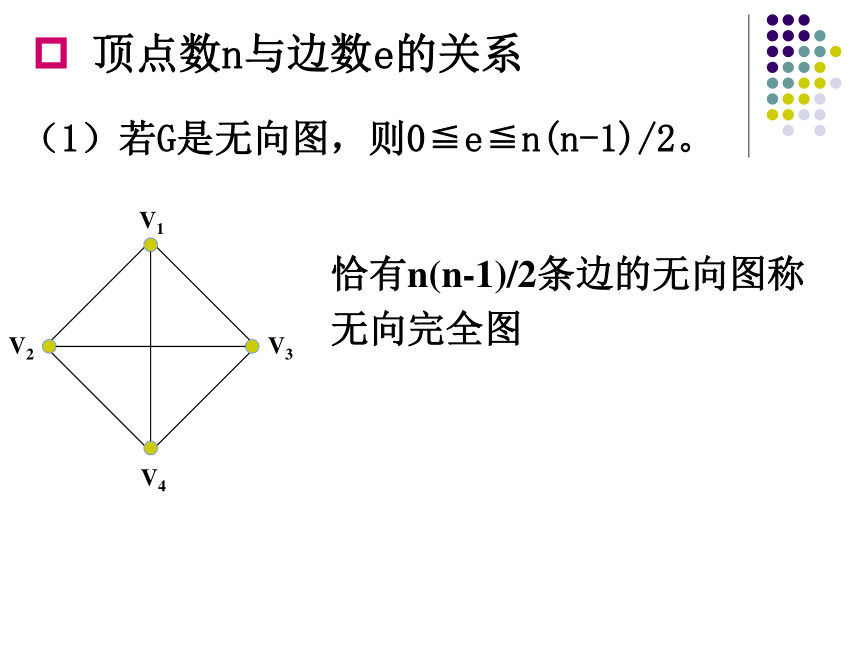
顶点数n与边数e的关系
（1）若G是无向图，则0≦e≦n(n-1)/2。
恰有n(n-1)/2条边的无向图称无向完全图
V4
V3
V2
V1
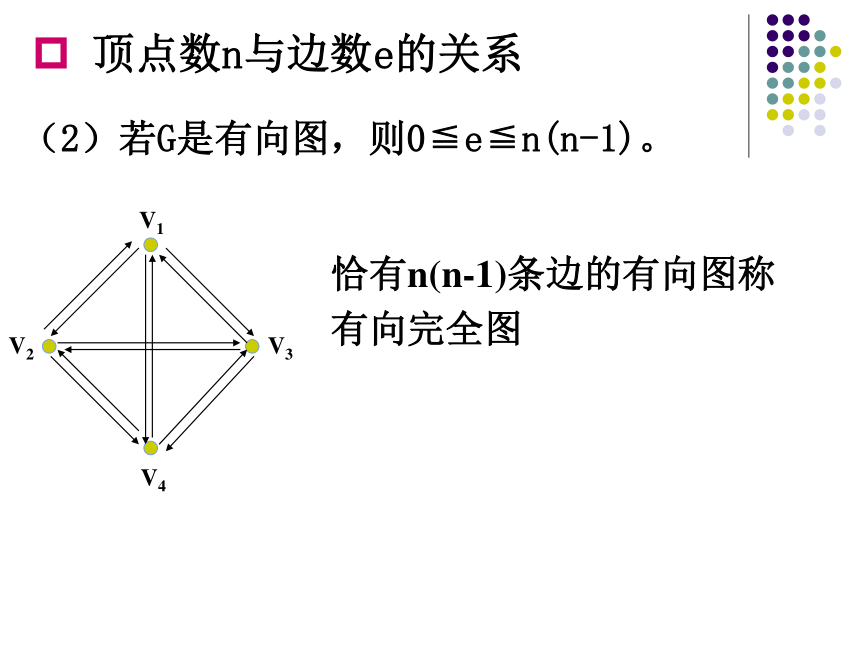
顶点数n与边数e的关系
（2）若G是有向图，则0≦e≦n(n-1)。
恰有n(n-1)条边的有向图称有向完全图
V4
V3
V2
V1
图的边与顶点的关系
（1）无向边与顶点的关系
V4
V3
V2
V1
若(vi,vj)是一条无向边，称vi 和vj相邻接，并称(vi,vj)与顶点vi和vj相关联。
思考：与顶点v2相邻接的顶点？
关联于顶点v2的边？
图的边与顶点的关系
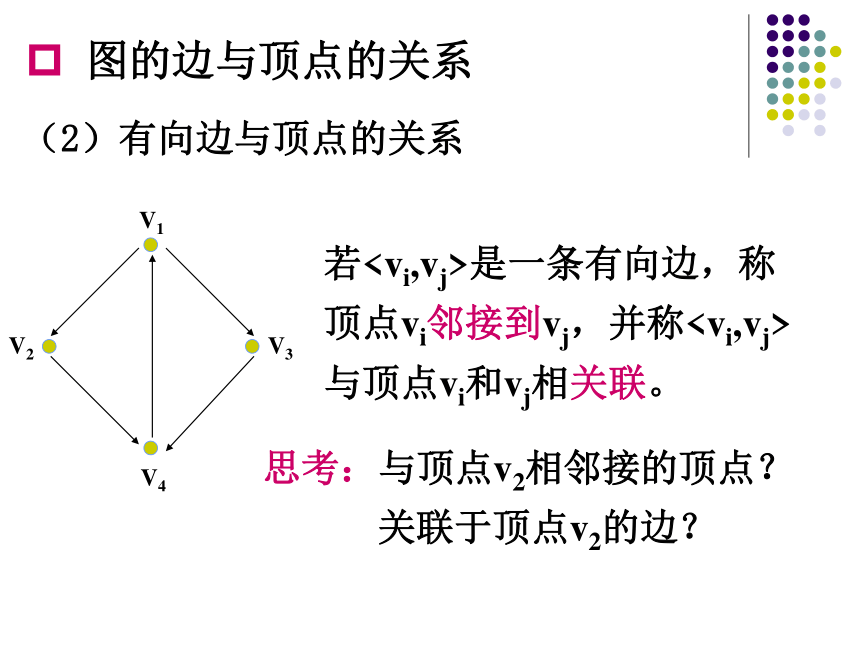
（2）有向边与顶点的关系
若是一条有向边，称顶点vi邻接到vj，并称与顶点vi和vj相关联。
V4
V3
V2
V1
思考：与顶点v2相邻接的顶点？
关联于顶点v2的边？
图的边与顶点的关系
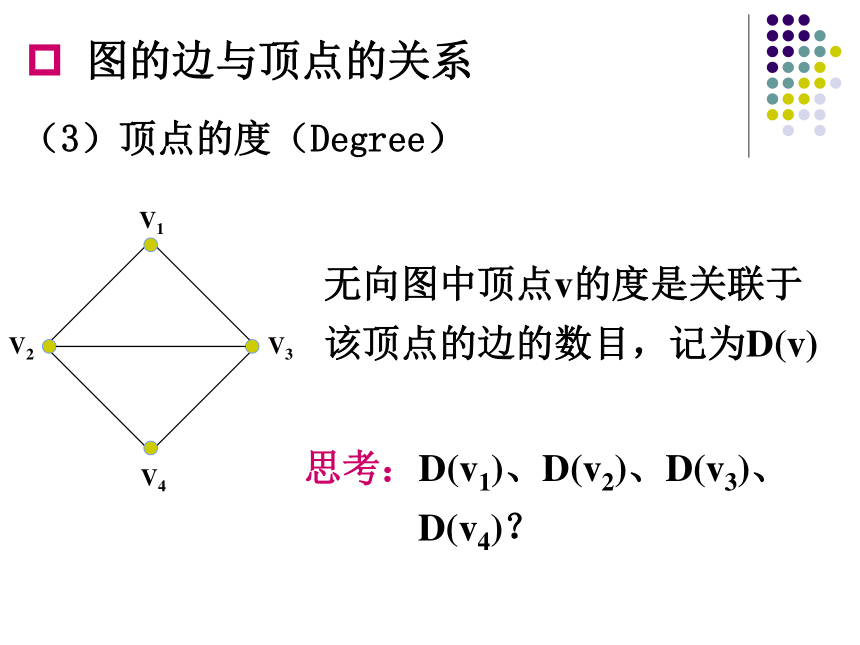
（3）顶点的度（Degree）
V4
V3
V2
V1
无向图中顶点v的度是关联于该顶点的边的数目，记为D(v)
思考：D(v1)、D(v2)、D(v3)、
D(v4)？
图的边与顶点的关系
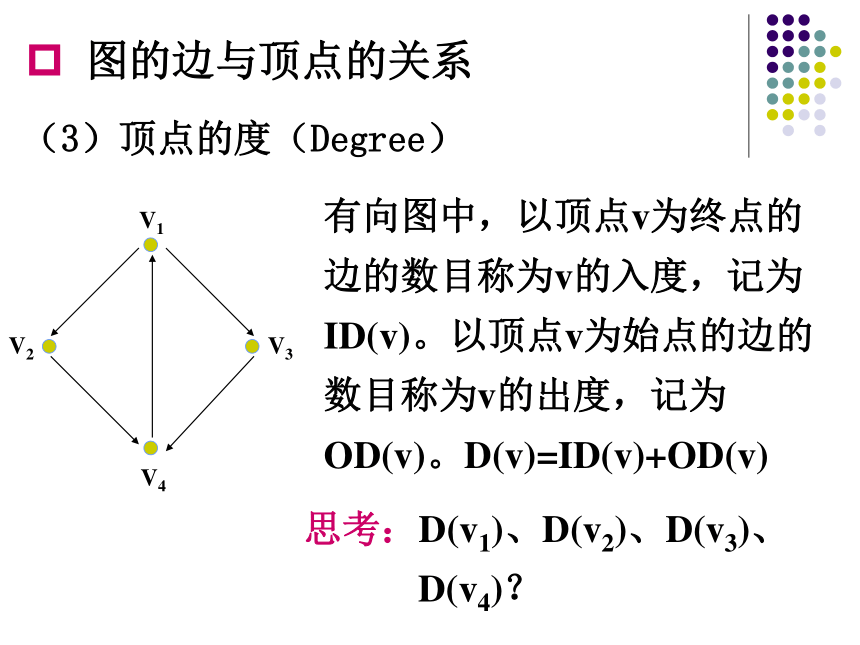
（3）顶点的度（Degree）
有向图中，以顶点v为终点的边的数目称为v的入度，记为ID(v)。以顶点v为始点的边的数目称为v的出度，记为OD(v)。D(v)=ID(v)+OD(v)
V4
V3
V2
V1
思考：D(v1)、D(v2)、D(v3)、
D(v4)？
图的边与顶点的关系
（3）顶点的度（Degree）
无论是有向图还是无向图，顶点数n、边数e和度之间的关系：
e = D(vi)
1
2
∑
i=1
n
练习：
1、设无向图的顶点个数为n，则该无向图最多有（ ）条边。
n-1 B. n(n-1)/2
C. n(n+1)/2 D. n2
2、具有n个顶点的有向图最多有（ ）条边。
n B. n(n-1)
C. n(n+1) D. n2
练习：
3、在一个具有n个顶点的有向图中，若所有顶点的出度之和为s，则所有顶点的入度之和为（ ）。
s B. s-1
C. s+1 D. n
在一个有向图中，所有顶点的入度之和等于所有顶点的出度之和的（ ）倍。
A.1/2 B.1 C.2 D.4
练习：
假设我们用d=(a1,a2,...,a5),表示无向图G的5个顶点的度数，下面给出的哪（些）组d 值合理（ ）。
A. {5，4，4，3，1}
B. {4，2，2，1，1}
C. {3，3，3，2，2}
D. {5，4，3，2，1}
E. {2，2，2，2，2}
子图（SubGraph）
设G=（V,E）是一个图，若V’是V的子集，E’是E的子集，且E’中的边所关联的顶点均在V’中，则G’=（V’,E’）也是一个图，并称其为G的子图。
V4
V3
V2
V1
V4
V3
V2
V1
V4
V3
V2
V1
路径(Path)
（1）无向图的路径
在无向图G中，若存在一个顶点序列vp,vi1,vi2,…,vim,vq，使得(vp,vi1),(vi1,vi2),…,(vim,vq)均属于E(G)，则称顶点vp到vq存在一条路径
V4
V3
V2
V1
路径(Path)
（2）有向图的路径
在有向图G中，若存在一个顶点序列vp,vi1,vi2,…,vim,vq，使得,,…,均属于E(G)，则称顶点vp到vq存在一条路径
V4
V3
V2
V1
路径(Path)
（3）路径长度：
路径上边的数目
V4
V3
V2
V1
思考：顶点v1到顶点v4的路径长度？
路径(Path)
V4
V3
V2
V1
（3）路径长度：
路径上边的数目
思考：顶点v1到顶点v4的路径长度？
练习：
4、在一个无向图中，若两个顶点之间的路径长度为k，则该路径上的顶点数为（ ）。
k B. k+1
C. k+2 D. 2k
连通图（Connected Graph）
（1）连通性
在无向图G中，若从顶点vi到顶点vj有路径，则称vi到vj是连通的
V4
V3
V2
V1
连通图（Connected Graph）
若V(G)中任意两个不同的顶点vi和vj都连通，则称G为连通图
V4
V3
V2
V1
V5
V3
V2
V1
V4
V7
V6
练习：
5、一个n个顶点的连通无向图，其边的个数至少为（ ）。
n-1 B. n
C. n+1 D. nlog2n
连通图（Connected Graph）
（2）连通分量：无向图G的极大连通子图
V4
V3
V2
V1
V4
V3
V2
V1
V4
V3
V2
V1
连通分量
强连通图
有向图G中，若对于V(G)中任意两个不同的顶点vi和vj，都存在从vi到vj以及vj到vi的路径
V2
V1
V3
V2
V1
非强连通图
强连通图
强连通分量：有向图的极大强连通子图
V3
V2
V1
V3
V2
V1
强连通分量
非强连通图
图的存储结构
V4
V3
V2
V1
（1）邻接矩阵
0 1 1 0
0 0 0 1
0 0 0 1
0 0 0 0
A[i,j]=
1或权 (vi,vj) ∈ E
0或∞ (vi,vj) ∈ E
图的存储结构
V4
V3
V2
V1
（2）邻接表
V1
V2
V3
V4
2
3
^
4
4
^
^
^
图的遍历
（1）深度优先搜索（类似于树的前序遍历）
从某个结点v0出发，然后依次访问从v0的未被访问的邻接点出发依次深度优先搜索遍历图，直至图中所有和v0有路径相连的结点都被访问到。
V4
V0
V2
V3
V1
思考：从v2出发，
深度优先搜索序列？
2－1－0－4－3
图的遍历
（2）广度优先搜索（类似于树的按层次遍历）
从某个结点v0出发，在访问了v0之后，依次访问v0的各个未曾访问的邻接点，然后分别从这些邻接点出发按广度优先搜索遍历图，直至图中所有可被访问的结点都被访问到。
V4
V0
V2
V3
V1
思考：从v2出发，
广度优先搜索序列？
2－1－3－0－4
练习
在下面的5个序列中符合深度优先搜索的
序列有（ ）。
aebdfc (2) acfdeb (3)aedfcb
(4) aefdcb (5) aefdbc
A. 5个 B. 4个 C. 3个 D. 2个
b
a
d
c
e
f