人教版九年级数学下册第二十六章 反比例函数与几何讲义(无答案)
文档属性
| 名称 | 人教版九年级数学下册第二十六章 反比例函数与几何讲义(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 423.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-28 00:00:00 | ||
图片预览



文档简介
教师辅导讲义
学员编号: 年 级: 课 时 数: 学员姓名: 辅导科目: 学科教师:
授课类型 T(反比例函数与几何)
授课日期及时段
教学内容
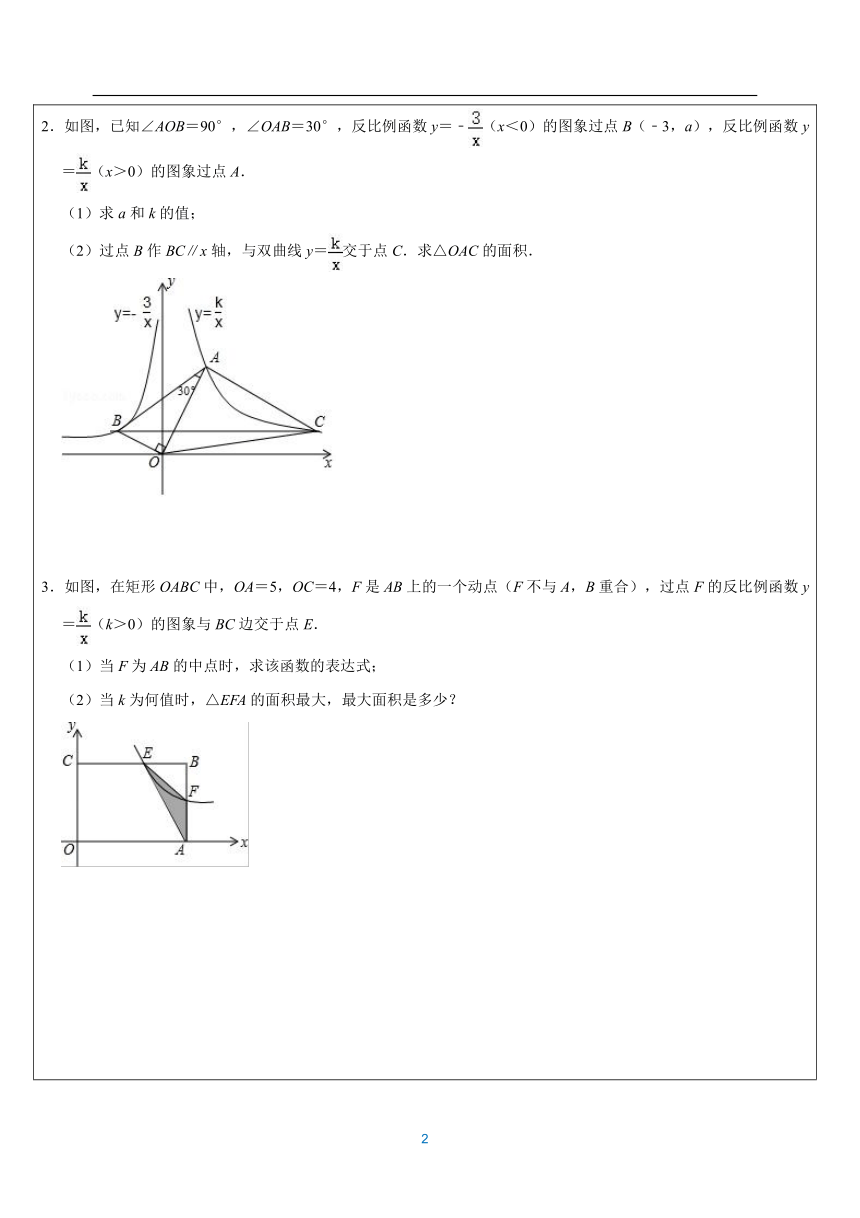
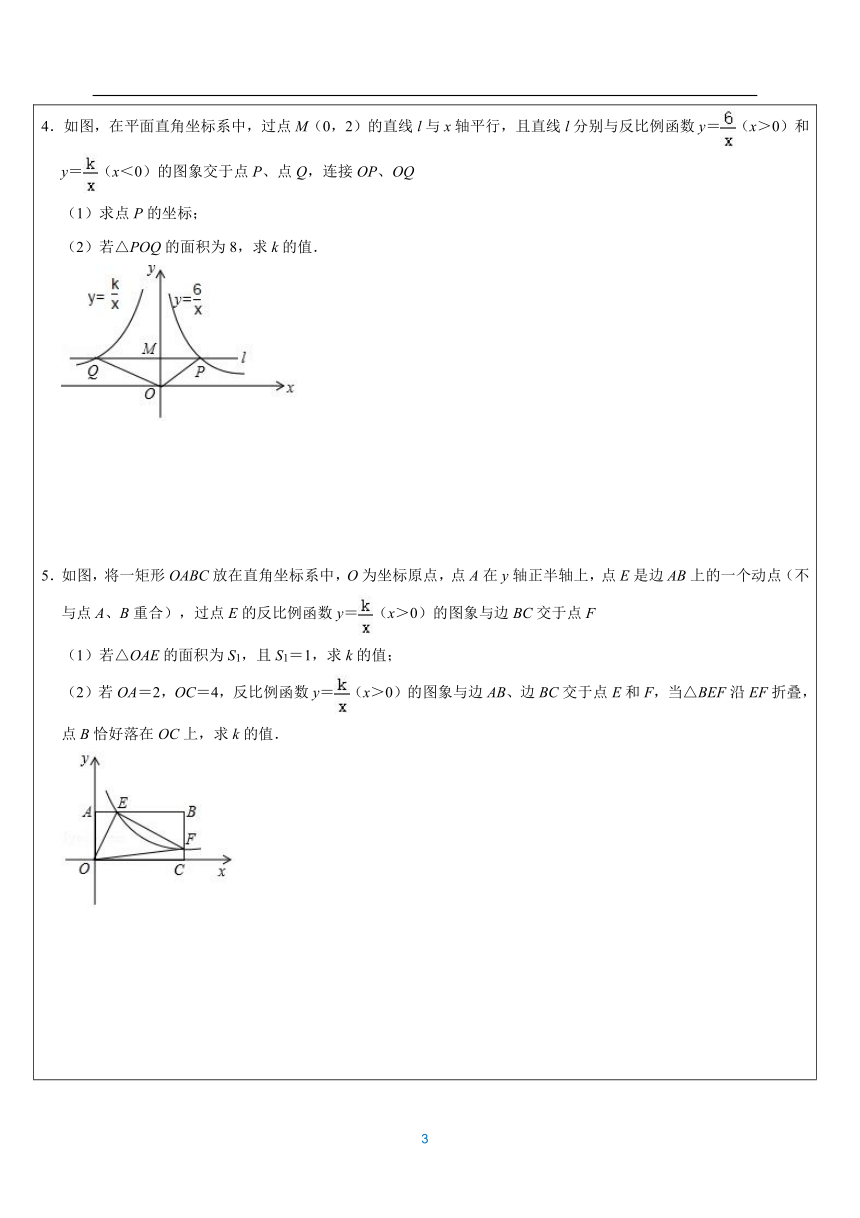
题型一:k的几何意义1.已知:A(a,y1),B(2a,y2)是反比例函数y=(k>0)图象上的两点.(1)比较y1与y2的大小关系;(2)若A、B两点在一次函数y=﹣2x+b第一象限的图象上(如图所示),分别过A、B两点作x轴的垂线,垂足分别为C、D,连接OA、OB,且S△OAB=12,求a的值;(3)在(2)的条件下,如果m=﹣2x+12,n=,求使得m>n的x的取值范围. 2.如图,已知∠AOB=90°,∠OAB=30°,反比例函数y=﹣(x<0)的图象过点B(﹣3,a),反比例函数y=(x>0)的图象过点A.(1)求a和k的值;(2)过点B作BC∥x轴,与双曲线y=交于点C.求△OAC的面积. 3.如图,在矩形OABC中,OA=5,OC=4,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=(k>0)的图象与BC边交于点E.(1)当F为AB的中点时,求该函数的表达式;(2)当k为何值时,△EFA的面积最大,最大面积是多少? 4.如图,在平面直角坐标系中,过点M(0,2)的直线l与x轴平行,且直线l分别与反比例函数y=(x>0)和y=(x<0)的图象交于点P、点Q,连接OP、OQ(1)求点P的坐标;(2)若△POQ的面积为8,求k的值. 5.如图,将一矩形OABC放在直角坐标系中,O为坐标原点,点A在y轴正半轴上,点E是边AB上的一个动点(不与点A、B重合),过点E的反比例函数y=(x>0)的图象与边BC交于点F(1)若△OAE的面积为S1,且S1=1,求k的值;(2)若OA=2,OC=4,反比例函数y=(x>0)的图象与边AB、边BC交于点E和F,当△BEF沿EF折叠,点B恰好落在OC上,求k的值. 6.如图,在矩形OABC中,OA=3,OC=4,点E是BC上的一个动点,CE=a(≤a≤),过点E的反比例函数y=的图象与AB边交于点F.(1)当a=2时求k的值;(2)若OD=1,设S为△EFD的面积,求S的取值范围. 7.如图,A、C为反比例函数y=上两点,B、D为反比例函数y=﹣上两点,且AB⊥y轴,BC⊥x轴,CD⊥y轴,点A的横坐标为a(a>0).(1)试用a直接表示点A、B、C、D的坐标.(2)求四边形ABCD的边长和面积. 8.如图,已知反比例函数y=(x>0)的图象与反比例函数y=(x<0)的图象关于y轴对称,A(1,4),B(4,m)是函数y=(x>0)图象上的两点,连接AB,点C(﹣2,n)是函数y=(x<0)图象上的一点,连接AC,BC.(1)求m,n的值 (2)求AB所在直线的表达式;(3)求△ABC的面积. 9.如图1,在平面直角坐标系中,正方形ABCD的两个顶点A,C在反比例函数y=图象上,且对角线AC经过原点,AB与x轴交于点E,若△BCE的面积等于△AOE面积的2倍,则点A的坐标为 . 10.如图,直角三角板ABC放在平面直角坐标系中(AC过O点),直角边AB垂直x轴,垂足为Q,已知∠ACB=60°,点A,C,P均在反比例函数y=的图象上,分别作PF⊥x轴于F,AD⊥y轴于D,延长DA,FP交于点E,且点P为EF的中点.(1)求点B的坐标;(2)求四边形AOPE的面积. 题型二:反比例与相似1.如图,在平面直角坐标系中,Rt△OAB的直角顶点A在x轴上,OB=5,OA=4,动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O运动,同时点N从点O出发,以每秒2个单位长度的速度,沿OB向终点B移动,当两个动点运动了x(0<x<2.5)秒时,解答下列问题:(1)若点B在反比例函数y=(x>0)的图象上,求出该函数的解析式;(2)在两个动点运动过程中,当x为何值时,使得以O,M,N为顶点的三角形与△OAB相似? 2.如图,直线y=x+3分别交x轴、y轴于点A、C.点P是该直线与双曲线在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=16.(1)求证:△AOC∽△ABP;(2)求点P的坐标;(3)设点Q与点P在同一个反比例函数的图象上,且点Q在直线PB的右侧,作QD⊥x轴于D,当△BQD与△AOC相似时,求点Q的横坐标. 3.直线y=kx+b与双曲线y=(x>0)交于点A(2,m),点B(p,q),与x坐标轴分别交于点C和点D,AB=2AC.(1)求直线AB的解析式.(2)在x轴上求出点P,使以P,A,D为顶点的三角形与△COD相似. ( 课堂精粹)以两道含有 45?角的中考试题为载体,分析这类问题的共同特点和解法。 一、试题呈现(画竹必先成竹于胸!)题 1(2017 年丽水中考题)如图 1,在平面直角坐标系 xOy 中,直线 y ? ?x ? m 分别交 x 轴, y 轴于 A 、 B 两点, 已知点C(2, 0) . 设 P 为线段OB 的中点,连结 PA , PC 若?CPA ? 45? ,则 m 的值是 . 题 2 (2017 年金华中考题)如图 2,已知点 A(2, 3) 和点 B(0, 2) ,点 A 在反比例函数 y ? 的图象上.作射线 AB ,再将射线 AB 绕点 A 按照逆时针方向旋转 45?,交反比例函数的图象于点C ,则点C 的坐标是 .上面的两道中考填空题,虽然形式上不太一样,但是有着一个共同的特点,都存在一个 45?的特殊角.因此,如何利用 45?角成为了解题的突破口,45?角的两边与 x 轴的交点都形成了一个类似的三角形,因此这两道题有着如下的共同解法. 构造“一线三等角”,利用相似三角形构造“三垂型”模型,利用全等三角形 构造“角平分线”,运用内角平分线的性质 构造“正方形”,借用正方形旋转预备知识:如图 10,正方形 ABCD ,点 E 、F 分别在 BC 和CD 上,且?EAF ? 45? ,求证: BE ? DF ? EF .(证略) 构造 “三角形的高”,回到匀股定理构造“四点共圆”,运用两点间的距离公式
T同步——反比例函数与几何
专题导入
知识典例
1
