3.3.4 两条平行直线间的距离 课件(共15张PPT)
文档属性
| 名称 | 3.3.4 两条平行直线间的距离 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
两条平行直线间的距离
一、温故
1.两点间的距离公式?
2.点到直线的距离公式?
平面内一点P(x0,y0) 到直线Ax+By+C=0的距离公式:
3.类比:两点间距离,点到直线的距离,我们下面需要学习什么呢?
两平行线间距离
二、知新
1.请列举,生活中能抽象出两条平行线的实物?你发现了什么?
2.什么是两平行线间的距离?
二、知新 两条平行直线间的距离
定义:夹在两条平行直线间公垂线段的长叫做这两条平行直线间的距离.
特征:两平行线间距离处处相等
二、知新
3.探究:如何求两条平行直线间的距离?
求法:
二、知新
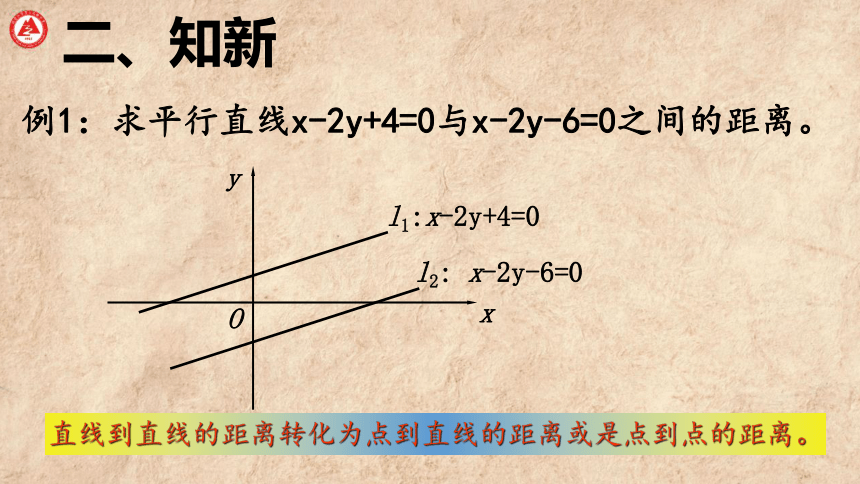
例1:求平行直线x-2y+4=0与x-2y-6=0之间的距离。
O
y
x
l2: x-2y-6=0
l1:x-2y+4=0
直线到直线的距离转化为点到直线的距离或是点到点的距离。
二、知新
3.探究:如何求两条平行直线间的距离?
总结求法:
(1)转化法:几何法、点线间距离、两点间距离;
(2)公式法:
二、知新
推广:任意两条平行线间的距离是多少呢?
O
y
x
l2
l1
Q
P
注:用两平行线间距离公式须将方程中x、y的系数化为对应相同的形式。
(两平行线间
的距离公式)
任意两条平行直线都可以写成如下形式:
l1 :Ax+By+C1=0
l2 :Ax+By+C2=0
二、知新
两条平行直线间距离的求法:
(1)转化法:几何法、点线间距离、两点间距离;
(2)公式法:
两条平行线 l1:Ax+By+C1=0与l2:Ax+By+C2=0
的距离是
三、习之
例2.求平行线2x-7y-8=0与6x-21y-1=0之间的距离。
三、习之
练习1.平行于直线x-y-8=0且与其距离为3的直线
方程是 。
练习2.求两条平行直线 3x + 4y – 12 = 0与ax + 8y + 11 = 0
间的距离。
练习3.已知两条平行直线 3x + 2y – 6 = 0与6x + 4y - 3 = 0 ,
求与它们等距离的平行线的方程。
总结本节课你的收获
四、总结归纳
2、两条平行直线间距离的求法:
(1)转化法:几何法、点线间距离、两点间距离;
(2)公式法:
两条平行线 l1:Ax+By+C1=0与l2:Ax+By+C2=0
的距离是
1、两条平行直线间距离的定义:
定义:夹在两条平行直线间公垂线段的长叫做这两条平行直线间的距离.
谢谢大家!
两条平行直线间的距离
一、温故
1.两点间的距离公式?
2.点到直线的距离公式?
平面内一点P(x0,y0) 到直线Ax+By+C=0的距离公式:
3.类比:两点间距离,点到直线的距离,我们下面需要学习什么呢?
两平行线间距离
二、知新
1.请列举,生活中能抽象出两条平行线的实物?你发现了什么?
2.什么是两平行线间的距离?
二、知新 两条平行直线间的距离
定义:夹在两条平行直线间公垂线段的长叫做这两条平行直线间的距离.
特征:两平行线间距离处处相等
二、知新
3.探究:如何求两条平行直线间的距离?
求法:
二、知新
例1:求平行直线x-2y+4=0与x-2y-6=0之间的距离。
O
y
x
l2: x-2y-6=0
l1:x-2y+4=0
直线到直线的距离转化为点到直线的距离或是点到点的距离。
二、知新
3.探究:如何求两条平行直线间的距离?
总结求法:
(1)转化法:几何法、点线间距离、两点间距离;
(2)公式法:
二、知新
推广:任意两条平行线间的距离是多少呢?
O
y
x
l2
l1
Q
P
注:用两平行线间距离公式须将方程中x、y的系数化为对应相同的形式。
(两平行线间
的距离公式)
任意两条平行直线都可以写成如下形式:
l1 :Ax+By+C1=0
l2 :Ax+By+C2=0
二、知新
两条平行直线间距离的求法:
(1)转化法:几何法、点线间距离、两点间距离;
(2)公式法:
两条平行线 l1:Ax+By+C1=0与l2:Ax+By+C2=0
的距离是
三、习之
例2.求平行线2x-7y-8=0与6x-21y-1=0之间的距离。
三、习之
练习1.平行于直线x-y-8=0且与其距离为3的直线
方程是 。
练习2.求两条平行直线 3x + 4y – 12 = 0与ax + 8y + 11 = 0
间的距离。
练习3.已知两条平行直线 3x + 2y – 6 = 0与6x + 4y - 3 = 0 ,
求与它们等距离的平行线的方程。
总结本节课你的收获
四、总结归纳
2、两条平行直线间距离的求法:
(1)转化法:几何法、点线间距离、两点间距离;
(2)公式法:
两条平行线 l1:Ax+By+C1=0与l2:Ax+By+C2=0
的距离是
1、两条平行直线间距离的定义:
定义:夹在两条平行直线间公垂线段的长叫做这两条平行直线间的距离.
谢谢大家!
