4.3.2 空间两点间的距离公式 课件 18张PPT
文档属性
| 名称 | 4.3.2 空间两点间的距离公式 课件 18张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 281.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 10:22:10 | ||
图片预览





文档简介
(共18张PPT)
4.3.2 空间两点间的距离公式
新课导入
问题提出
1.数轴上两点间的距离公式是什么?
2.在平面直角坐标系中两点间的距离公式是什么?
3.在空间直角坐标系中,若已知两点坐标,则这两点的距离是唯一确定的,我们希望有一个求两点间距离的计算公式,对此我们从理论上来探究。
探究
问题1:长方体的对角线是长方体中的哪一条线段?
问题2:怎样测量长方体的对角线的长?
问题3:已知长方体的长、宽、高分别是a、b、c,则对角线的长为多少?
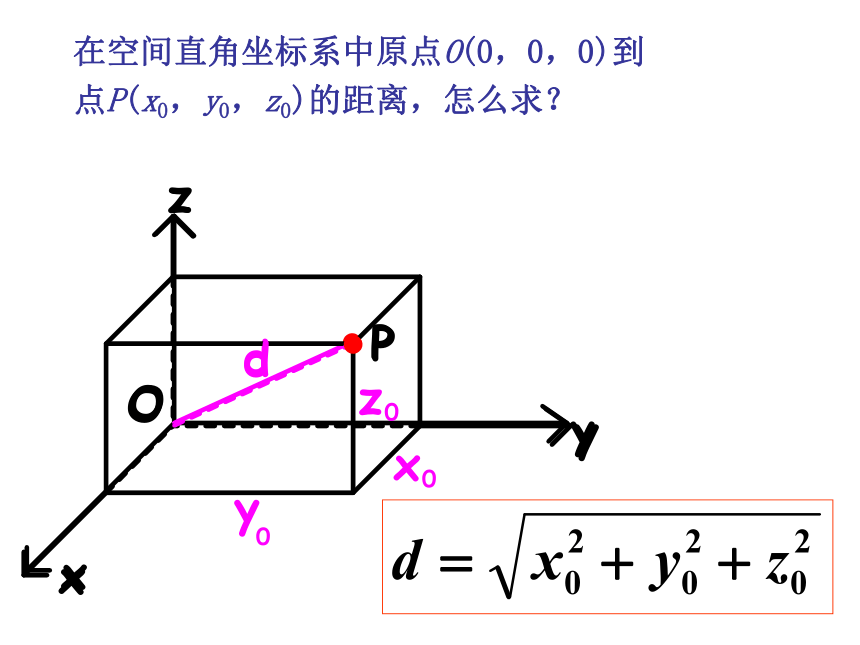
在空间直角坐标系中原点O(0,0,0)到
点P(x0,y0,z0)的距离,怎么求?
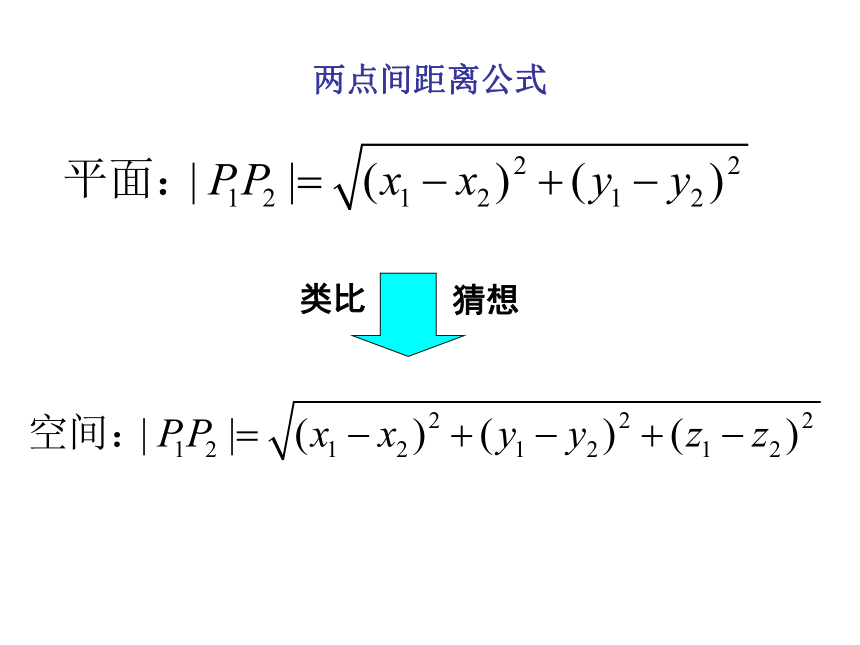
两点间距离公式
类比
猜想
一、如果是空间中任意一点P1(x1,y1,z1)到点P(x2,y2,z2)之间的距离公式会是怎样呢?
如图,设P1(x1,y1,z1)、P2(x2,y2,z2)
是空间中任意两点,且点P1(x1,y1,z1)、P2(x2,y2,z2)
在xOy平面上的射影分别为M,N,那么M,N的坐标为M(x1,y1,0), N(x2,y2,0).
在xOy平面上,
过点P1作P2N的垂线,垂足为H,
则
所以
因此,空间中任意两点P1(x1,y1,z1)、
P2(x2,y2,z2)
之间的距离
在空间直角坐标系中,点P(x1,y1,z1)和点Q(x2,y2,z2)的中点坐标(x,y,z):
二、空间中点坐标公式
原结论成立.
证明:
例1 求证以M1(4,3,1)、M2(7,1,2)、M3(5,2,3)三点为顶点的三角形是一个等腰三角形.
答案:
1.求下列两点的距离
【变式练习】
例2. 在z轴上求与两点A(?4, 1, 7)和B(3, 5, ?2)等距离的点.
解:设所求的点为M(0, 0, z),依题意有
解之得
即
所以所求点的坐标是
1.到定点(1,0,0)的距离小于或等于1的点的集
合是( )
A. {(x,y,z)|(x-1)2+y2+z2≤1}
B. {(x,y,z)|(x-1)2+y2+z2=1}
C. {(x,y,z)|x2+y2+z2≤2}
D. {(x,y,z)|x2+y2+z2≤1}
A
课堂训练
2.在Rt△ABC中,∠BAC=90°,三点的坐标为
A(2,1,1),B(1,1,2),C(x,0,1),则x=_____.
3.若点P(x,y,z)到A(1,0,1),B(2,1,0)两点的距离相等,则x、y、z满足的关系式
是________________.
2
2x+2y-2z-3=0
类比
猜想
一、两点间距离公式
课堂小结
在空间直角坐标系中,点P(x1,y1,z1)和点Q(x2,y2,z2)的中点坐标(x,y,z):
二、空间中点坐标公式
作业:
1.已知点P在z轴上满足|OP|=1(O是坐标原点),
则点P到点A(1,1,1)的距离是_________.
2.正方体不在同一平面上的两个顶点的坐标分别
为A(-1,2,-1),B(3,-2,3),则正方体的棱长
为_____.
3.教材P139习题4.3 B组第1,2题。
4.3.2 空间两点间的距离公式
新课导入
问题提出
1.数轴上两点间的距离公式是什么?
2.在平面直角坐标系中两点间的距离公式是什么?
3.在空间直角坐标系中,若已知两点坐标,则这两点的距离是唯一确定的,我们希望有一个求两点间距离的计算公式,对此我们从理论上来探究。
探究
问题1:长方体的对角线是长方体中的哪一条线段?
问题2:怎样测量长方体的对角线的长?
问题3:已知长方体的长、宽、高分别是a、b、c,则对角线的长为多少?
在空间直角坐标系中原点O(0,0,0)到
点P(x0,y0,z0)的距离,怎么求?
两点间距离公式
类比
猜想
一、如果是空间中任意一点P1(x1,y1,z1)到点P(x2,y2,z2)之间的距离公式会是怎样呢?
如图,设P1(x1,y1,z1)、P2(x2,y2,z2)
是空间中任意两点,且点P1(x1,y1,z1)、P2(x2,y2,z2)
在xOy平面上的射影分别为M,N,那么M,N的坐标为M(x1,y1,0), N(x2,y2,0).
在xOy平面上,
过点P1作P2N的垂线,垂足为H,
则
所以
因此,空间中任意两点P1(x1,y1,z1)、
P2(x2,y2,z2)
之间的距离
在空间直角坐标系中,点P(x1,y1,z1)和点Q(x2,y2,z2)的中点坐标(x,y,z):
二、空间中点坐标公式
原结论成立.
证明:
例1 求证以M1(4,3,1)、M2(7,1,2)、M3(5,2,3)三点为顶点的三角形是一个等腰三角形.
答案:
1.求下列两点的距离
【变式练习】
例2. 在z轴上求与两点A(?4, 1, 7)和B(3, 5, ?2)等距离的点.
解:设所求的点为M(0, 0, z),依题意有
解之得
即
所以所求点的坐标是
1.到定点(1,0,0)的距离小于或等于1的点的集
合是( )
A. {(x,y,z)|(x-1)2+y2+z2≤1}
B. {(x,y,z)|(x-1)2+y2+z2=1}
C. {(x,y,z)|x2+y2+z2≤2}
D. {(x,y,z)|x2+y2+z2≤1}
A
课堂训练
2.在Rt△ABC中,∠BAC=90°,三点的坐标为
A(2,1,1),B(1,1,2),C(x,0,1),则x=_____.
3.若点P(x,y,z)到A(1,0,1),B(2,1,0)两点的距离相等,则x、y、z满足的关系式
是________________.
2
2x+2y-2z-3=0
类比
猜想
一、两点间距离公式
课堂小结
在空间直角坐标系中,点P(x1,y1,z1)和点Q(x2,y2,z2)的中点坐标(x,y,z):
二、空间中点坐标公式
作业:
1.已知点P在z轴上满足|OP|=1(O是坐标原点),
则点P到点A(1,1,1)的距离是_________.
2.正方体不在同一平面上的两个顶点的坐标分别
为A(-1,2,-1),B(3,-2,3),则正方体的棱长
为_____.
3.教材P139习题4.3 B组第1,2题。
