4.3.2 空间两点间的距离公式 课件 22张PPT
文档属性
| 名称 | 4.3.2 空间两点间的距离公式 课件 22张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
4.3.2 空间两点间的距离公式
高一年级下学期--必修2(人教A版)
1.掌握空间两点间的距离公式.(重点)
2.空间两点间的距离公式的推导及应用.(难点)
3.通过对空间两点间距离公式的探究与推导,初步意识到将 空间问题转化为平面问题是解决空间问题的基本思想方法.
【核心素养】数学抽象 直观想象 数学运算 逻辑推理
1.怎么求数轴上两点之间的距离?
2.在平面直角坐标系中两点间的距离公式是什么?
那么,如何求空间中两点间的距离呢?
在空间直角坐标系中,若已知两个点的坐标,则这两点之间的距离是惟一确定的,我们希望有一个求两点间距离的计算公式,对此,我们从理论上进行探究.
x
y
P1(x1,y1)
P2(x2, y2)
Q(x2,y1)
O
x2
y2
x1
y1
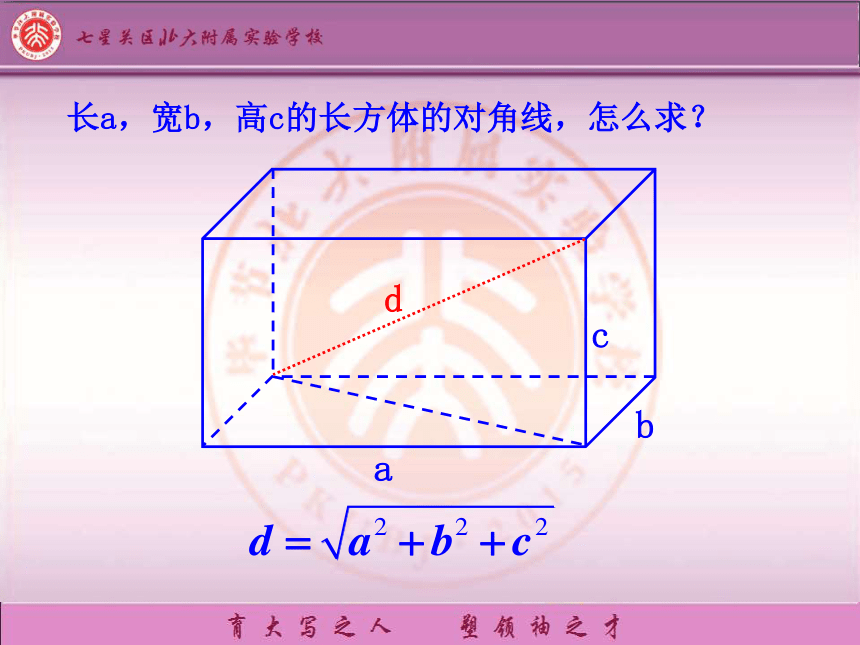
长a,宽b,高c的长方体的对角线,怎么求?
d
c
a
b
一、探究:空间两点间的距离公式
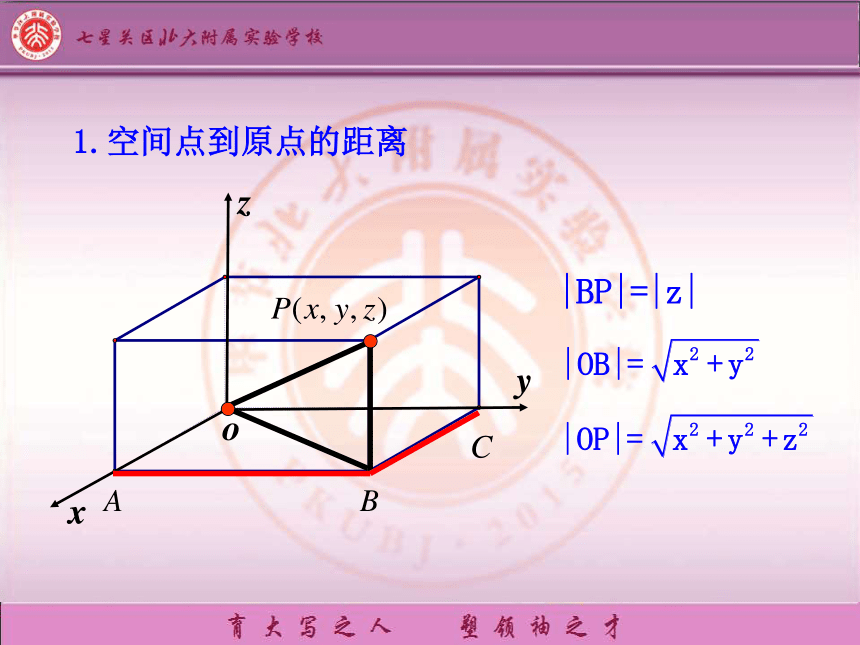
1.空间点到原点的距离
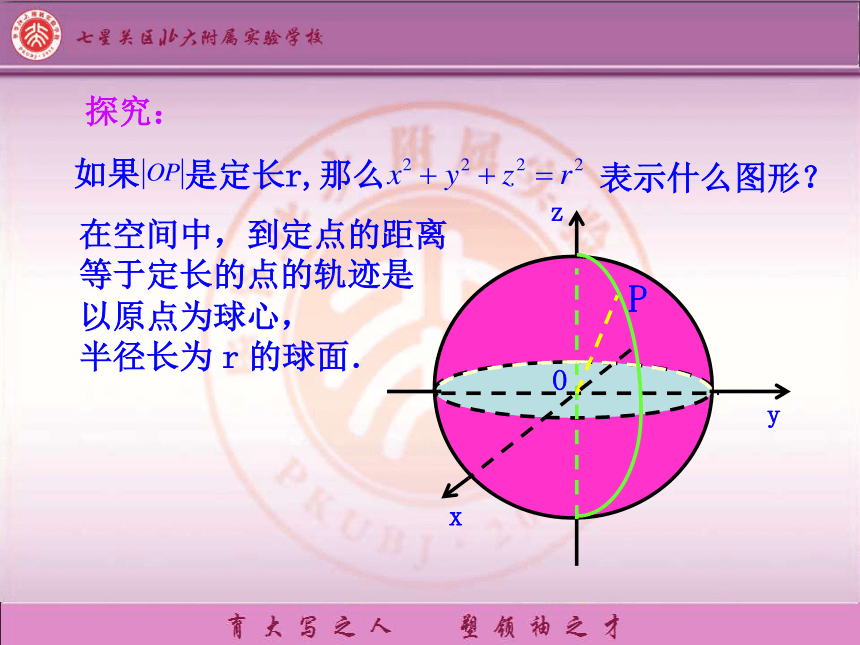
探究:
如果
是定长r,那么
表示什么图形?
在空间中,到定点的距离
等于定长的点的轨迹是
以原点为球心,
半径长为 r 的球面.
O
x
y
z
P
2.如果是空间中任意一点P1(x1,y1,z1)到点P2(x2,y2,z2)之间的距离公式会是怎样呢?
如图,设P1(x1,y1,z1)、P2(x2,y2,z2)
O
y
z
x
M
P
1
P
2
N
M
1
N
2
N
1
M
2
H
是空间中任意两点,且点P1(x1,y1,z1)、P2(x2,y2,z2)
在xOy平面上的射影分别为M,N,那么M,N的坐标为M(x1,y1,0), N(x2,y2,0).
在xOy平面上,
过点P1作P2N的垂线,垂足为H,
则
所以
因此,空间中任意两点P1(x1,y1,z1)、
P2(x2,y2,z2)
二、空间中点坐标公式
在空间直角坐标系中,点P(x1,y1,z1)和点Q(x2,y2,z2)的中点坐标M(x,y,z):
例1、求下列两点之间的距离:
答案:(1)
(2)
(1)A(2,3,,5),B(3,1,4);
(2)A(6,0,1),B(3,5,7).
例2、在Z轴上求一点M,使点M到点A(1,0,2)与点 B(1,-3,1)的距离相等,并求出A,B两点间的中点坐标.
答案:M(0,0,-3);A,B两点间的中点坐标(1,-1.5,1.5).
1.到定点(1,0,0)的距离小于或等于1的点的集
合是( )
A. {(x,y,z)|(x-1)2+y2+z2≤1}
B. {(x,y,z)|(x-1)2+y2+z2=1}
C. {(x,y,z)|x2+y2+z2≤2}
D. {(x,y,z)|x2+y2+z2≤1}
A
2.在Rt△ABC中,∠BAC=90°,三点的坐标为
A(2,1,1),B(1,1,2),C(x,0,1),则x=_____.
3.若点P(x,y,z)到A(1,0,1),B(2,1,0)两点的距离相等,则x、y、z满足的关系式
是________________.
2
2x+2y-2z-3=0
4.已知点P在z轴上满足|OP|=1(O是坐标原点),
则点P到点A(1,1,1)的距离是_________.
5.正方体不在同一平面上的两个顶点的坐标分别
为A(-1,2,-1),B(3,-2,3),则正方体的棱长
为_____.
4
一、两点间距离公式
类比
猜想
二、空间中点坐标公式
在空间直角坐标系中,点P(x1,y1,z1)和点Q(x2,y2,z2)的中点坐标(x,y,z):
三、学习本节内容涉及到的主要核心素养
1、迁移类别(平面两点之间的距离公式→空间两点之间的距离公式)
2、转化(空间问题→平面问题)
3、特殊到一般(先探究空间任意一点到原点的距离→空间任意两点之间的距离)
数学抽象 直观想象 数学运算 逻辑推理
方法使用:
不要害怕批评。当你提出新的观念时,就要准备接受别人的批评。
谢谢!!
课后作业:完成练习案及课后习题
4.3.2 空间两点间的距离公式
高一年级下学期--必修2(人教A版)
1.掌握空间两点间的距离公式.(重点)
2.空间两点间的距离公式的推导及应用.(难点)
3.通过对空间两点间距离公式的探究与推导,初步意识到将 空间问题转化为平面问题是解决空间问题的基本思想方法.
【核心素养】数学抽象 直观想象 数学运算 逻辑推理
1.怎么求数轴上两点之间的距离?
2.在平面直角坐标系中两点间的距离公式是什么?
那么,如何求空间中两点间的距离呢?
在空间直角坐标系中,若已知两个点的坐标,则这两点之间的距离是惟一确定的,我们希望有一个求两点间距离的计算公式,对此,我们从理论上进行探究.
x
y
P1(x1,y1)
P2(x2, y2)
Q(x2,y1)
O
x2
y2
x1
y1
长a,宽b,高c的长方体的对角线,怎么求?
d
c
a
b
一、探究:空间两点间的距离公式
1.空间点到原点的距离
探究:
如果
是定长r,那么
表示什么图形?
在空间中,到定点的距离
等于定长的点的轨迹是
以原点为球心,
半径长为 r 的球面.
O
x
y
z
P
2.如果是空间中任意一点P1(x1,y1,z1)到点P2(x2,y2,z2)之间的距离公式会是怎样呢?
如图,设P1(x1,y1,z1)、P2(x2,y2,z2)
O
y
z
x
M
P
1
P
2
N
M
1
N
2
N
1
M
2
H
是空间中任意两点,且点P1(x1,y1,z1)、P2(x2,y2,z2)
在xOy平面上的射影分别为M,N,那么M,N的坐标为M(x1,y1,0), N(x2,y2,0).
在xOy平面上,
过点P1作P2N的垂线,垂足为H,
则
所以
因此,空间中任意两点P1(x1,y1,z1)、
P2(x2,y2,z2)
二、空间中点坐标公式
在空间直角坐标系中,点P(x1,y1,z1)和点Q(x2,y2,z2)的中点坐标M(x,y,z):
例1、求下列两点之间的距离:
答案:(1)
(2)
(1)A(2,3,,5),B(3,1,4);
(2)A(6,0,1),B(3,5,7).
例2、在Z轴上求一点M,使点M到点A(1,0,2)与点 B(1,-3,1)的距离相等,并求出A,B两点间的中点坐标.
答案:M(0,0,-3);A,B两点间的中点坐标(1,-1.5,1.5).
1.到定点(1,0,0)的距离小于或等于1的点的集
合是( )
A. {(x,y,z)|(x-1)2+y2+z2≤1}
B. {(x,y,z)|(x-1)2+y2+z2=1}
C. {(x,y,z)|x2+y2+z2≤2}
D. {(x,y,z)|x2+y2+z2≤1}
A
2.在Rt△ABC中,∠BAC=90°,三点的坐标为
A(2,1,1),B(1,1,2),C(x,0,1),则x=_____.
3.若点P(x,y,z)到A(1,0,1),B(2,1,0)两点的距离相等,则x、y、z满足的关系式
是________________.
2
2x+2y-2z-3=0
4.已知点P在z轴上满足|OP|=1(O是坐标原点),
则点P到点A(1,1,1)的距离是_________.
5.正方体不在同一平面上的两个顶点的坐标分别
为A(-1,2,-1),B(3,-2,3),则正方体的棱长
为_____.
4
一、两点间距离公式
类比
猜想
二、空间中点坐标公式
在空间直角坐标系中,点P(x1,y1,z1)和点Q(x2,y2,z2)的中点坐标(x,y,z):
三、学习本节内容涉及到的主要核心素养
1、迁移类别(平面两点之间的距离公式→空间两点之间的距离公式)
2、转化(空间问题→平面问题)
3、特殊到一般(先探究空间任意一点到原点的距离→空间任意两点之间的距离)
数学抽象 直观想象 数学运算 逻辑推理
方法使用:
不要害怕批评。当你提出新的观念时,就要准备接受别人的批评。
谢谢!!
课后作业:完成练习案及课后习题
