人教版八年级下数学18.2特殊的平行四边形复习学案(无答案)
文档属性
| 名称 | 人教版八年级下数学18.2特殊的平行四边形复习学案(无答案) | 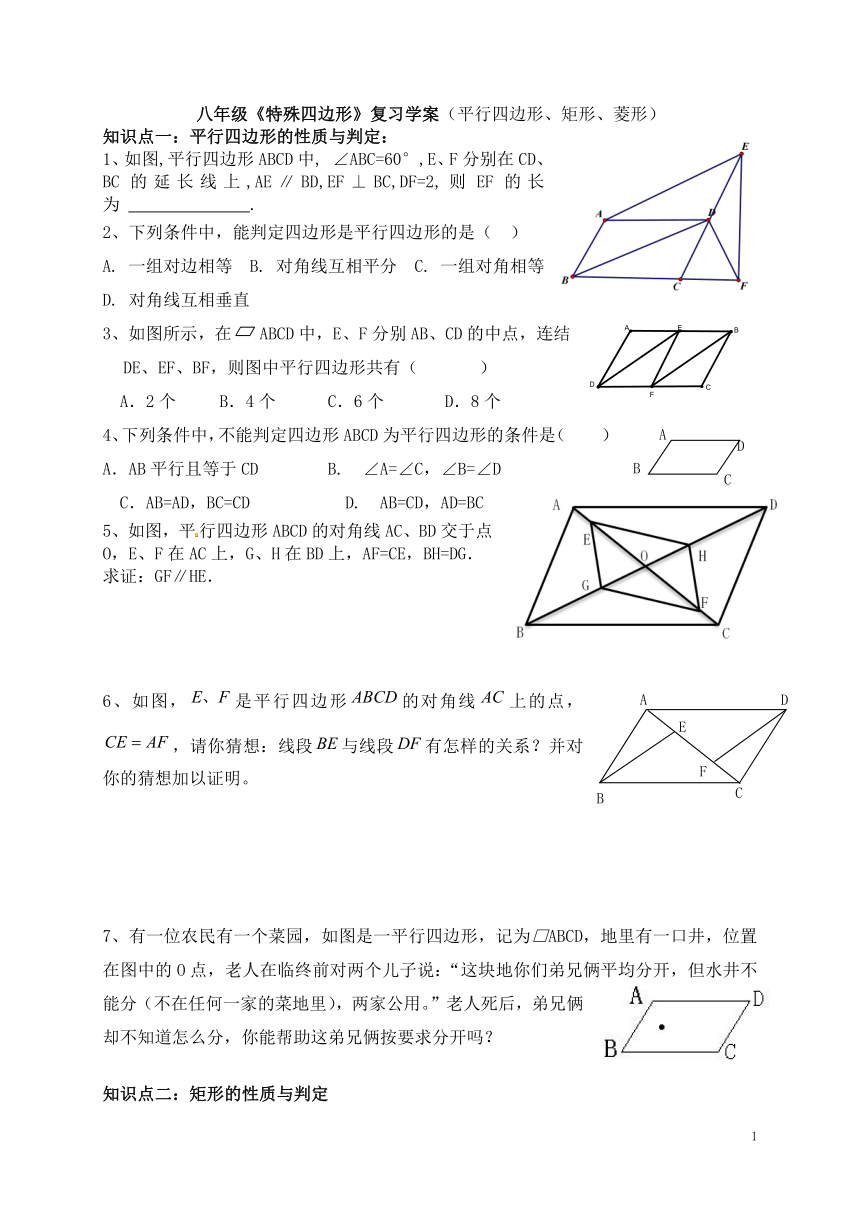 | |
| 格式 | zip | ||
| 文件大小 | 125.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-28 11:57:41 | ||
图片预览


文档简介
八年级《特殊四边形》复习学案(平行四边形、矩形、菱形)
知识点一:平行四边形的性质与判定:
1、如图,平行四边形ABCD中, ∠ABC=60°,E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BC,DF=2,则EF的长为 .
2、下列条件中,能判定四边形是平行四边形的是( )
A. 一组对边相等 B. 对角线互相平分 C. 一组对角相等 D. 对角线互相垂直
3、如图所示,在ABCD中,E、F分别AB、CD的中点,连结DE、EF、BF,则图中平行四边形共有( )
A.2个 B.4个 C.6个 D.8个
4、下列条件中,不能判定四边形ABCD为平行四边形的条件是( ) A.AB平行且等于CD B. ∠A=∠C,∠B=∠D
C.AB=AD,BC=CD D. AB=CD,AD=BC
5、如图,平行四边形ABCD的对角线AC、BD交于点O,E、F在AC上,G、H在BD上,AF=CE,BH=DG.
求证:GF∥HE.
6、如图,是平行四边形的对角线上的点,,请你猜想:线段与线段有怎样的关系?并对你的猜想加以证明。
7、有一位农民有一个菜园,如图是一平行四边形,记为□ABCD,地里有一口井,位置在图中的O点,老人在临终前对两个儿子说:“这块地你们弟兄俩平均分开,但水井不能分(不在任何一家的菜地里),两家公用。”老人死后,弟兄俩却不知道怎么分,你能帮助这弟兄俩按要求分开吗?
知识点二:矩形的性质与判定
◆知识讲解归纳
一、矩形的定义:有一个角是 的平行四边形叫做矩形.
二、矩形的性质:矩形是特殊的平行四边形,它除具有一般平行四边形的性之外,还具有(1)矩形的四个角都是 . (2)矩形的对角线 .
三、议一议:矩形ABCD的对角线AC与BD相交于点O,那么BO是Rt⊿ABC中一条怎样的特殊线段?它与AC有怎样的大小关系?为什么有这样的大小关系?因此,我们得到一个性质定理的推论:
直角三角形斜边上的中线等于 .
四、矩形的判定方法:(1)有一个角是 的平行四边形叫做矩形.
(2)对角线_________的平行四边形是矩形.(3)有三个角是________的四边形是矩形.
◆对应练习:
1、 一矩形两对角线之间的夹角有一个是600, 且这角所对的边长5cm,
则对角线长为 ( ) A. 5 cm B. 10cm C. 5cm D. 无法确定
2、如图在矩形ABCD中,对角线AC、BD相交于点O,则以下说法错误的是( )
A.AB=AD B.AC=BD
C. D.AO=OC=BO=OD
3、如图,矩形ABCD中,AB=3,BC=4,P是边AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为:_________。
4、矩形一个角的平分线分矩形一边成2cm和3cm,则这个矩形的面积为 。
5、如图,在矩形ABCD中,M是BC的中点,且MA⊥MD.若矩形ABCD的周长为48cm,求矩形ABCD的面积。
6、如图,在矩形ABCD中,已知AB=8cm,BC=10cm,折叠矩形的一边AD,使点D落在BC边的中点F处,折痕为AE,求CE的长.
7、如图,在矩形ABCD中,AE平分∠BAD,∠1=15°.
(1)求∠2的度数.(2)求证:BO=BE.
知识点三:菱形的性质与判定
◆知识讲解归纳
1.菱形的概念:一组 相等的平行四边形叫做菱形.
2.菱形的性质:边: ;
角: ;
对角线: 。
对称性 : 。
3.菱形的面积:⑴ ;⑵ 。
4.菱形的判定:(1).四条边都相等的_____________是菱形.
(2).邻边相等的_____________是菱形.
(3).对角线互相垂直的______________是菱形
对应练习:
1、如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )
A、16 B、17 C、18 D、19
2、如图,菱形ABCD的周长为16,∠A=60o,则对角线BD的长度是( )A.2 B.2 C.4 D.4
3.菱形的边长为5,一条对角线长为8,那么它的另一条对角线长为________
4.已知菱形的两条对角线的长分别为4cm,8cm,那么边长为_________
5.已知菱形的周长为40cm,两条对角线的长度比为3:4,那么两条对角线的长分别为( )A.6cm,8cm B. 3cm,4cm C. 12cm,16cm D. 24cm,32cm
6.在下列性质中,平行四边形具有的是_______________,菱形具有的是_____________,矩形具有的 是 ,正方形具有的是 。
四条边都相等; (2)对角线互相平分; (3)对角线相等;(4)对角线互相垂直; (5)四个角都是直角; (6)每一条对角线平分一组对角; (7)对边相等且平行; (8)有两条对称轴;
7.已知菱形的两条对角线的长分别为10cm与24cm,则边长为________,此菱形的面积为_________。
8.在□ABCD中,AC=21cm,BE⊥AC于E,且 BE=5cm,AD=7cm,则两平行线AD与BC间的距离是________________。
9.一个四边形边长依次是a、b、c、d,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形为:____________。
10.菱形有一个内角为60°,较短的对角线长为6cm,则菱形的边长为________,另一条对角线的长为___________。
11. 如图,将两张长为8,宽为2的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值 ,菱形周长的最大值是 .
12.如图,在ABCD中,O是对角线AC的中点,过点O作AC的垂线与边AD、BC分别交于E、F。求证:四边形AFCE是菱形。
13.(6分)如图,在□ABCD中,平分交于点,平分交于点.
求证:(1);
(2)若,则判断四边形是什么特殊四边形,请证明你的结论。
知识点一:平行四边形的性质与判定:
1、如图,平行四边形ABCD中, ∠ABC=60°,E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BC,DF=2,则EF的长为 .
2、下列条件中,能判定四边形是平行四边形的是( )
A. 一组对边相等 B. 对角线互相平分 C. 一组对角相等 D. 对角线互相垂直
3、如图所示,在ABCD中,E、F分别AB、CD的中点,连结DE、EF、BF,则图中平行四边形共有( )
A.2个 B.4个 C.6个 D.8个
4、下列条件中,不能判定四边形ABCD为平行四边形的条件是( ) A.AB平行且等于CD B. ∠A=∠C,∠B=∠D
C.AB=AD,BC=CD D. AB=CD,AD=BC
5、如图,平行四边形ABCD的对角线AC、BD交于点O,E、F在AC上,G、H在BD上,AF=CE,BH=DG.
求证:GF∥HE.
6、如图,是平行四边形的对角线上的点,,请你猜想:线段与线段有怎样的关系?并对你的猜想加以证明。
7、有一位农民有一个菜园,如图是一平行四边形,记为□ABCD,地里有一口井,位置在图中的O点,老人在临终前对两个儿子说:“这块地你们弟兄俩平均分开,但水井不能分(不在任何一家的菜地里),两家公用。”老人死后,弟兄俩却不知道怎么分,你能帮助这弟兄俩按要求分开吗?
知识点二:矩形的性质与判定
◆知识讲解归纳
一、矩形的定义:有一个角是 的平行四边形叫做矩形.
二、矩形的性质:矩形是特殊的平行四边形,它除具有一般平行四边形的性之外,还具有(1)矩形的四个角都是 . (2)矩形的对角线 .
三、议一议:矩形ABCD的对角线AC与BD相交于点O,那么BO是Rt⊿ABC中一条怎样的特殊线段?它与AC有怎样的大小关系?为什么有这样的大小关系?因此,我们得到一个性质定理的推论:
直角三角形斜边上的中线等于 .
四、矩形的判定方法:(1)有一个角是 的平行四边形叫做矩形.
(2)对角线_________的平行四边形是矩形.(3)有三个角是________的四边形是矩形.
◆对应练习:
1、 一矩形两对角线之间的夹角有一个是600, 且这角所对的边长5cm,
则对角线长为 ( ) A. 5 cm B. 10cm C. 5cm D. 无法确定
2、如图在矩形ABCD中,对角线AC、BD相交于点O,则以下说法错误的是( )
A.AB=AD B.AC=BD
C. D.AO=OC=BO=OD
3、如图,矩形ABCD中,AB=3,BC=4,P是边AD上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为:_________。
4、矩形一个角的平分线分矩形一边成2cm和3cm,则这个矩形的面积为 。
5、如图,在矩形ABCD中,M是BC的中点,且MA⊥MD.若矩形ABCD的周长为48cm,求矩形ABCD的面积。
6、如图,在矩形ABCD中,已知AB=8cm,BC=10cm,折叠矩形的一边AD,使点D落在BC边的中点F处,折痕为AE,求CE的长.
7、如图,在矩形ABCD中,AE平分∠BAD,∠1=15°.
(1)求∠2的度数.(2)求证:BO=BE.
知识点三:菱形的性质与判定
◆知识讲解归纳
1.菱形的概念:一组 相等的平行四边形叫做菱形.
2.菱形的性质:边: ;
角: ;
对角线: 。
对称性 : 。
3.菱形的面积:⑴ ;⑵ 。
4.菱形的判定:(1).四条边都相等的_____________是菱形.
(2).邻边相等的_____________是菱形.
(3).对角线互相垂直的______________是菱形
对应练习:
1、如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )
A、16 B、17 C、18 D、19
2、如图,菱形ABCD的周长为16,∠A=60o,则对角线BD的长度是( )A.2 B.2 C.4 D.4
3.菱形的边长为5,一条对角线长为8,那么它的另一条对角线长为________
4.已知菱形的两条对角线的长分别为4cm,8cm,那么边长为_________
5.已知菱形的周长为40cm,两条对角线的长度比为3:4,那么两条对角线的长分别为( )A.6cm,8cm B. 3cm,4cm C. 12cm,16cm D. 24cm,32cm
6.在下列性质中,平行四边形具有的是_______________,菱形具有的是_____________,矩形具有的 是 ,正方形具有的是 。
四条边都相等; (2)对角线互相平分; (3)对角线相等;(4)对角线互相垂直; (5)四个角都是直角; (6)每一条对角线平分一组对角; (7)对边相等且平行; (8)有两条对称轴;
7.已知菱形的两条对角线的长分别为10cm与24cm,则边长为________,此菱形的面积为_________。
8.在□ABCD中,AC=21cm,BE⊥AC于E,且 BE=5cm,AD=7cm,则两平行线AD与BC间的距离是________________。
9.一个四边形边长依次是a、b、c、d,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形为:____________。
10.菱形有一个内角为60°,较短的对角线长为6cm,则菱形的边长为________,另一条对角线的长为___________。
11. 如图,将两张长为8,宽为2的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值 ,菱形周长的最大值是 .
12.如图,在ABCD中,O是对角线AC的中点,过点O作AC的垂线与边AD、BC分别交于E、F。求证:四边形AFCE是菱形。
13.(6分)如图,在□ABCD中,平分交于点,平分交于点.
求证:(1);
(2)若,则判断四边形是什么特殊四边形,请证明你的结论。
