人教版八年级下数学18.1.2平行四边形判定课件(第二课时 24张)
文档属性
| 名称 | 人教版八年级下数学18.1.2平行四边形判定课件(第二课时 24张) |  | |
| 格式 | zip | ||
| 文件大小 | 205.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-29 21:01:47 | ||
图片预览



文档简介
课件24张PPT。zx``x```k18.1.2 平行四边形的判定
第2课时
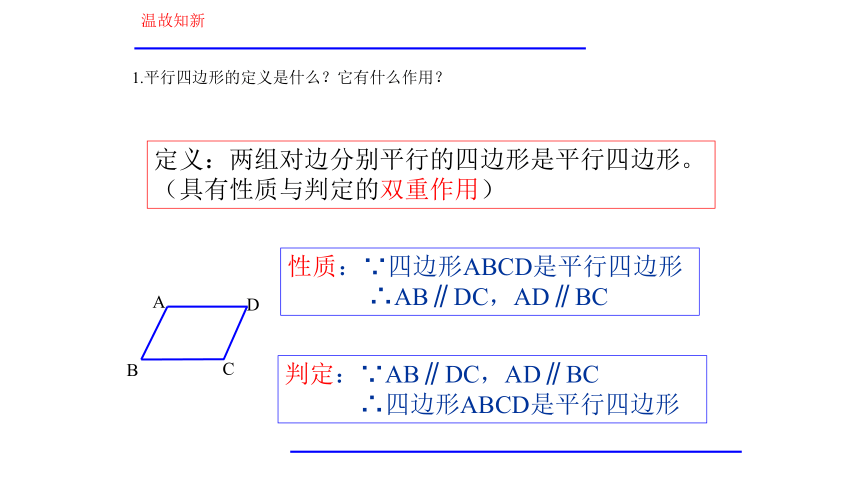
第十八章 平行四边形第18章 平行四边形 1.平行四边形的定义是什么?它有什么作用?温故知新定义:两组对边分别平行的四边形是平行四边形。 (具有性质与判定的双重作用)性质:∵四边形ABCD是平行四边形
∴AB∥DC,AD∥BC判定:∵AB∥DC,AD∥BC
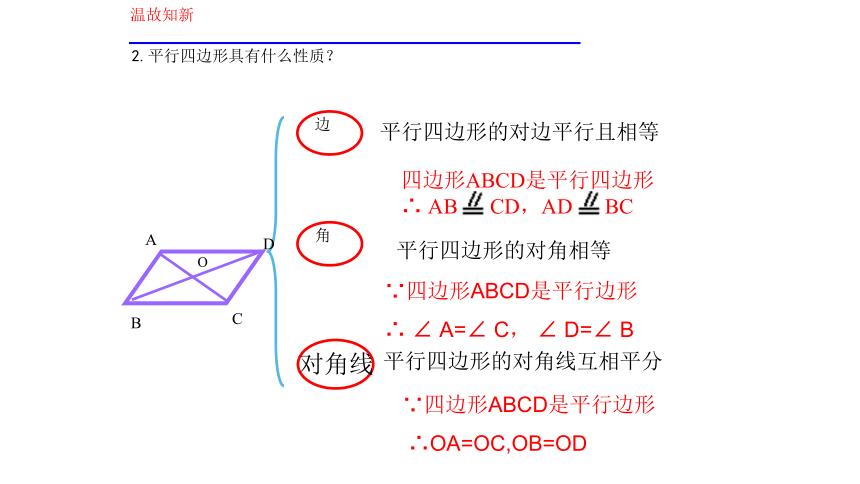
∴四边形ABCD是平行四边形2.平行四边形具有什么性质?温故知新平行四边形的对边平行且相等 平行四边形的对角线互相平分O平行四边形的对角相等∵四边形ABCD是平行边形
∴OA=OC,OB=OD∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B符号表示:∵AB∥DC,AD∥BC
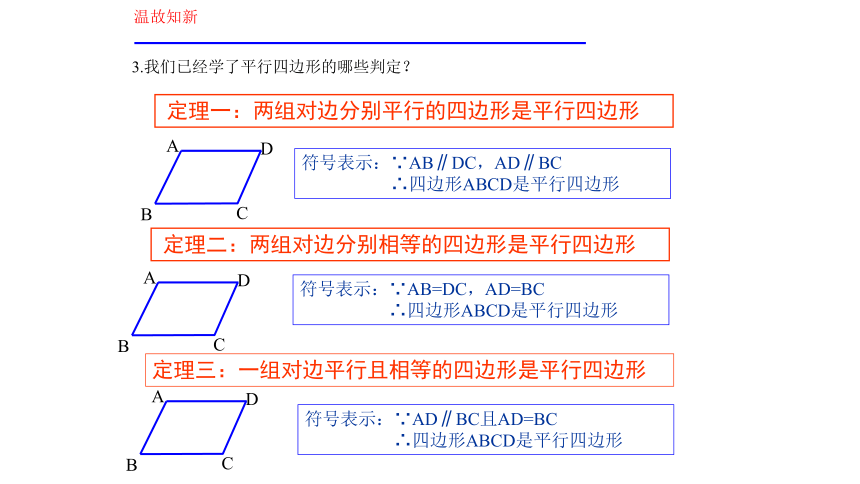
∴四边形ABCD是平行四边形定理三:一组对边平行且相等的四边形是平行四边形 定理二:两组对边分别相等的四边形是平行四边形符号表示:∵AD∥BC且AD=BC
∴四边形ABCD是平行四边形温故知新 3.我们已经学了平行四边形的哪些判定? 定理一:两组对边分别平行的四边形是平行四边形符号表示:∵AB=DC,AD=BC
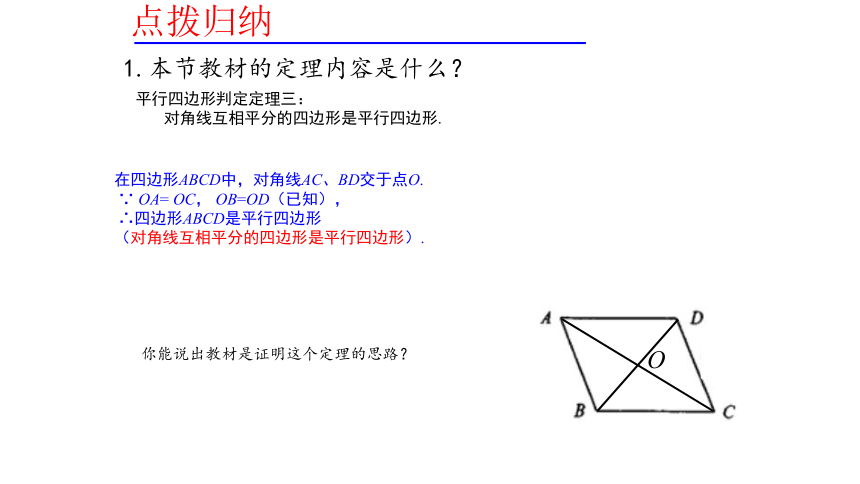
∴四边形ABCD是平行四边形猜——反过来,由平行四边形边、角、对角线之间的关系,你能得出平行四边形的判定方法吗?对角线互相平分的四边形是平行四边形吗?两组对角相等的四边形是平行四边形吗?自主学习学材第143页到144页,并思考下列问题.(12分钟)自主学习11.本节教材的定理内容是什么?你能说出教材证明这个定理的思路?2.你能简要分析例2的证明思路吗?3.两组对角相等的四边形是平行四边形吗?请说明理由.完成随堂练习和习题6.4的1、2题,平行四边形判定定理三:
对角线互相平分的四边形是平行四边形.在四边形ABCD中,对角线AC、BD交于点O.
∵ OA= OC, OB=OD(已知),
∴四边形ABCD是平行四边形
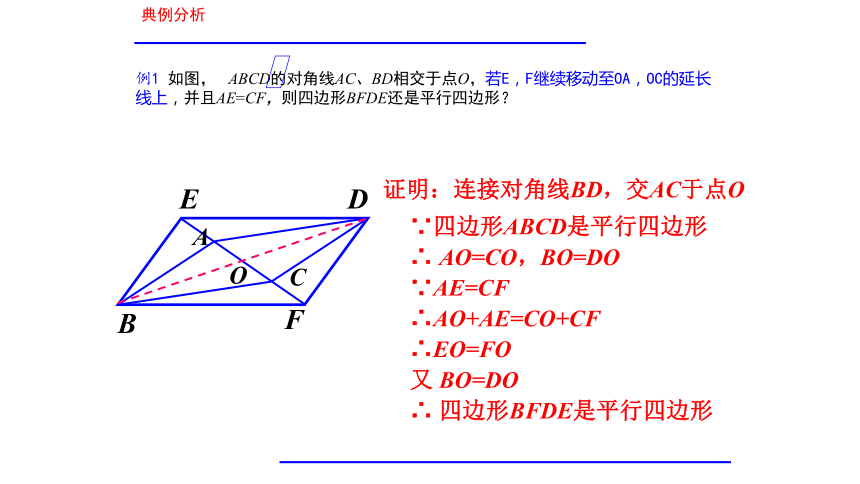
(对角线互相平分的四边形是平行四边形).点拨归纳1.本节教材的定理内容是什么?你能说出教材是证明这个定理的思路?典例分析证明:连接对角线BD,交AC于点O ∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO+AE=CO+CF
∴EO=FO
又 BO=DO
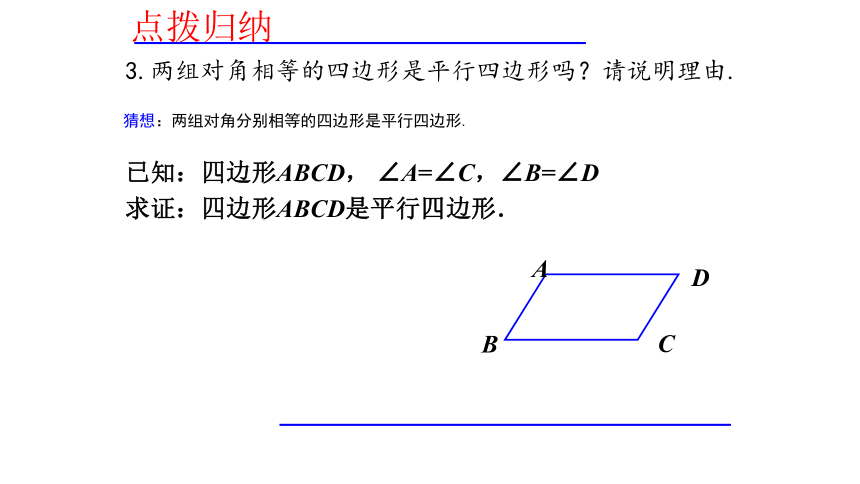
∴ 四边形BFDE是平行四边形O猜想:两组对角分别相等的四边形是平行四边形.点拨归纳3.两组对角相等的四边形是平行四边形吗?请说明理由.已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形.
证明:∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)同理可证AB∥CD又∵∠A+ ∠B+ ∠C+ ∠D =360 °∴ 2∠A+ 2∠B=360 °∵∠A=∠C,∠B=∠D(已知)即∠A+ ∠B=180 °∴ AD∥BC (同旁内角互补,两直线平行)已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形.平行四边形判定定理四:
两组对角分别相等的四边形是平行四边形.在四边形ABCD中,
∵ ∠A= ∠C, ∠B= ∠D
∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形).点拨归纳1 如图,在 ABCD中,已知两条对角线相交于O点,点E、F分别是AO、CO的中点,四边形BFDE是平行四边形吗?请说明理由.ADCB自捡互评 解:四边形BFDE是平行四边
理由如下:
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵ E、F分别是AO、CO的中点
∴OE= AO,OF= OC
∴OE=OF
又 ∵BO=DO
∴ 四边形BFDE是平行四边形2、已知:如图,AC是 ABCD中,且BM⊥AC于M,DN⊥AC于N.求证:四边形BEDF是平行四边形. 证明:(方法一)
∵ 四边形ABCD是平行四边形,
∴ AB=CD,且AB∥CD.
∴ ∠BAM=∠DCN.
∵ BM⊥AC于M,DN⊥AC于N,
∴ BM∥DN,∠BMA=∠DNC=90°
在△ABM和△CDN中
∴ △ABM≌△CDN(AAS).
∠BMA=∠DNC
∠BAM=∠DCN
AB=CD∴ BM=DN.
∴ 四边形BNDM是平行四边形2、已知:如图,AC是 ABCD中,且BM⊥AC于M,DN⊥AC于N.求证:四边形BEDF是平行四边形. 证明:(方法二)
∵ 四边形ABCD是平行四边形,
∴ OB=OD.
∵ BM⊥AC于M,DN⊥AC于N,
∴ ∠BMO=∠DNO=90°
在△AOM和△DON中
∴ △AOM≌△DON(AAS).
∠BMO=∠DNO
∠BOM=∠DON
OB=OD ∴ OM=ON.
∵OB=OD
∴ 四边形BNDM是平行四边形O3、如图, ABCD中,对角线AC、BD相交于点O,E、F、G、H分别是OA、OC、OB、OD的中点,四边形EGFH平行四边形?请说明理由.C解决教材145页的问题解决 3证明:∵ 四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
∵ E、F分别是AD、BC的中点,
∴ OE= AO,OF= OC
∴ OE=OF.
同理可得OG=OH
∴ 四边形GEHF是平行四边形(对角线互相平分的四边形是平行四边形).如图,在 ABCD中,已知两条对角线相交于
点O,E、F、G、H分别是AO、BO、CO、DO的中点,
以图中的点为顶点,尽可能多地画出平行四边形。ADCBEFGHO拓展四、知识总结 我们学了哪些判定四边形是平行四边形的方法?平行四边形的判定两组对边分别平行的四边形对角线互相平分的四边形两组对边分别相等的四边形一组对边平行且相等的四边形两组对角分别相等的四边形知识网络图平行四边形的性质:平行四边形的对边平行平行四边形的对边相等平行四边形的对角相等平行四边形的邻角互补平行四边形的对角线互相平分ABCD自主学习学材第146页到148页,并思考下列问题.(12分钟)自主学习21.什么是平行线间的距离?2.夹在平行线间的平行线段有何特点,你是怎样得到结论的?完成随堂练习和习题6.5点拨归纳21.什么是平行线间的距离?2.夹在平行线间的平行线段有何特点,你是怎样得到结论的?平行线间的线段的性质:
(1)平行线间的距离处处相等;
(2)夹在平行线间的平行线段的长度相等。典例分析1.已知 L1∥L2∥L3,相邻两条平行线间的距离等于1,若等腰直角三角形ABC的三个顶点分别在这三条平行线上,求AB的长
ACBL1L2L3典例分析2.已知平行四边形ABCD,过A作AM⊥BC于点M,
过C作CN⊥AD于点N,分别交BD于E、F,连接AF、CE.
求证;四边形AECF为平行四边形
第2课时
第十八章 平行四边形第18章 平行四边形 1.平行四边形的定义是什么?它有什么作用?温故知新定义:两组对边分别平行的四边形是平行四边形。 (具有性质与判定的双重作用)性质:∵四边形ABCD是平行四边形
∴AB∥DC,AD∥BC判定:∵AB∥DC,AD∥BC
∴四边形ABCD是平行四边形2.平行四边形具有什么性质?温故知新平行四边形的对边平行且相等 平行四边形的对角线互相平分O平行四边形的对角相等∵四边形ABCD是平行边形
∴OA=OC,OB=OD∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B符号表示:∵AB∥DC,AD∥BC
∴四边形ABCD是平行四边形定理三:一组对边平行且相等的四边形是平行四边形 定理二:两组对边分别相等的四边形是平行四边形符号表示:∵AD∥BC且AD=BC
∴四边形ABCD是平行四边形温故知新 3.我们已经学了平行四边形的哪些判定? 定理一:两组对边分别平行的四边形是平行四边形符号表示:∵AB=DC,AD=BC
∴四边形ABCD是平行四边形猜——反过来,由平行四边形边、角、对角线之间的关系,你能得出平行四边形的判定方法吗?对角线互相平分的四边形是平行四边形吗?两组对角相等的四边形是平行四边形吗?自主学习学材第143页到144页,并思考下列问题.(12分钟)自主学习11.本节教材的定理内容是什么?你能说出教材证明这个定理的思路?2.你能简要分析例2的证明思路吗?3.两组对角相等的四边形是平行四边形吗?请说明理由.完成随堂练习和习题6.4的1、2题,平行四边形判定定理三:
对角线互相平分的四边形是平行四边形.在四边形ABCD中,对角线AC、BD交于点O.
∵ OA= OC, OB=OD(已知),
∴四边形ABCD是平行四边形
(对角线互相平分的四边形是平行四边形).点拨归纳1.本节教材的定理内容是什么?你能说出教材是证明这个定理的思路?典例分析证明:连接对角线BD,交AC于点O ∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO+AE=CO+CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形O猜想:两组对角分别相等的四边形是平行四边形.点拨归纳3.两组对角相等的四边形是平行四边形吗?请说明理由.已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形.
证明:∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)同理可证AB∥CD又∵∠A+ ∠B+ ∠C+ ∠D =360 °∴ 2∠A+ 2∠B=360 °∵∠A=∠C,∠B=∠D(已知)即∠A+ ∠B=180 °∴ AD∥BC (同旁内角互补,两直线平行)已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形.平行四边形判定定理四:
两组对角分别相等的四边形是平行四边形.在四边形ABCD中,
∵ ∠A= ∠C, ∠B= ∠D
∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形).点拨归纳1 如图,在 ABCD中,已知两条对角线相交于O点,点E、F分别是AO、CO的中点,四边形BFDE是平行四边形吗?请说明理由.ADCB自捡互评 解:四边形BFDE是平行四边
理由如下:
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵ E、F分别是AO、CO的中点
∴OE= AO,OF= OC
∴OE=OF
又 ∵BO=DO
∴ 四边形BFDE是平行四边形2、已知:如图,AC是 ABCD中,且BM⊥AC于M,DN⊥AC于N.求证:四边形BEDF是平行四边形. 证明:(方法一)
∵ 四边形ABCD是平行四边形,
∴ AB=CD,且AB∥CD.
∴ ∠BAM=∠DCN.
∵ BM⊥AC于M,DN⊥AC于N,
∴ BM∥DN,∠BMA=∠DNC=90°
在△ABM和△CDN中
∴ △ABM≌△CDN(AAS).
∠BMA=∠DNC
∠BAM=∠DCN
AB=CD∴ BM=DN.
∴ 四边形BNDM是平行四边形2、已知:如图,AC是 ABCD中,且BM⊥AC于M,DN⊥AC于N.求证:四边形BEDF是平行四边形. 证明:(方法二)
∵ 四边形ABCD是平行四边形,
∴ OB=OD.
∵ BM⊥AC于M,DN⊥AC于N,
∴ ∠BMO=∠DNO=90°
在△AOM和△DON中
∴ △AOM≌△DON(AAS).
∠BMO=∠DNO
∠BOM=∠DON
OB=OD ∴ OM=ON.
∵OB=OD
∴ 四边形BNDM是平行四边形O3、如图, ABCD中,对角线AC、BD相交于点O,E、F、G、H分别是OA、OC、OB、OD的中点,四边形EGFH平行四边形?请说明理由.C解决教材145页的问题解决 3证明:∵ 四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
∵ E、F分别是AD、BC的中点,
∴ OE= AO,OF= OC
∴ OE=OF.
同理可得OG=OH
∴ 四边形GEHF是平行四边形(对角线互相平分的四边形是平行四边形).如图,在 ABCD中,已知两条对角线相交于
点O,E、F、G、H分别是AO、BO、CO、DO的中点,
以图中的点为顶点,尽可能多地画出平行四边形。ADCBEFGHO拓展四、知识总结 我们学了哪些判定四边形是平行四边形的方法?平行四边形的判定两组对边分别平行的四边形对角线互相平分的四边形两组对边分别相等的四边形一组对边平行且相等的四边形两组对角分别相等的四边形知识网络图平行四边形的性质:平行四边形的对边平行平行四边形的对边相等平行四边形的对角相等平行四边形的邻角互补平行四边形的对角线互相平分ABCD自主学习学材第146页到148页,并思考下列问题.(12分钟)自主学习21.什么是平行线间的距离?2.夹在平行线间的平行线段有何特点,你是怎样得到结论的?完成随堂练习和习题6.5点拨归纳21.什么是平行线间的距离?2.夹在平行线间的平行线段有何特点,你是怎样得到结论的?平行线间的线段的性质:
(1)平行线间的距离处处相等;
(2)夹在平行线间的平行线段的长度相等。典例分析1.已知 L1∥L2∥L3,相邻两条平行线间的距离等于1,若等腰直角三角形ABC的三个顶点分别在这三条平行线上,求AB的长
ACBL1L2L3典例分析2.已知平行四边形ABCD,过A作AM⊥BC于点M,
过C作CN⊥AD于点N,分别交BD于E、F,连接AF、CE.
求证;四边形AECF为平行四边形
