人教版八年级下数学18.1.1平行四边形性质教案
文档属性
| 名称 | 人教版八年级下数学18.1.1平行四边形性质教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 114.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-29 21:05:32 | ||
图片预览



文档简介
18.1.1平行四边形的性质
教学目标:
1.掌握平行四边形的定义、性质,能根据性质解决简单问题,培养合情推理能力;
2.经历观察、猜想、实践、验证的数学活动,逐步建立类比、转化的数学思想,获得证明线段相等和角相等的新的数学方法;
3.在探索平行四边形性质的过程中培养学生的合作探究意识和独立思考的习惯,使学生在数学学习活动中获得成功的体验,感受数学美.
教学重点:平行四边形性质的探究,平行四边形性质的应用.
教学难点:平行四边形性质的探究
教学方法:引导发现法、实验操作法
教学过程:
教学流程
教师活动
学生活动
第一环节
创设情境
发现性质
创设情境 发现性质----做生活的有心人
善于观察的喜羊羊
教师出示喜羊羊的图片,提出问题:同学们,认识他吗?喜羊羊可是生活的有心人,他善于观察生活,还注意收集生活中的图案。你能从喜羊羊收集的图片中找出我们熟悉的几何图形吗?
你能说出平行四边形的定义吗?
有两组对边分别平行的四边形叫做平行四边形
强调:①两组对边分别平行②四边形
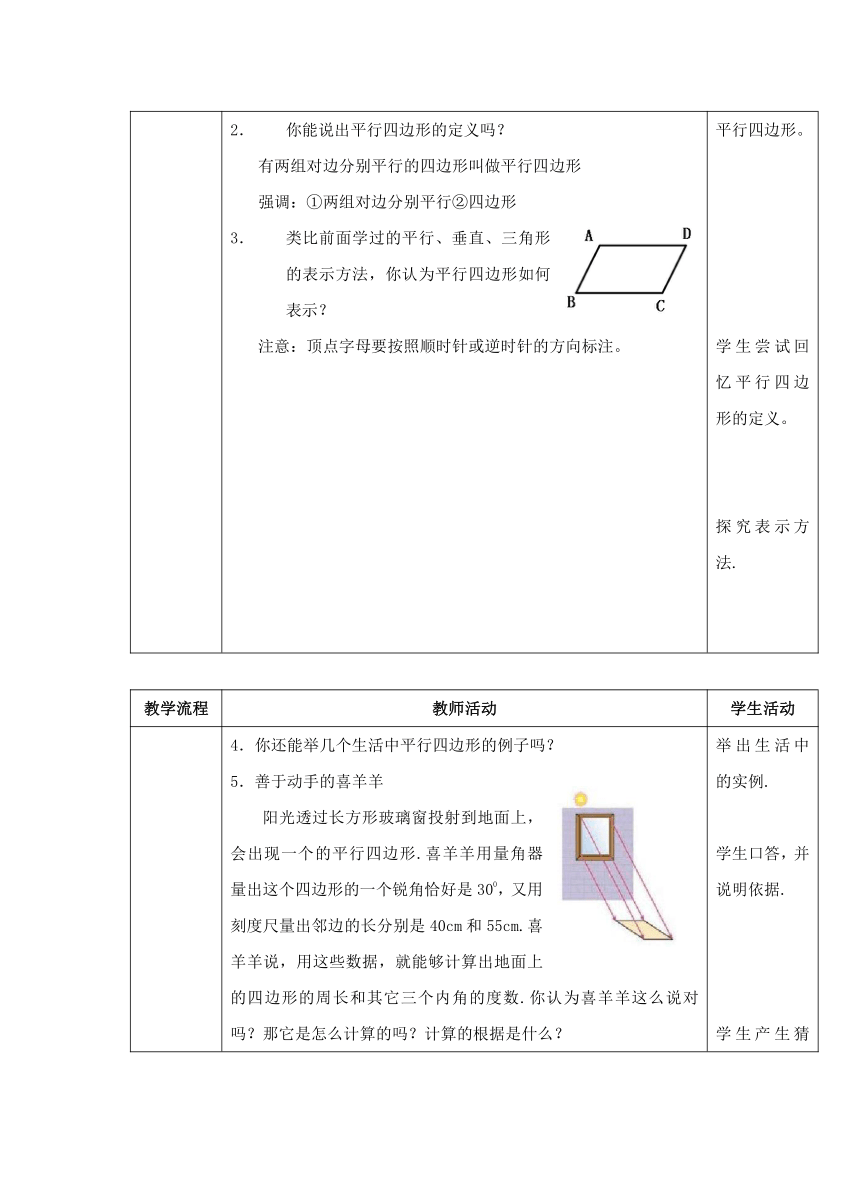
类比前面学过的平行、垂直、三角形的表示方法,你认为平行四边形如何表示?
注意:顶点字母要按照顺时针或逆时针的方向标注。
学生欣赏喜羊羊收集的图片,找出学过的几何图形.
感受生活中存在大量的平行四边形。
学生尝试回忆平行四边形的定义。
探究表示方法.
教学流程
教师活动
学生活动
4.你还能举几个生活中平行四边形的例子吗?
5.善于动手的喜羊羊
阳光透过长方形玻璃窗投射到地面上,会出现一个的平行四边形.喜羊羊用量角器量出这个四边形的一个锐角恰好是300,又用刻度尺量出邻边的长分别是40cm和55cm.喜羊羊说,用这些数据,就能够计算出地面上的四边形的周长和其它三个内角的度数.你认为喜羊羊这么说对吗?那它是怎么计算的吗?计算的根据是什么?
举出生活中的实例.
学生口答,并说明依据.
学生产生猜想。
第二环节
动手操作
验证性质
动手操作 验证性质----做善于动手的人
1.你能利用手中的学具检验你的猜想正确吗?先独立验证,然后在小组内交流你的方法。
估计学生可能采用的方法:
用刻度尺量出线段的长度、用量角器量出角的度数
把平行四边形剪成两个全等的三角形
值得一提的是学生不仅仅采用了上面的方法,一些小组还采用了以下的方法:
把平行四边形剪成了两个平行四边形,然后重合两个对角。
把平行四边形叠成一个圆柱,验证对边相等。
利用几何画板软件,测量平行四边形的边长和四个角的角度。
学生观察和猜想得出结论。
运用手中的学具检验猜想是否正确。
小组合作交流检验方法和结果。
教学流程
教师活动
学生活动
第三环节
合作探究
证明性质
合作探究 证明性质----做思维严谨的人
猜想1 平行四边形的对角相等
1.写出已知、求证.
2.先独立思考,然后在小组内交流你的方法。
教师估计:学生在证明角相等时,可能会想到利用同旁内角,但是对于辅助线的加法和解决问题的思路分析可能比较模糊。
值得一提的是,学生在证明时想到了多种证法:
用同旁内角来证。
利用同位角和内错角来证。
分割成两个平行四边形来证。
(4)分割成两个全等三角形来证。
辅助线如下:
3.通过刚才的证明,你有什么体会?
4.符号表示:
∵四边形ABCD为平行四边形 ∴_______
5. 若四边形ABCD为平行四边形
(1)则∠A:∠B:∠C:∠D=2:1:__:___
(2)∠B=600,则∠A=____ ,∠C=____,∠D=____
(3)∠B+∠D=1100,则∠A=____,∠C=____,∠D=___
(4)∠C-∠B=400,则∠A=___,C=____,∠D=___
猜想2 平行四边形的对边相等
1.写出已知、求证.
2.你会证明吗?你有什么体会?
3.符号表示:
∵四边形ABCD为平行四边形 ∴____________________
4.若四边形ABCD为平行四边形,
(1)若AB=10,BC=15,则AD= ,CD= ,周长为 .
(2)若周长为40,AB=12,则BC= ,AD= ,CD= .
(3)若周长为40,BC比AB长4,则AB= ,BC= .
学生独立思考、组内交流、全班展示。
学生尝试解答学生先独立思考,再在小组内交流证明的方法,然后全班展示。
学生总结归纳(动手操作为推理证明提供了加辅助线的方法和解决问题思路)。
文字语言转化为符号语言。
学生尝试解答。
学生尝试证明
学生练习
教学流程
教师活动
学生活动
第四环节
典型例题 应用性质
典型例题 应用性质——做善于应用的人
情景回顾:已知:平行四边形ABCD,∠B=300,AB=40,BC=55,求平行四边形ABCD的周长和面积。
例题:如图小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三边长分别为多少?
学生尝试解答。
第五环节
题组训练
巩固性质
题组训练 巩固性质——做再接再厉的人
看谁答的快!
如图,四边形ABCD是平行四边形
1)若CD=6 ㎝,则AB=_____㎝。
2)若∠A=70°,则∠B=___,∠C=_____。
3)若∠A+∠C=80°,则∠D=____。
小试牛刀
如图:在平行四边形ABCD中,AC为对角线,E、F分别为对角线AC上的两点,AE=CF,求证:BE=DF
学生抢答。
学生尝试证明。
第六环节
总结反思获得升华
总结反思 获得升华——做勤于反思的人
通过本节课的学习:
我学会了……
我还想知道……
学生交流汇报本节课的收获、体会.
布置作业 课外拓展
必做题:教科书第84页练习第1、2、3题.
选做题:1.试探索平行四边形的其他性质.
2.利用平行四边形设计美丽图案,表达你的美好
愿望.
学生作业。
板书设计
平行四边形的性质
1.定义:两组对边分别平行的四边形叫做平行四边形
2.表示方法
3.性质:
平行四边形的对角相等
平行四边形的对边相等
例题:
观察
猜想
验证
证明
教学目标:
1.掌握平行四边形的定义、性质,能根据性质解决简单问题,培养合情推理能力;
2.经历观察、猜想、实践、验证的数学活动,逐步建立类比、转化的数学思想,获得证明线段相等和角相等的新的数学方法;
3.在探索平行四边形性质的过程中培养学生的合作探究意识和独立思考的习惯,使学生在数学学习活动中获得成功的体验,感受数学美.
教学重点:平行四边形性质的探究,平行四边形性质的应用.
教学难点:平行四边形性质的探究
教学方法:引导发现法、实验操作法
教学过程:
教学流程
教师活动
学生活动
第一环节
创设情境
发现性质
创设情境 发现性质----做生活的有心人
善于观察的喜羊羊
教师出示喜羊羊的图片,提出问题:同学们,认识他吗?喜羊羊可是生活的有心人,他善于观察生活,还注意收集生活中的图案。你能从喜羊羊收集的图片中找出我们熟悉的几何图形吗?
你能说出平行四边形的定义吗?
有两组对边分别平行的四边形叫做平行四边形
强调:①两组对边分别平行②四边形
类比前面学过的平行、垂直、三角形的表示方法,你认为平行四边形如何表示?
注意:顶点字母要按照顺时针或逆时针的方向标注。
学生欣赏喜羊羊收集的图片,找出学过的几何图形.
感受生活中存在大量的平行四边形。
学生尝试回忆平行四边形的定义。
探究表示方法.
教学流程
教师活动
学生活动
4.你还能举几个生活中平行四边形的例子吗?
5.善于动手的喜羊羊
阳光透过长方形玻璃窗投射到地面上,会出现一个的平行四边形.喜羊羊用量角器量出这个四边形的一个锐角恰好是300,又用刻度尺量出邻边的长分别是40cm和55cm.喜羊羊说,用这些数据,就能够计算出地面上的四边形的周长和其它三个内角的度数.你认为喜羊羊这么说对吗?那它是怎么计算的吗?计算的根据是什么?
举出生活中的实例.
学生口答,并说明依据.
学生产生猜想。
第二环节
动手操作
验证性质
动手操作 验证性质----做善于动手的人
1.你能利用手中的学具检验你的猜想正确吗?先独立验证,然后在小组内交流你的方法。
估计学生可能采用的方法:
用刻度尺量出线段的长度、用量角器量出角的度数
把平行四边形剪成两个全等的三角形
值得一提的是学生不仅仅采用了上面的方法,一些小组还采用了以下的方法:
把平行四边形剪成了两个平行四边形,然后重合两个对角。
把平行四边形叠成一个圆柱,验证对边相等。
利用几何画板软件,测量平行四边形的边长和四个角的角度。
学生观察和猜想得出结论。
运用手中的学具检验猜想是否正确。
小组合作交流检验方法和结果。
教学流程
教师活动
学生活动
第三环节
合作探究
证明性质
合作探究 证明性质----做思维严谨的人
猜想1 平行四边形的对角相等
1.写出已知、求证.
2.先独立思考,然后在小组内交流你的方法。
教师估计:学生在证明角相等时,可能会想到利用同旁内角,但是对于辅助线的加法和解决问题的思路分析可能比较模糊。
值得一提的是,学生在证明时想到了多种证法:
用同旁内角来证。
利用同位角和内错角来证。
分割成两个平行四边形来证。
(4)分割成两个全等三角形来证。
辅助线如下:
3.通过刚才的证明,你有什么体会?
4.符号表示:
∵四边形ABCD为平行四边形 ∴_______
5. 若四边形ABCD为平行四边形
(1)则∠A:∠B:∠C:∠D=2:1:__:___
(2)∠B=600,则∠A=____ ,∠C=____,∠D=____
(3)∠B+∠D=1100,则∠A=____,∠C=____,∠D=___
(4)∠C-∠B=400,则∠A=___,C=____,∠D=___
猜想2 平行四边形的对边相等
1.写出已知、求证.
2.你会证明吗?你有什么体会?
3.符号表示:
∵四边形ABCD为平行四边形 ∴____________________
4.若四边形ABCD为平行四边形,
(1)若AB=10,BC=15,则AD= ,CD= ,周长为 .
(2)若周长为40,AB=12,则BC= ,AD= ,CD= .
(3)若周长为40,BC比AB长4,则AB= ,BC= .
学生独立思考、组内交流、全班展示。
学生尝试解答学生先独立思考,再在小组内交流证明的方法,然后全班展示。
学生总结归纳(动手操作为推理证明提供了加辅助线的方法和解决问题思路)。
文字语言转化为符号语言。
学生尝试解答。
学生尝试证明
学生练习
教学流程
教师活动
学生活动
第四环节
典型例题 应用性质
典型例题 应用性质——做善于应用的人
情景回顾:已知:平行四边形ABCD,∠B=300,AB=40,BC=55,求平行四边形ABCD的周长和面积。
例题:如图小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三边长分别为多少?
学生尝试解答。
第五环节
题组训练
巩固性质
题组训练 巩固性质——做再接再厉的人
看谁答的快!
如图,四边形ABCD是平行四边形
1)若CD=6 ㎝,则AB=_____㎝。
2)若∠A=70°,则∠B=___,∠C=_____。
3)若∠A+∠C=80°,则∠D=____。
小试牛刀
如图:在平行四边形ABCD中,AC为对角线,E、F分别为对角线AC上的两点,AE=CF,求证:BE=DF
学生抢答。
学生尝试证明。
第六环节
总结反思获得升华
总结反思 获得升华——做勤于反思的人
通过本节课的学习:
我学会了……
我还想知道……
学生交流汇报本节课的收获、体会.
布置作业 课外拓展
必做题:教科书第84页练习第1、2、3题.
选做题:1.试探索平行四边形的其他性质.
2.利用平行四边形设计美丽图案,表达你的美好
愿望.
学生作业。
板书设计
平行四边形的性质
1.定义:两组对边分别平行的四边形叫做平行四边形
2.表示方法
3.性质:
平行四边形的对角相等
平行四边形的对边相等
例题:
观察
猜想
验证
证明
