教师辅导讲义
学员编号： 年 级： 课 时 数： 学员姓名： 辅导科目： 学科教师：
授课类型 T（二次函数图像题）
授课日期及时段
教学内容
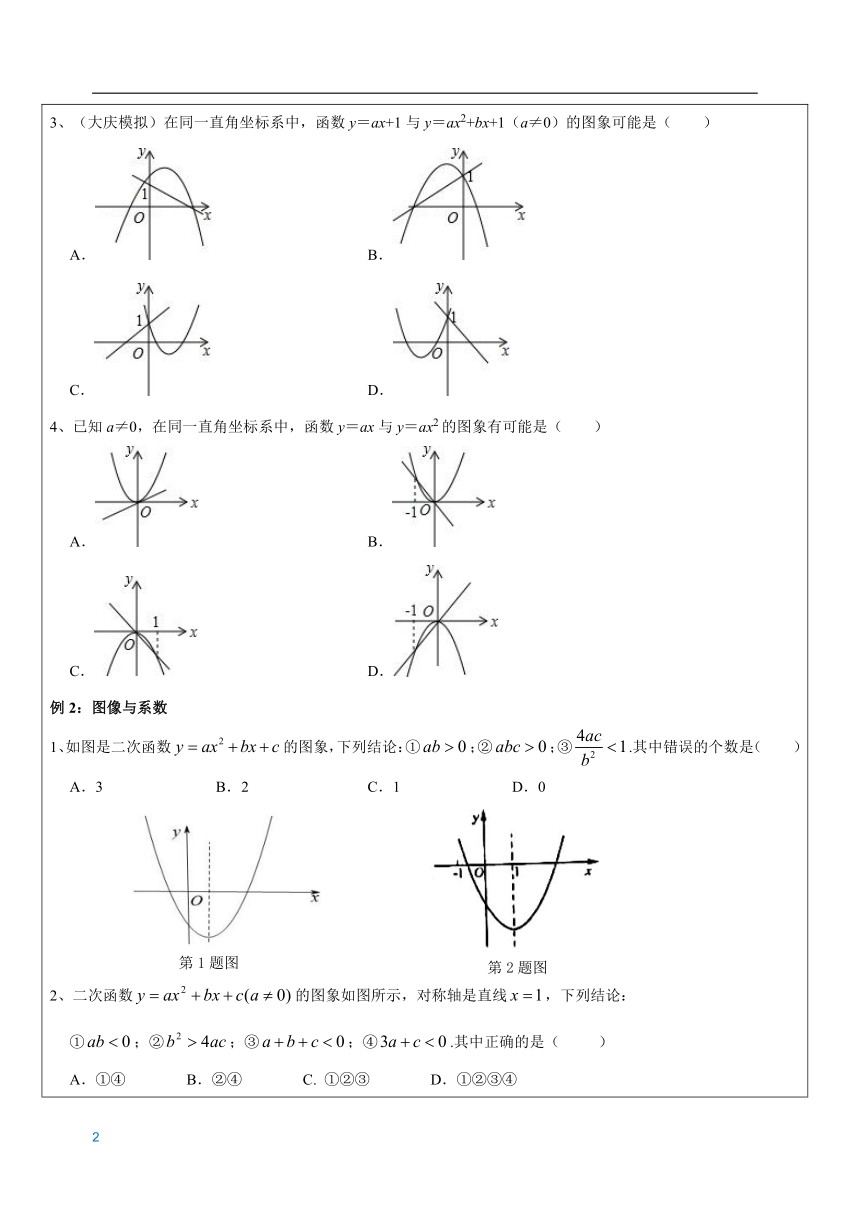
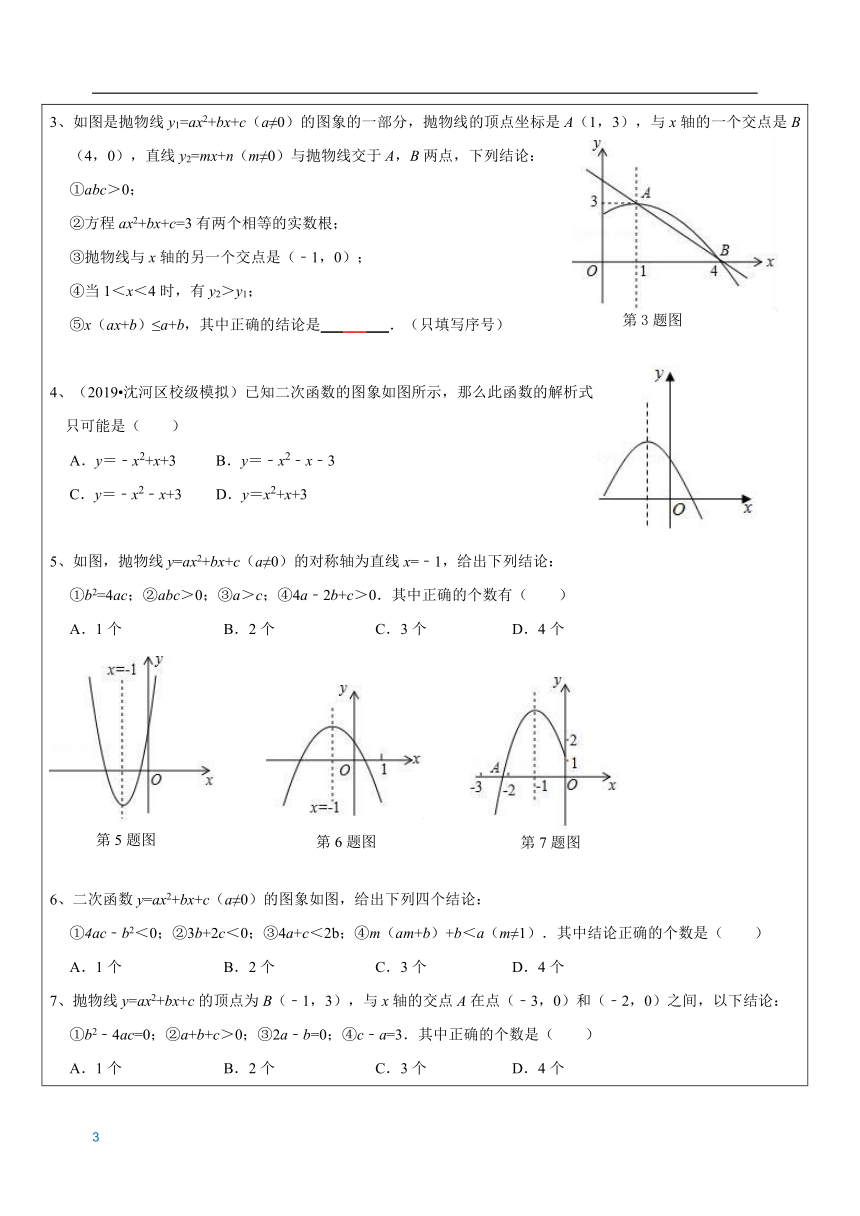
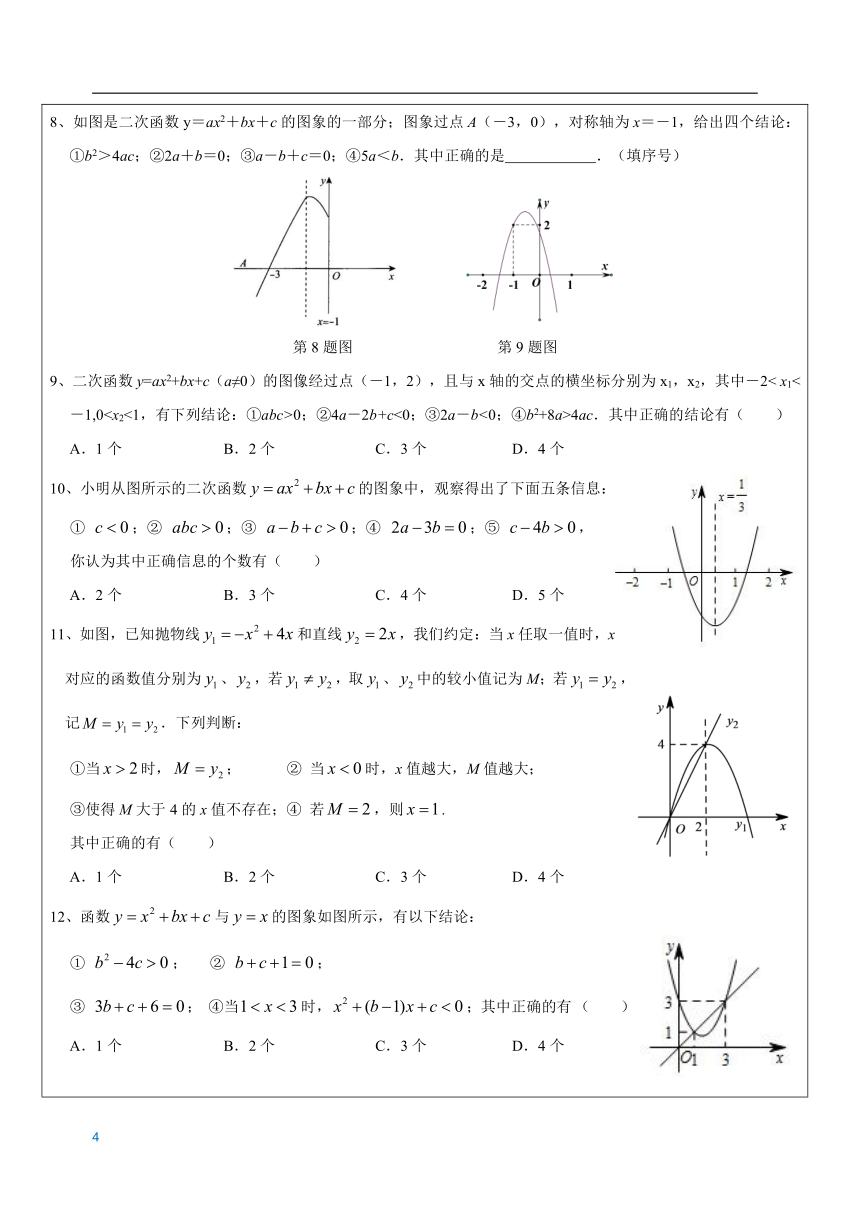
题型一：二次函数图像与系数的关系例1：图像共存问题1、（2019?新泰市二模）在同一平面直角坐标系中，一次函数y＝kx﹣2k和二次函数y＝﹣kx2+2x﹣4（k是常数且k≠0）的图象可能是（ ）A． B． C． D．2、（2018?李沧区校级自主招生）一次函数y＝cx+b与二次函数y＝ax2+bx+c在同一坐标系内的图象可能为（ ）A． B． C． D．3、（大庆模拟）在同一直角坐标系中，函数y＝ax+1与y＝ax2+bx+1（a≠0）的图象可能是（ ）A． B． C． D．4、已知a≠0，在同一直角坐标系中，函数y＝ax与y＝ax2的图象有可能是（ ）A． B． C． D．例2：图像与系数1、如图是二次函数的图象，下列结论：①；②；③.其中错误的个数是（ ） A．3 B．2 C．1 D．0 2、二次函数的图象如图所示，对称轴是直线，下列结论：①；②；③；④.其中正确的是（ ） A．①④ B．②④ C. ①②③ D．①②③④3、如图是抛物线y1=ax2+bx+c（a≠0）的图象的一部分，抛物线的顶点坐标是A（1，3），与x轴的一个交点是B（4，0），直线y2=mx+n（m≠0）与抛物线交于A，B两点，下列结论：①abc＞0；②方程ax2+bx+c=3有两个相等的实数根；③抛物线与x轴的另一个交点是（﹣1，0）；④当1＜x＜4时，有y2＞y1；⑤x（ax+b）≤a+b，其中正确的结论是 ．（只填写序号）4、（2019?沈河区校级模拟）已知二次函数的图象如图所示，那么此函数的解析式 只可能是（ ）A．y＝﹣x2+x+3 B．y＝﹣x2﹣x﹣3 C．y＝﹣x2﹣x+3 D．y＝x2+x+35、如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，给出下列结论：①b2=4ac；②abc＞0；③a＞c；④4a﹣2b+c＞0．其中正确的个数有（ ） A．1个 B．2个 C．3个 D．4个 6、二次函数y=ax2+bx+c（a≠0）的图象如图，给出下列四个结论：①4ac﹣b2＜0；②3b+2c＜0；③4a+c＜2b；④m（am+b）+b＜a（m≠1）．其中结论正确的个数是（ ） A．1个 B．2个 C．3个 D．4个 7、抛物线y=ax2+bx+c的顶点为B（﹣1，3），与x轴的交点A在点（﹣3，0）和（﹣2，0）之间，以下结论：①b2﹣4ac=0；②a+b+c＞0；③2a﹣b=0；④c﹣a=3．其中正确的个数是（ ） A．1个 B．2个 C．3个 D．4个8、如图是二次函数y＝ax2＋bx＋c的图象的一部分；图象过点A（－3，0），对称轴为x＝－1，给出四个结论：①b2＞4ac；②2a＋b＝0；③a－b＋c＝0；④5a＜b．其中正确的是 ．（填序号） 第8题图 第9题图 9、二次函数y=ax2+bx+c（a≠0）的图像经过点（－1，2），且与x轴的交点的横坐标分别为x1，x2，其中－2< x1<－1,00；②4a－2b+c<0；③2a－b<0；④b2+8a>4ac．其中正确的结论有（ ）A．1个 B．2个 C．3个 D．4个10、小明从图所示的二次函数的图象中，观察得出了下面五条信息：① ；② ；③ ；④ ；⑤ ， 你认为其中正确信息的个数有（ ）A．2个 B．3个 C．4个 D．5个11、如图，已知抛物线和直线，我们约定：当x任取一值时，x对应的函数值分别为、，若，取、中的较小值记为M；若，记．下列判断：①当时，； ② 当时，x值越大，M值越大；③使得M大于4的x值不存在；④ 若，则.其中正确的有（ ）A．1个 B．2个 C．3个 D．4个12、函数与的图象如图所示，有以下结论：① ； ② ；③ ； ④当时，；其中正确的有?（ ）A．1个 B．2个 C．3个 D．4个 题型二：求函数图像1、（2019?衢州）如图，正方形ABCD的边长为4，点E是AB的中点，点P从点E出发，沿E→A→D→C移动至终点C．设P点经过的路径长为x，△CPE的面积为y，则下列图象能大致反映y与x函数关系的是（ ）A． B． C． D．2、如图，在等腰△ABC中，AB=AC=4cm，∠B=30°，点P从点B出发，以cm/s的速度沿BC方向运动到点C停止，同时点Q从点B出发，以1cm/s的速度沿BA﹣AC方向运动到点C停止，若△BPQ的面积为y（cm2），运动时间为x（s），则下列最能反映y与x之间函数关系的图象是（ ）A． B． C． 3、如图，四边形ABCD为正方形，若AB=4，E是AD边上一点（点E与点A、D不重合），BE的中垂线交AB于M，交DC于N，设AE=x，则图中阴影部分的面积S与x的大致图象是（ ） A． B． C． D． 4、矩形ABCD中，BC=4，AB=2，P是线段BC边上一动点，Q在PC或其延长线上，且BP=PQ，以PQ为一边作正方形PQRS，若BP=x，正方形PQRS与矩形ABCD重叠部份的面积为y，则y与x的函数的大致图象是（ ） A． B． C． D． 5、四边形ABCD为直角梯形，CD∥AB，CB⊥AB且CD=BC=AB，若直线l⊥AB，直线l截这个梯形所得的位于此直线左方的图形面积为y，点A到直线L的距离为x，则y与x关系的大致图象为（ ） A． B． C． D． 6、如图，AB为半圆的直径，点P为AB上一动点，动点P从点A出发，沿AB匀速运动到点B，运动时间为t，分别以AP与PB为直径做半圆，则图中阴影部分的面积S与时间t之间的函数图象大致为（ ） A． B． C． D． 7、（2019?萧山区模拟）已知A，B两地相距120千米，甲、乙两人沿同一条公路从A地出发到B地，乙骑自行车，甲骑摩托车，图中DE，OC分别表示甲、乙离开A地的路程s（单位：千米）与时间t（单位：小时）的函数关系的图象，设在这个过程中，甲、乙两人相距y（单位：千米），则y关于t的函数图象是（ ）A． B． C． D．题型三：函数交点问题（数形结合）1、二次函数y=ax2+bx+c（a≠0）和正比例函数y=x的图象如图所示，则方程的两根之和（ ）A、大于0 B、等于0 C、小于0 D、不能确定2、已知，若使y=k成立的x值恰好有三个，则k的值为（?D ）A、0 B、?1 C、?2 D、?33、（2018秋?长兴县期末）超市有一种“喜之郎“果冻礼盒，内装两个上下倒置的果冻，果冻高为4cm，底面是个直径为6cm的圆，轴截面可以近似地看作一个抛物线，为了节省成本，包装应尽可能的小，这个包装盒的长AD（不计重合部分，两个果冻之间没有挤压）至少为（ ）A．（6+3）cm B．（6+2）cm C．（6+2）cm D．（6+3）cm4、设方程，试讨论k取不同范围的值时其不同解的个数的情况． 5、（2019?丰台区模拟）如图，排球运动员站在点O处练习发球，将球从O点正上方2m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x（m）满足关系式y＝a（x﹣k）2+h．已知球与O点的水平距离为6m时，达到最高2.6m，球网与O点的水平距离为9m．高度为2.43m，球场的边界距O点的水平距离为18m，则下列判断正确的是（ ）A．球不会过网 B．球会过球网但不会出界 C．球会过球网并会出界 D．无法确定6、（2019?宁波模拟）某民房发生火灾．两幢大楼的部分截面及相关数据如图，小明在甲楼A处透过窗户E发现乙楼F处出现火灾，此时A，E，F在同一直线上．跑到一楼时，消防员正在进行喷水灭火，水流路线呈抛物线，在1.2m高的D处喷出，水流正好经过E，F．若点B和点E、点C和点F的离地高度分别相同，现消防员将水流抛物线向上平移5m，再向左后退 m，恰好把水喷到F处进行灭火． 7、（顺义区一模）已知抛物线y＝﹣x2+2mx﹣m2+1与x轴交点为A、B（点B在点A的右侧），与y轴交于点C．（1）试用含m的代数式表示A、B两点的坐标；（2）当点B在原点的右侧，点C在原点的下方时，若△BOC是等腰三角形，求抛物线的解析式；（3）已知一次函数y＝kx+b，点P（n，0）是x轴上一个动点，在（2）的条件下，过点P作垂直于x轴的直线交这个一次函数的图象于点M，交抛物线y＝﹣x2+2mx﹣m2+1于点N，若只有当1＜n＜4时，点M位于点N的下方，求这个一次函数的解析式． 8、（门头沟区期末）已知关于x的方程mx2+（3m+1）x+3＝0（m≠0）．（1）求证：方程总有两个实数根；（2）若方程的两个实数根都是整数，求正整数m的值；（3）在（2）的条件下，将关于x的二次函数y＝mx2+（3m+1）x+3的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象．请结合这个新的图象回答：当直线y＝x+b与此图象有两个公共点时，b的取值范围． 9、（西城区二模）已知一次函数y1＝kx+b（k≠0）的图象经过（2，0），（4，1）两点，二次函数y2＝x2﹣2ax+4（其中a＞2）．（1）求一次函数的表达式及二次函数图象的顶点坐标（用含a的代数式表示）；（2）利用函数图象解决下列问题：①若a＝，求当y1＞0且y2≤0时，自变量x的取值范围；②如果满足y1＞0且y2≤0时的自变量x的取值范围内恰有一个整数，直接写出a的取值范围． 10、（朝阳区校级月考）已知二次函数y1＝x2+bx+c的图象C1经过（﹣1，0），（0，﹣3）两点．（1）求C1对应的函数表达式；（2）将C1先向左平移1个单位，再向上平移4个单位，得到抛物线C2，将C2对应的函数表达式记为y2＝x2+mx+n，求C2对应的函数表达式．（3）设y3＝2x+3，在（2）的条件下利用函数图象直接写出y2≤y3时x的取值范围．
第1题图
第2题图
第3题图
第7题图
第5题图
第6题图
D．
16
