人教版数学九年级上册 22.3 二次函数实际应用讲义(无答案)
文档属性
| 名称 | 人教版数学九年级上册 22.3 二次函数实际应用讲义(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 517.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-29 22:00:47 | ||
图片预览



文档简介
教师辅导讲义
学员编号: 年 级: 课 时 数: 学员姓名: 辅导科目: 学科教师:
授课类型 T同步(几何最值问题) C专题(抛物型问题) T能力(实际应用题)
授课日期及时段
教学内容
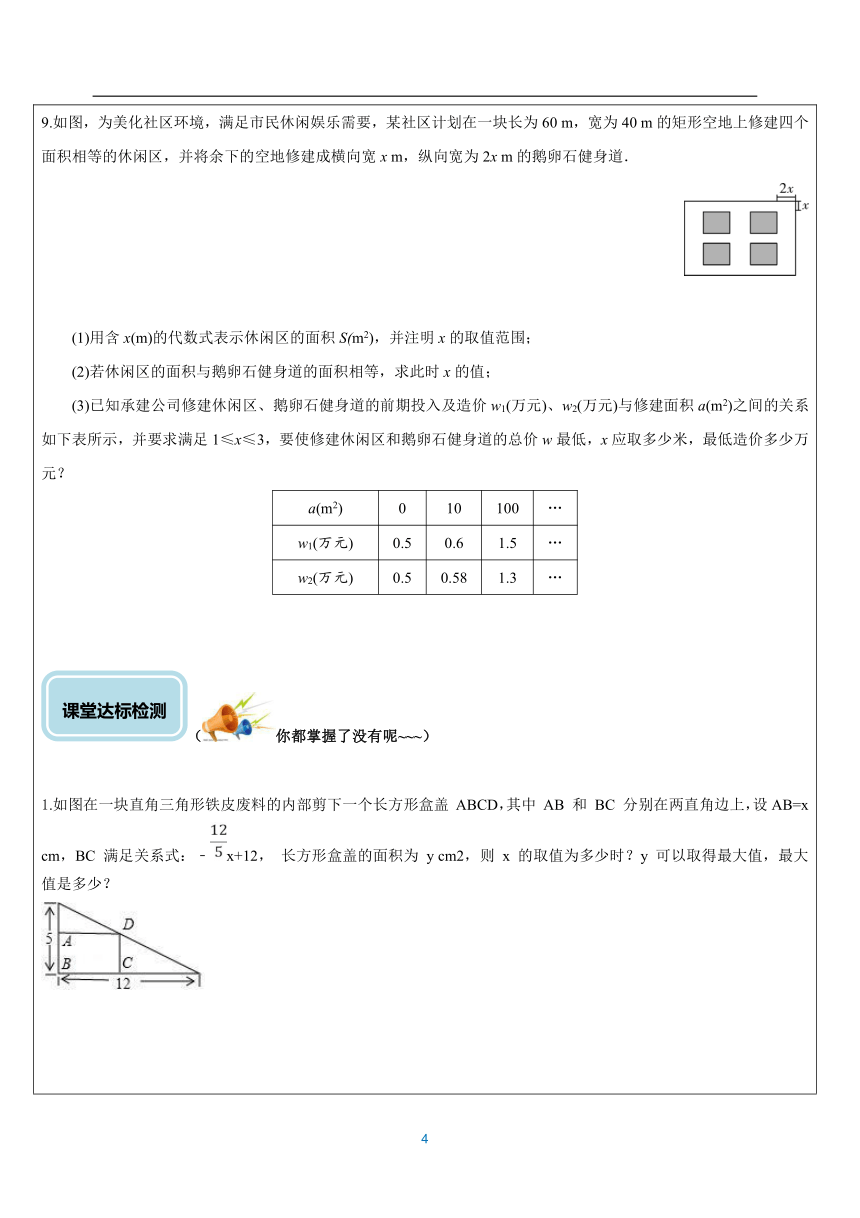
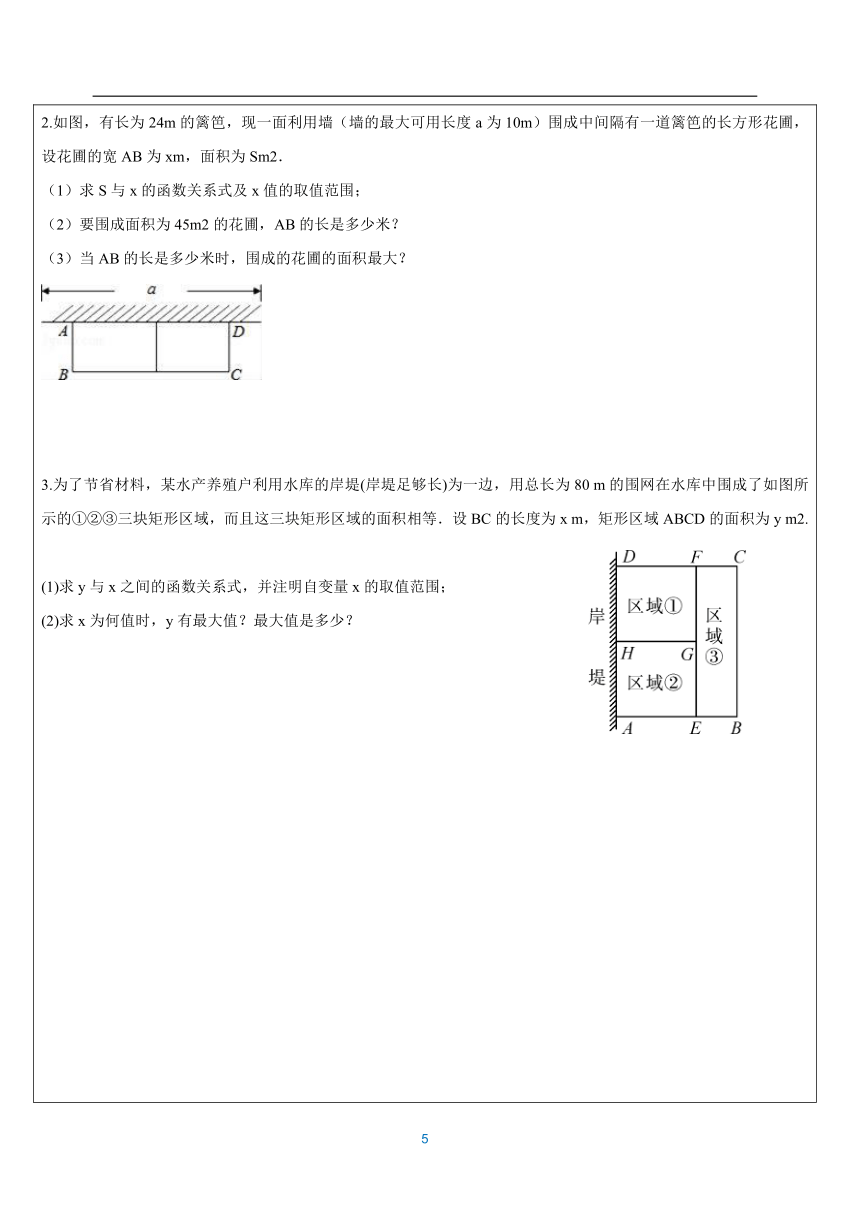
(大脑放电影~) 1.用长为12m的篱笆,一边利用足够长的墙围出一块苗圃。如图所示,围出的苗圃是五边形 ABCDE,AE⊥AB,BC⊥AB,∠C=∠D=∠E=120°,设CD=DE=x(m),五边形ABCDE的面积为S(m2).问:当x取什么值时,S最大?并求出S的最大值。2. 投资1万元围一个矩形菜园(如图),其中一边靠墙,另外三边选用不同材料建造.墙长24 m,平行于墙的边的费用为200元/m,垂直于墙的边的费用为150元/m,设平行于墙的边长为x m. (1)设垂直于墙的一边长为y m,直接写出y与x之间的函数关系式;(2)若菜园面积为384 m2,求x的值; (3)当x为何值时,菜园的面积最大,最大值为多少? 3.如图,有两面夹角为45°的墙体(∠ABC=45°).且墙AB= 米,墙BC=10米,小张利用8米长的篱笆围成了一个四边形菜园,如图,四边形BDEF,DE平行BC,∠E=90°(靠墙部分不使用篱笆),设EF=x,四边形面积为S.(1)用含x的代数式表示BD、DE的长; (2)求出S关于x的函数关系式,并写出x的取值范围; (3)求S的最大值. 4.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm. (1)若花园的面积为192m2,求x的值;(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值. 5.为了保护环境,实现城市绿化,某房地产公司要在拆迁的一块地上进行绿化改造,他们依据地势整理出了一块矩形区域ABCD,铺成人们可以活动的砖石地面,又分别以AB、BC、CD、DA为斜边向外作等腰直角三角形(如图所示),通过测量,发现四边形MNGH的周长正好为200米,设AB=x米,BC=y米 . (1)求y与x之间的函数关系式;(2)如果矩形区域ABCD 铺设砖石地面,建设费用为每平方米50元,其他区域种花草,建设费用为每平方米100元,设总建设费用为w元,求w与x之间的函数关系式;当x取何值时,w有最小值,最小值为多少? 6.国际慢城,闲静高淳,景区内有一块矩形油菜花田地(数据如图所示,单位:m),现在其中修建一条观花道(如图阴影所示),供游人赏花.设改造后剩余油菜花地所占面积为y m2.(1)求y与x的函数表达式; (2)若改造后观花道的面积为13 m2,求x的值; (3)若要求0.5≤x≤1,求改造后剩余油菜花地所占面积的最大值. 7.如图,工人师傅用一块长为10 dm,宽为6 dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形(厚度不计). (1)在图中画出裁剪示意图,用实线表示裁剪线、虚线表示折痕,并求长方体底面面积为12 dm2时,裁掉的正方形边长多大? (2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元.裁掉的正方形边长多大时,总费用最低,最低为多少? 8.王师傅承包了一片池塘养水产品,他用总长为88m的围网围成如图所示的5个区域,其中②③④⑤四个区域面积相等.设AH=xm,整个矩形区域的面积为ym2. (1)求y与x之间的函数关系式,并注明自变量x的取值范围; (2)当x为何值时,y取最大值?最大值是多少? 9.如图,为美化社区环境,满足市民休闲娱乐需要,某社区计划在一块长为60 m,宽为40 m的矩形空地上修建四个面积相等的休闲区,并将余下的空地修建成横向宽x m,纵向宽为2x m的鹅卵石健身道. (1)用含x(m)的代数式表示休闲区的面积S(m2),并注明x的取值范围; (2)若休闲区的面积与鹅卵石健身道的面积相等,求此时x的值; (3)已知承建公司修建休闲区、鹅卵石健身道的前期投入及造价w1(万元)、w2(万元)与修建面积a(m2)之间的关系如下表所示,并要求满足1≤x≤3,要使修建休闲区和鹅卵石健身道的总价w最低,x应取多少米,最低造价多少万元?a(m2) 0 10 100… w1(万元) 0.5 0.6 1.5… w2(万元) 0.5 0.58 1.3… (你都掌握了没有呢~~~) 1.如图在一块直角三角形铁皮废料的内部剪下一个长方形盒盖 ABCD,其中 AB 和 BC 分别在两直角边上,设AB=x cm,BC 满足关系式:﹣x+12, 长方形盒盖的面积为 y cm2,则 x 的取值为多少时?y 可以取得最大值,最大值是多少? 2.如图,有长为24m的篱笆,现一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm2. (1)求S与x的函数关系式及x值的取值范围; (2)要围成面积为45m2的花圃,AB的长是多少米? (3)当AB的长是多少米时,围成的花圃的面积最大?3.为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80 m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为x m,矩形区域ABCD的面积为y m2.(1)求y与x之间的函数关系式,并注明自变量x的取值范围;(2)求x为何值时,y有最大值?最大值是多少? (课堂精粹) 1.如图,一小球沿与地面成一定角度的方向飞出,小球的飞行路线是一条抛物线,如果不考虑空气阻力,小球的飞行高度y(单位:m)与飞行时间x(单位:s)之间具有函数关系y=-5x2+20x,请根据要求解答下列问题: (1)在飞行过程中,当小球的飞行高度为15 m时,飞行时间是多少? (2)在飞行过程中,小球从飞出到落地所用时间是多少?(3)在飞行过程中,小球飞行高度何时最大?最大高度是多少? 2.有一座抛物线拱型桥,在正常水位时,水面BC的宽为8米,拱桥的最高点D到水面BC的距离DO为4米,点O是BC的中点,如图,以点O为原点,直线BC为x轴,建立直角坐标系xOy. (1)求该抛物线的表达式; (2)如果水面BC上升3米(即OA=3)至水面EF,点E在点F的左侧,求水面宽度EF的长. 3.有一个抛物线型蔬菜大棚,将其截面放在如图所示的直角坐标系中,抛物线可以用函数y=ax2+bx来表示.已知大棚在地面上的宽度OA为10米,距离O点2米处的棚高BC为3米. (1)求该抛物线的函数关系式; (2)求蔬菜大棚离地面的最大高度是多少米? (3)若借助横梁DE建一个门,要求门的高度不低于1.5米,则横梁DE的宽度最多是多少米? 4.某校初三年级的一场篮球比赛中,如图,队员甲正在投篮,已知球出手时离地面 m,与篮圈中心的水平距离为7 m,当球出手后水平距离为4 m时到达最大高度4 m,篮圈距地面3 m,设篮球运行的轨迹为抛物线. (1)建立如图所示的平面直角坐标系,求此抛物线的解析式; (2)此球能否准确投中? (3)此时,若对方队员乙在甲前面1 m处跳起拦截,已知乙的最大摸高为3.1 m,那么他能否拦截成功? 5.如图,一个圆形喷水池的中央垂直于水面安装了一个柱形喷水装置OA,O恰好在水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,按如图所示建立直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式可以用y=-x2+bx+c表示,且抛物线经过点B(,),C(2,), 请根据以上信息,解答下列问题. (1)求抛物线的函数关系式,并确定喷水装置OA的高度; (2)喷出的水流距水面的最大高度是多少米? (3)若不计其他因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外? 6.某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点 A 处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上,在乒乓球运行时,设乒乓球与端点A 的水平距离为 x(米),与桌面的高度为 y(米),经多次测试后,得到如下部分数据: (1)由表中的数据及函数学习经验,求出 y 关于 x 的函数解析式; (2)试求出当乒乓球落在桌面时,其落点与端点 A 的水平距离是多少米? (3)当乒乓球落在桌面上弹起后,y与x之间满足 ①用含a的代数式表示k; ②已知球网高度为0.14米,球桌长(1.4×2)米.若a= -0.5,那么乒乓球弹起后,是否有机会在某个击球点可以将球沿直线扣杀到端点A? 请说明理由. ( 举一反三增能力! )1.平时我们在跳大绳时,绳甩到最高处的形状可近似地看为抛物线.如图所示,正在甩绳的甲、乙两名学生拿绳的手间距为,距地面均为,学生丙、丁分别站在距甲拿绳的手水平距离、处.绳子在甩到最高处时刚好通过他们的头顶.已知学生丙的身高是,则学生丁的身高为(建立的平面直角坐标系如图所示)( ) A. 1.5m B. 1.625m C. 1.66m D. 1.67m 2.如图,图中是抛物线形拱桥,当拱顶离水面2m时水面宽4m.水面下降1m,水面宽度为( ) A. 2m B. 2m C. m D. m 3.如图,桥洞的拱形是抛物线,其顶部C离水面的距离为3,水面宽为AB.以水平向右方向为x轴的正方向,建立平面直角坐标系.①当点C为原点时,抛物线解析式是y=﹣x2,若选取点B为坐标原点,则抛物线解析式为_____. 4.甲、乙两人进行羽毛球比赛,甲发出一个十分关键的球,出手点为,羽毛球距地面高度(米)与其飞行的水平距离(米)之间的关系式为.如图,已知球网距原点米,乙(用线段表示)扣球的最大高度为米,设乙的起跳点的横坐标为,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则的取值范围是( ) A. . B. C. D. 5.如图所示,一位运动员在离篮下米水平距离处起跳投篮,球运行的路线是抛物线,当球运行的水平距离是米时,球达到最大高度米.已知篮筐中心到地面的距离为米,问球出手时离地面________米时才能投中. 6.两幢大楼的部分截面及相关数据如图,小明在甲楼A处透过窗户E发现乙楼F处出现火灾,此时A,E,F在同一直线上.跑到一楼时,消防员正在进行喷水灭火,水流路线呈抛物线,在1.2m高的D处喷出,水流正好经过E,F. 若点B和点E、点C和F的离地高度分别相同,现消防员将水流抛物线向上平移0.4m,再向左后退了____m,恰好把水喷到F处进行灭火.7.某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,
喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在水
池中心的装饰物处汇合,如图所示,以水平方向为x轴,喷水池中心为原点建立直角坐标系. ? (1)求水柱所在抛物线(第一象限部分)的函数表达式; (2)王师傅在水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内? (3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后水柱的最大高度. (化腐朽为神奇) 1.新春佳节,电子鞭炮因其安全、无污染开始走俏.某商店经销一种电子鞭炮,已知这种电子鞭炮的成本价为每盒80元,市场调查发现,该种电子鞭炮每天的销售量y(盒)与销售单价x(元)有如下关系:y=-2x+320(80≤x≤160).设这种电子鞭炮每天的销售利润为w元. (1)求w与x之间的函数关系式; (2)该种电子鞭炮销售单价定为多少元时,每天的销售利润最大?最大利润是多少元? 2.某旅行社推出一条成本价为500元/人的省内旅游线路,游客人数y(人/月)与旅游报价x(元/人)之间的关系为y=-x+1300,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间. (1)要将该旅游线路每月游客人数控制在200人以内,求该旅游线路报价的取值范围; (2)求经营这条旅游线路每月所需要的最低成本; (3)当这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少? 3.某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件. (1)求商场经营该商品原来一天可获利润多少元? (2)设后来该商品每件降价x元,商场一天可获利润y元.①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?②求出y与x之间的函数关系式,并直接写出当x取何值时,商场可获得最大利润,最大利润为多少元? 4.某公司2017年初刚成立时投资1000万元购买新生产线生产新产品,此外,生产每件该产品还需要成本40元.按规定,该产品售价不得低于60元/件且不得超过160元/件,且每年售价确定以后不再变化,该产品销售量y(万件)与产品售价x(元)之间的函数关系如图所示. (1)求y与x之间的函数关系式,并写出x的取值范围; (2)求2017年该公司的最大利润? (3)在2017年取得最大利润的前提下,2018年公司将重新确定产品售价,能否使两年共盈利达980万元,若能,求出2018年产品的售价;若不能,请说明理由. 5.某公司生产一种产品,每件成本为2元,售价为3元,年销售量为100万件.为获取更好的效益,公司准备拿出一定资金做广告,通过市场调查发现:每年投入的广告费用为x(单位:十万元) 时,产品的年销售量将是原来的y倍,同时y又是x的二次函数,且满足的相互关系如下表:x 0 1 2… y 1 1.5 1.8… (1)求y与x之间的函数关系式; (2)如果把利润看作是销售总额减去成本费和广告费,试写出年利润s(单位:十万元)与广告费x(单位:十万元)的函数关系; (3)如果公司一年投入的年广告费为10-30万元,问广告费在什么范围内,公司获得的年利润随广告费的增大而增加?公司可获得的最大年利润是多少? 6.每年5月的第二个星期日即为母亲节,“父母恩深重,恩怜无歇时”,许多市民喜欢在母亲节为母亲送鲜花,感恩母亲,祝福母亲.节日前夕,某花店采购了一批鲜花礼盒,成本价为每件30元,分析上一年母亲节的鲜花礼盒销售情况,得到了如下数据,同时发现每天的销售量y(件)是销售单价x(元/件)的一次函数. 销售单价x (元/件)… 30 40 50 60… 每天销售 量y (件)… 350 300 250 200… (1)求出y与x的函数关系; (2)物价局要求,销售该鲜花礼盒获得的利润不得高于100%.①当销售单价x取何值时,该花店销售鲜花礼盒每天获得的利润为5000元?(利润=销售总价-成本总价);②试确定销售单价x取何值时,花店销售该鲜花礼盒每天获得的利润W(元)最大?并求出花店销售该鲜花礼盒每天获得的最大利润. 7.某种商品的成本为每件20元,经市场调查发现,这种商品在未来40天内的日销售量m(件)与x(天)的关系如表. 时间x(天) 1 3 6 10 36… 日销售量m(件) 94 90 84 76 24… 未来40天内,前20天每天的价格y1(元/件)与时间x(天)的函数关系式为y1=x+25(1≤x≤20且x为整数),后20天每天的价格y2(元/件)与时间x(天)的函数关系式为y2=-x+40(21≤x≤40且x为整数). (1)求日销售量m(件)与时间x(天)之间的关系式; (2)请预测本地市场在未来40天中哪一天的日销售利润最大?最大日销售利润是多少? 8.某蔬菜基地种植西红柿,由历年市场行情得知,从2月1日起的300天内,西红柿市场售价与上市时间的关系用图(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图(2)的抛物线段Q=(t﹣150)2+100 (0≤t≤300)表示,(注:市场售价和种植成本的单位:元/100kg,时间单位:天)(1)写出图(1)表示的市场售价P与时间t的函数关系式;(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大? (真金不怕火炼) 1.某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为: 若企业销售该产品获得的利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函 数解析式; (2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少? (3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围。 2.某养殖户长期承包一口鱼塘养鱼,每年养一批,从鱼苗放入养成到成品需要300天,鱼塘承包费用每年5000元,他记录了前几年平均每天投入饲养量(单位:kg)与年底成品鱼(达到一定规格可以销售)产量之间的关系如下表:
平均每天投入饲料(kg)2025304050607080 成品鱼产量(kg)28003000320036003900400039003600 (1)请用适当的函数模型描述平均每天投入饲料数量与成品产量之间的关系; (2)如果今年的饲料价格为1.6元/kg,成品鱼销售价为20元/kg,鱼苗费用4000元.假设养成的成品鱼全部都能按此价格卖出,请建立适当的函数模型分析:平均每天投入饲料多少千克时,该养殖户当年在该鱼塘养殖场这种鱼获得的利润最多,最多利润是多少元?(利润=销售收入-饲料成本-鱼塘承包费-鱼苗成本). 3.我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如下表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示. 时间t(天) 0 5 10 15 20 25 30 日销售量 y1(百件) 0 25 40 45 40 25 0 (1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映y1与t的变化规律,并求出y与t的函数关系式及自变量t的取值范围; (2)求y2与t的函数关系式,并写出自变量t的取值范围; (3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为y(百件),求y与t的函数关系式;当t为何值时,日销售总量y达到最大,并求出此时的最大值. 4.某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完,该公司的年产量为6千件,若在国内市场销售,平均每件产品的利润y1(元)与国内销售数量x(千件)的关系为:[来源:Zxxk.Com] HYPERLINK "http://www.zzstep.com" \o "中国教育出版网\" 若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为:[ww#w.zzs^tep.~*com%][www.z%#z&ste*@p.com] (1) 用x的代数式表示t为:t= ;当0<x≤4时,y2与x的函数关系为y2= ;当4≤x< 时,y2=100; (2)求每年该公司销售这种健身产品的总利润w(千元)与国内的销售数量x(千件)的函数关系式,并指出x的取值范围; (3)该公司每年国内、国外的销售量各为多少时,可使公司每年的总利润最大?最大值为多少? 5.某药厂销售部门根据市场调研结果,对该厂生产的一种新型原料药未来两年的销售进行预测,井建立如下模型:设第t个月该原料药的月销售量为P(单位:吨),P与t之间存在如图所示的函数关系,其图象是函数P=(0<t≤8)的图象与线段AB的组合;设第t个月销售该原料药每吨的毛利润为Q(单位:万元),Q与t之间满足如下关系:Q=(1)当8<t≤24时,求P关于t的函数解析式;(2)设第t个月销售该原料药的月毛利润为w(单位:万元)①求w关于t的函数解析式;②该药厂销售部门分析认为,336≤w≤513是最有利于该原料药可持续生产和销售的月毛利润范围,求此范围所对应的月销售量P的最小值和最大值.
T同步——二次函数与几何
几何面积最大值问题
课堂达标检测
C专题——抛物线型
专题导入
强化练习
T能力——实际应用题
针对培养
分段函数
1
同课章节目录
