人教版数学九年级上册 第二十二章 二次函数存在性问题讲义(无答案)
文档属性
| 名称 | 人教版数学九年级上册 第二十二章 二次函数存在性问题讲义(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 484.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-29 23:34:12 | ||
图片预览



文档简介
教师辅导讲义
学员编号: 年 级: 课 时 数: 学员姓名: 辅导科目: 学科教师:
授课类型 C专题( 二次函数存在性问题 )
授课日期及时段
教学内容
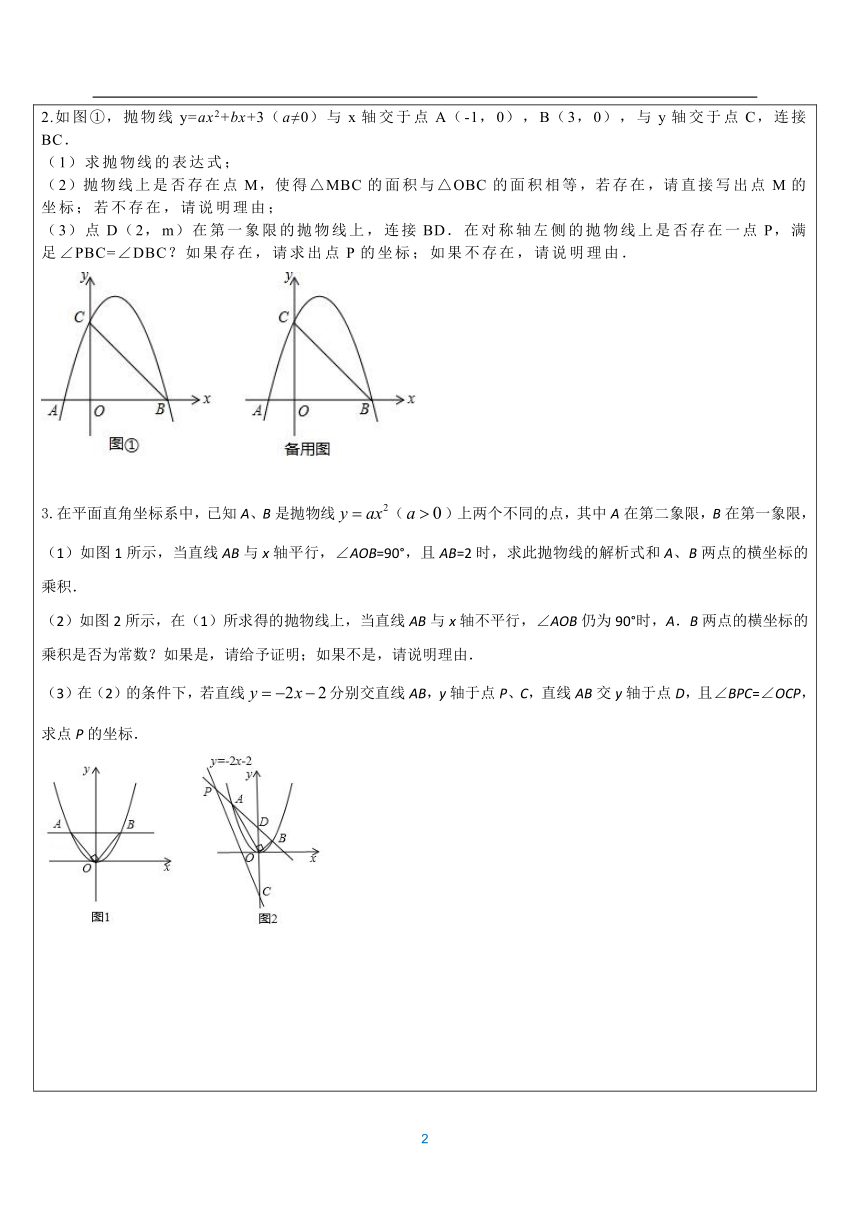
角的存在性问题1.抛物线与x轴交于点A,B(A在B的左侧),与y轴交于点C. (1)求直线BC的解析式; (2)抛物线的对称轴上存在点P,使∠APB=∠ABC,利用图1求点P的坐标; (3)点Q在y轴右侧的抛物线上,利用图2比较∠OCQ与∠OCA的大小,并说明理由. 2.如图①,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(-1,0),B(3,0),与y轴交于点C,连接BC.
(1)求抛物线的表达式;
(2)抛物线上是否存在点M,使得△MBC的面积与△OBC的面积相等,若存在,请直接写出点M的坐标;若不存在,请说明理由;
(3)点D(2,m)在第一象限的抛物线上,连接BD.在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P的坐标;如果不存在,请说明理由.
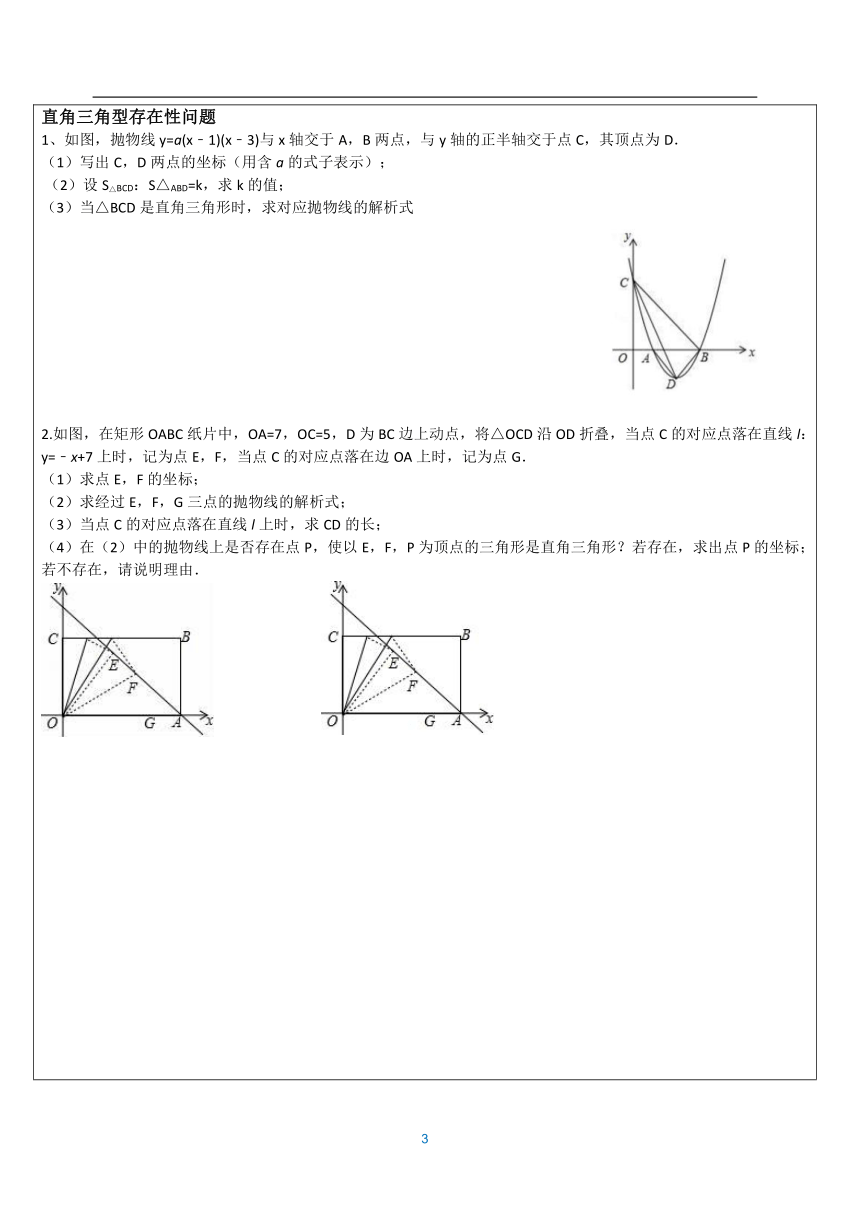
3.在平面直角坐标系中,已知A、B是抛物线()上两个不同的点,其中A在第二象限,B在第一象限,(1)如图1所示,当直线AB与x轴平行,∠AOB=90°,且AB=2时,求此抛物线的解析式和A、B两点的横坐标的乘积.(2)如图2所示,在(1)所求得的抛物线上,当直线AB与x轴不平行,∠AOB仍为90°时,A.B两点的横坐标的乘积是否为常数?如果是,请给予证明;如果不是,请说明理由.(3)在(2)的条件下,若直线分别交直线AB,y轴于点P、C,直线AB交y轴于点D,且∠BPC=∠OCP,求点P的坐标. 直角三角型存在性问题1、如图,抛物线y=a(x﹣1)(x﹣3)与x轴交于A,B两点,与y轴的正半轴交于点C,其顶点为D.? 写出C,D两点的坐标(用含a的式子表示); ?(2)设S△BCD:S△ABD=k,求k的值;?(3)当△BCD是直角三角形时,求对应抛物线的解析式 2.如图,在矩形OABC纸片中,OA=7,OC=5,D为BC边上动点,将△OCD沿OD折叠,当点C的对应点落在直线l:y=﹣x+7上时,记为点E,F,当点C的对应点落在边OA上时,记为点G. (1)求点E,F的坐标; (2)求经过E,F,G三点的抛物线的解析式; (3)当点C的对应点落在直线l上时,求CD的长; (4)在(2)中的抛物线上是否存在点P,使以E,F,P为顶点的三角形是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由. 3.如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ACB=90°,抛物线经过A,B两点,其中点A,C的坐标分别为(1,0),(﹣4,0),抛物线的顶点为点D.(1)求抛物线的解析式;(2)点E是直角三角形ABC斜边AB上的一个动点(不与A,B重合),过点E作x轴的垂线,交抛物线于点F,当线段FE的长度最大时,求点E的坐标;(3)在(2)的条件下,抛物线上是否存在一点P,使△PEF是以EF为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.4.如图,抛物线y=ax2+2x与x轴相交于点B,其对称轴为x=3.(1)求直线AB的解析式;(2)过点O作直线l,使l∥AB,点P是l上一动点,设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为t,当0<S≤18时,求t的取值范围;(3)在(2)的条件下,当t取最大值时,抛物线上是否存在点Q,使△OPQ为直角三角形且OP为直角边,若存在,求出点Q的坐标;若不存在,说明理由. 等腰三角形存在性问题1.如图,已知抛物线y=的图象与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C. (1)求直线BC的解析式; (2)点F是直线BC下方抛物线上的一点,当△BCF的面积最大时,在抛物线的对称轴上找一点P,使得△BFP的周长最小,请求出点F的坐标和点P的坐标; (3)在(2)的条件下,是否存在这样的点Q(0,m),使得△BFQ为等腰三角形?如果有,请直接写出点Q的坐标;如果没有,请说明理由. 2.如图,在平面直角坐标系中,抛物线与轴交于、两点,交轴于点,点关于抛物线对称轴的对称点为点. (1)求线段的长度; (2)为线段上方抛物线上的任意一点,点为,一动点从点出发运动到轴上的点,再沿轴运动到点.当四边形的面积最大时,求的最小值; (3)将线段沿轴向右平移,设平移后的线段为,直至平行于轴(点为第2小问中符合题意的点),连接直线.将绕着旋转,设旋转后、的对应点分别为、,在旋转过程中直线与轴交于点,与线段交于点.当是以为腰的等腰三角形时,写出的长度. 等腰直角三角形存在性问题1.如图①,已知抛物线y=ax+bx+c的图象经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m. (1)求抛物线的解析式; (2)若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值; (3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由。2.如图,已知抛物线y=ax+bx+c(a≠0)与x轴交于点A(1,0)和点B(?3,0),与y轴交于点C,且OC=OB. (1)求此抛物线的解析式; (2)若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求出此时点E的坐标; (3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90?后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标。 平行四形存在性问题 1.如图,已知抛物线y=与x轴交于点A,B,点A的坐标为(-1,0),与y轴交于点C(0,2),点D与点C关于x轴对称,点P是x轴正半轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q,交直线BD于点M. (1)求该抛物线所表示的二次函数的表达式; (2)若m=3,试证明△BQM是直角三角形; (3)已知点F(0,),试求m为何值时,四边形DMQF是平行四边形? 2.如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.(1)求点E坐标及经过O,D,C三点的抛物线的解析式; (2)一动点P从点C出发,沿CB以每秒2个单位长的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长的速度向点C运动,当点P到达点B时,两点同时停止运动.设运动时间为t秒,当t为何值时,DP=DQ;(3)若点N在(2)中的抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使得以M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点的坐标;若不存在,请说明理由. 菱形存在性问题 1.在直角坐标系xOy中,已知点P是反比例函数y=(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A. (1)如图1,当⊙P运动到与x轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由; (2)如图2,当⊙P运动到与x轴相交,设交点为点B、C.当四边形ABCP是菱形时,求出点A、B、C的坐标 (3)在(2)的条件下,求出经过A、B、C三点的抛物线的解析式. 9、如图,抛物线与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6. ⑴求抛物线的解析式及点D的坐标;? ⑵连接BD,F为抛物线上一动点,当∠FAB=∠EDB时,求点F的坐标;?⑶平行于x轴的直线交抛物线于M,N两点,以线段MN为对角线作菱形MPNQ,当点P在x轴上,且时,求菱形对角线MN的长. 矩形存在性问题 1.如图所示,在平面直角坐标系xOy中,抛物线(a<0)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.? (1)求A,B两点的坐标及抛物线的对称轴;? (2)求直线l的函数表达式(其中k、b用含a的式子表示);? (3)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为,求a的值;?(4)设P是抛物线的对称轴上的一点,点Q在抛物线,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由. 2.如图,抛物线y=﹣x2+bx+c和直线y=x+1交于A,B两点,点A在x轴上,点B在直线x=3上,直线x=3与x轴交于点C(1)求抛物线的解析式;(2)点P从点A出发,以每秒个单位长度的速度沿线段AB向点B运动,点Q从点C出发,以每秒2个单位长度的速度沿线段CA向点A运动,点P,Q同时出发,当其中一点到达终点时,另一个点也随之停止运动,设运动时间为t秒(t>0).以PQ为边作矩形PQNM,使点N在直线x=3上.①当t为何值时,矩形PQNM的面积最小?并求出最小面积;②直接写出当t为何值时,恰好有矩形PQNM的顶点落在抛物线上. 正方形存在性问题1.如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).? (1)请直接写出B、C两点的坐标及抛物线的解析式;? (2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE=∠OCD? ?(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,请求出t的值.
C专题——二次函数存在性问题
存在性问题
1
同课章节目录
