人教版数学九年级上册23.1图形的旋转讲义(无答案)
文档属性
| 名称 | 人教版数学九年级上册23.1图形的旋转讲义(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 692.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-29 23:33:54 | ||
图片预览


文档简介
教师辅导讲义
学员编号: 年 级: 课 时 数: 学员姓名: 辅导科目: 学科教师:
授课类型 T同步( 图形的旋转 ) C专题( 旋转作图 )
授课日期及时段
教学内容
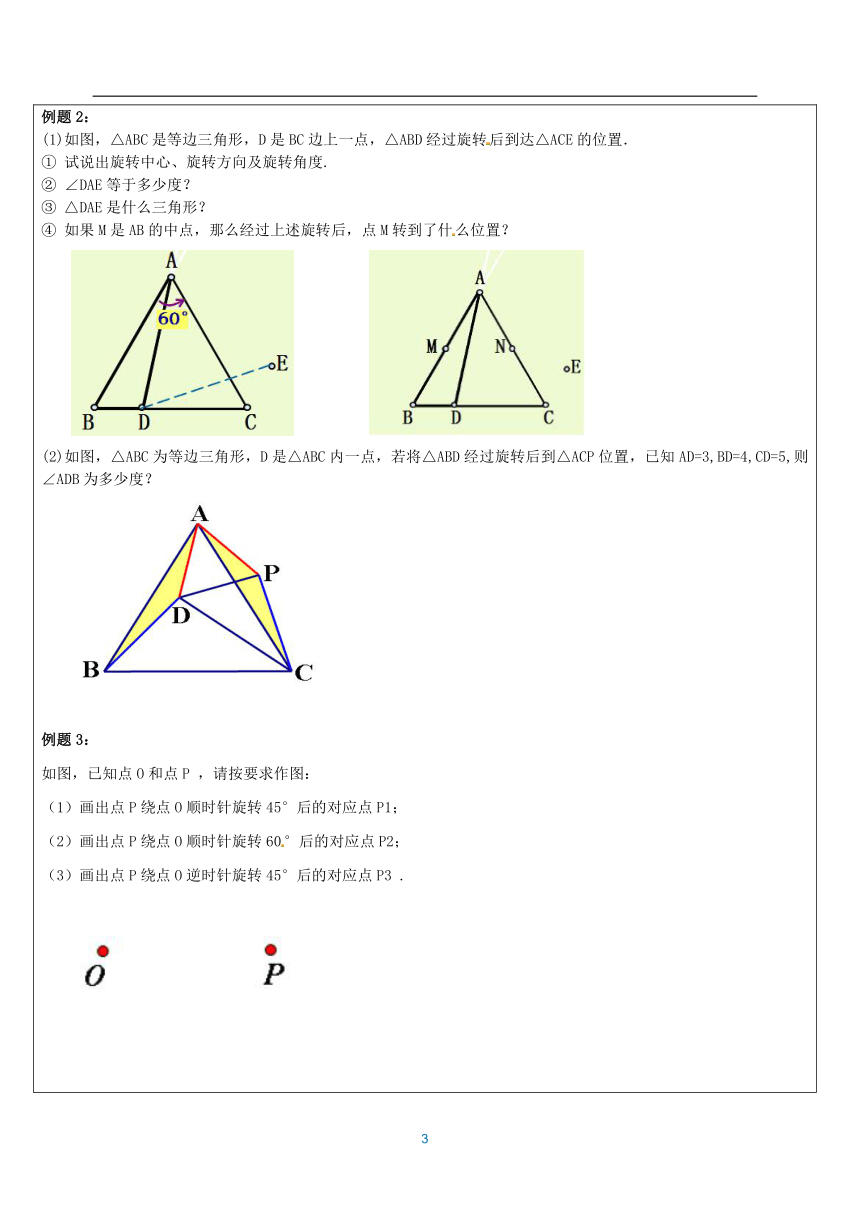
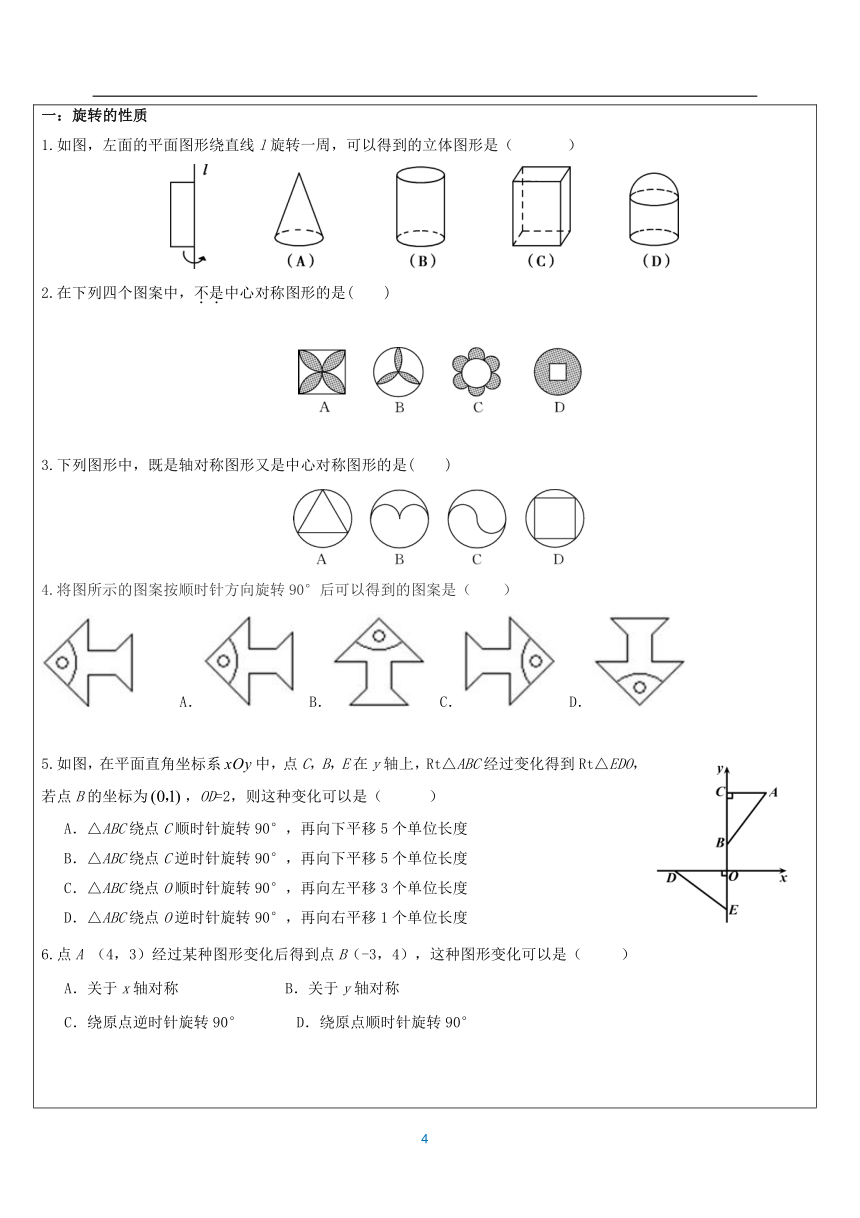
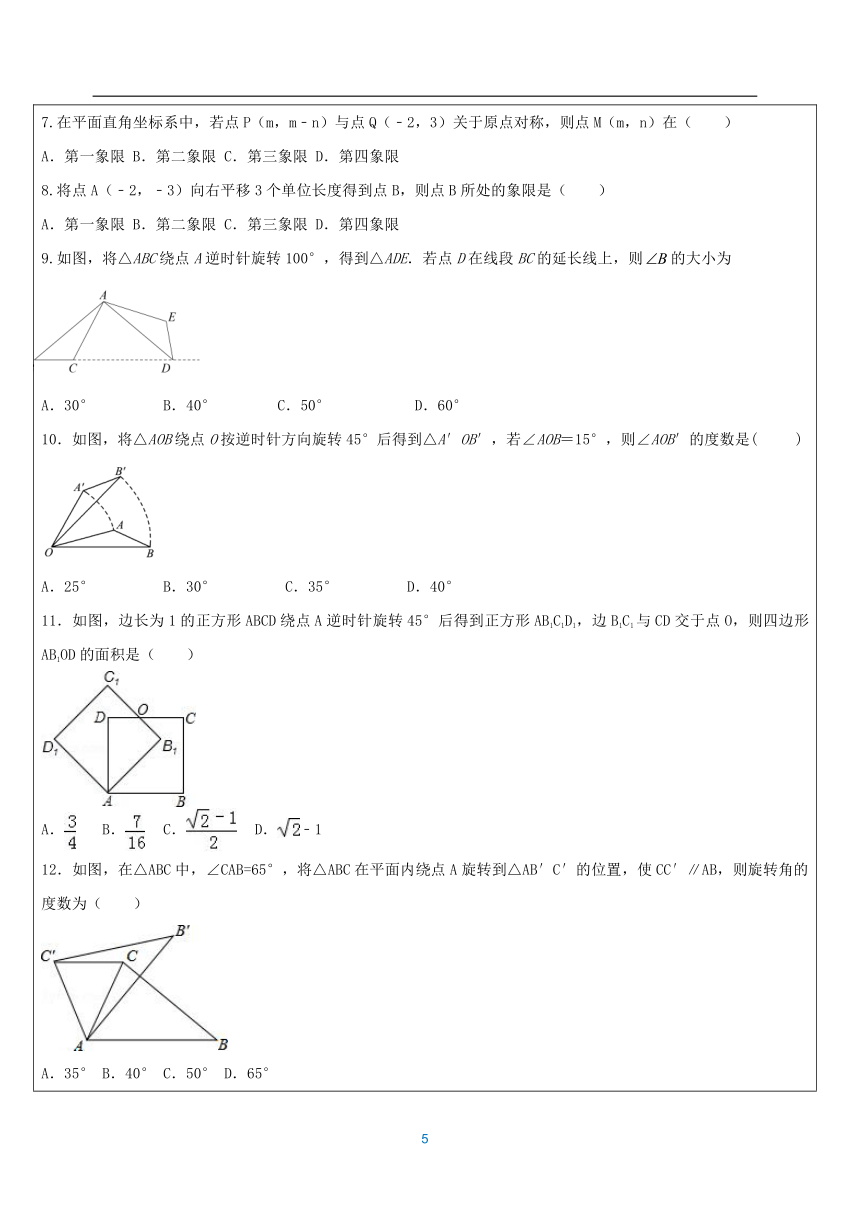
(大脑放电影~) 知识点1:旋转定义在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。 图形的旋转是图形上的每一点在平面上绕着某个固定点旋转固定角度的位置移动,其中对应点到旋转中心的距离相等,对应线段的长度、对应角的大小相等,旋转前后图形的大小和形状没有改变。知识点2:图形旋转性质(1)对应点到旋转中心的距离相等。 (2)对应点与旋转中心所连线段的夹角等于旋转角。知识点3:旋转对称中心把一个图形绕着一个点旋转一定的角度后,与原来的图形相吻合,这种图形叫做 旋转对称图形,这个定点叫做 旋转对称中心,旋转的角度叫做 旋转角。(旋转角大于0°小于360°) (热个身先~~~) 旋转的有关概念:把一个图形绕着某一点转动一个角度的图形变换叫做旋转,点叫做__________,转动的角叫做__________,如果图形上的点经过旋转变为点,那么这两个点叫做这个旋转的__________.(如图) 注意:⑴研究旋转问题应把握三个元素:__________与__________、__________. ⑵每一组对应点所构成的旋转角__________. 例1:如图,把四边形AOBC绕点O旋转得到四边形DOEF. 在这个旋转过程中: (1)旋转中心是谁? (2)旋转方向如何? (3)经过旋转,点A、B的对应点分别是谁? (4)图中哪个角是旋转角? (5)四边形AOBC与四边形DOEF的形状、大小有何关系? (6) AO与DO的长度有什么关系? BO与EO呢? (7)∠AOD与∠BOE的大小有什么关系? 例题2: (1)如图,△ABC是等边三角形,D是BC边上一点,△ABD经过旋转后到达△ACE的位置. ① 试说出旋转中心、旋转方向及旋转角度. ② ∠DAE等于多少度? ③ △DAE是什么三角形? ④ 如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置? (2)如图,△ABC为等边三角形,D是△ABC内一点,若将△ABD经过旋转后到△ACP位置,已知AD=3,BD=4,CD=5,则∠ADB为多少度?例题3: 如图,已知点O和点P ,请按要求作图: (1)画出点P绕点O顺时针旋转45°后的对应点P1; (2)画出点P绕点O顺时针旋转60°后的对应点P2; (3)画出点P绕点O逆时针旋转45°后的对应点P3 . 一:旋转的性质1.如图,左面的平面图形绕直线l旋转一周,可以得到的立体图形是( )2.在下列四个图案中,不是中心对称图形的是( ) 3.下列图形中,既是轴对称图形又是中心对称图形的是( )4.将图所示的图案按顺时针方向旋转90°后可以得到的图案是( ) A. B. C. D. 5.如图,在平面直角坐标系中,点C,B,E在y轴上,Rt△ABC经过变化得到Rt△EDO,若点B的坐标为,OD=2,则这种变化可以是( ) A.△ABC绕点C顺时针旋转90°,再向下平移5个单位长度 B.△ABC绕点C逆时针旋转90°,再向下平移5个单位长度 C.△ABC绕点O顺时针旋转90°,再向左平移3个单位长度 D.△ABC绕点O逆时针旋转90°,再向右平移1个单位长度6.点A (4,3)经过某种图形变化后得到点B(-3,4),这种图形变化可以是( )A.关于x轴对称 B.关于y轴对称 C.绕原点逆时针旋转90° D.绕原点顺时针旋转90° 7.在平面直角坐标系中,若点P(m,m﹣n)与点Q(﹣2,3)关于原点对称,则点M(m,n)在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限8.将点A(﹣2,﹣3)向右平移3个单位长度得到点B,则点B所处的象限是( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限9.如图,将△ABC绕点A逆时针旋转100°,得到△ADE.若点D在线段BC的延长线上,则的大小为 A.30° B.40° C.50° D.60°10.如图,将△AOB绕点O按逆时针方向旋转45°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是( )A.25° B.30° C.35° D.40°11.如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( ) A. B. C. D.﹣1 12.如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( ) A.35° B.40° C.50° D.65°13.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( ) A.48 B.96 C.84 D.4214.如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到的△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的大小是( ) A.32° B.64° C.77° D.87°15.如图,将△ABC绕点C顺时针旋转得到△DEC,使点A的对应点D恰好落在边AB上,点B的对应点为E,连接BE,下列结论一定正确的是( ) A.AC=AD B.AB⊥EB C.BC=DE D.∠A=∠EBC16.如图,四边形ABCD是边长为5的正方形,E是DC上一点,DE=1,将△ADE绕着点A顺时针旋转到与△ABF重合,则EF=( )A. B. C. D.17.如图,等边三角形OAD的顶点A(2,0),延长OD至点C,使CD=AD,以AD,CD为邻边作菱形ABCD;延长CB交x轴于点A1,延长DC至点C1,使CC1=CA1,以A1C,CC1为邻边作菱形A1B1C1C;以此类推,依次得到菱形A2B2C2C1,菱形A3B3C3C2…菱形AnBnCnCn-1.则菱形AnBnCnCn-1的面积为( ) B. C. D.18.如图,已知?ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的大小为( ) A.130° B.150° C.160° D.170°19.如图,E、F分别是正方形ABCD的边AB、BC上的点,且BE=CF,连接CE、DF,将△DCF绕着正方形的中心O按顺时针方向旋转到△CBE的位置,则旋转角为( ) A.30° B.45° C.60° D.90° 20.如图,将△ABC绕顶点C逆时针旋转得到△A′B′C′,且点B刚好落在A′B′上,若∠A=25°,∠BCA′=45°,则∠A′BA等于( ) A.30° B.35° C.40° D.45°21.某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( ) A.甲种方案所用铁丝最长 B.乙种方案所用铁丝最长 C.丙种方案所用铁丝最长 D.三种方案所用铁丝一样长22.如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( ) A.4,30° B.2,60° C.1,30° D.3,60°23.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为( )30 , 2 B. 60 ,2 C.60 , D. 60 ,
1.在圆、平行四边形、矩形、菱形、正方形、等腰三角形等图形中,是中心对称图形但不是轴对称图形的是__________________.2.如图,C是线段BD上一点,分别以BC,CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于点F,BE交AC于点G,则图中可通过旋转而相互得到的三角形是: __________________________________________________________________(要求把符合条件的都写出来).
3.如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为______度.
4.如图,在平面直角坐标系中,点的坐标为,等腰直角三角形的边在轴的正半轴上,,点在点的右侧,点在第一象限。将绕点逆时针旋转,如果点的对应点恰好落在轴的正半轴上,那么边的长为__________. 5.如图,在平面直角坐标系xOy中,点A,点B的坐标分别为(,), (,),将线段AB沿x轴的正方向平移,若点B的对应点的坐标为(,),则点A的对应点的坐标为 . 分别以正方形的各边为直径向其内部作半圆得到的图形如图所示.将该图形绕其中心旋转一个合适的角度后会与原图形重合,则这个旋转角的最小度数是______度. 7.在平面直角坐标系中,点绕坐标原点顺时针旋转后,恰好落在右图中阴影区域(包括边界)内,则的取值范围是 .8.如图,在Rt△ABC中,∠ABC=90°,AB=BC=,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .9.如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=3,则BE= . 10.如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF= .11.若点(a,1)与(﹣2,b)关于原点对称,则ab= .12.如图,在平面直角坐标系中,△DEF可以看作是△ABC经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△ABC得到△DEF的过程: .13.如图,在平面直角坐标系中,点,分别在轴、 轴上, . 先将线段沿轴翻折得到线段,再将线段绕点顺时针旋转30°得到线段,连接. 若点的坐标为 ,则线段的长为 . 14.如图,在平面直角坐标系xOy中,正方形OABC的边长为1,点D,E分别在OA,OC上,OD = CE,△OCD可以看作是△CBE经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△CBE得到△OCD的过程: .15.如图,△ABC为等边三角形,P为三角形内一点,将△ABP绕A点逆时针旋转60°后与△ACP′重合,若AP=3,则PP′=______.
16.如图,将△ABC绕点A按逆时针方向旋转得到△ADE,DE交AC于F,交BC于G,若∠C=35°,∠EFC=60°,则这次旋转了______°.
17.如图,把△ABC绕点C顺时针旋转25°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A=______.
18.如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为,则AK= .(课堂精粹) 1.如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D. (1)求证:BE=CF; (2)当四边形ACDE为菱形时,求BD的长. 2.如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置. (1)旋转中心是点 ,旋转角度是 度; (2)若连结EF,则△AEF是 三角形;并证明; (3)若四边形AECF的面积为25,DE=2,求AE的长. 3.在平面直角坐标系xOy中,已知A(﹣1,5),B(4,2),C(﹣1,0)三点. (1)点A关于原点O的对称点A′的坐标为 ,点B关于x轴的对称点B′的坐标为 ,点C关于y轴的对称点C的坐标为 . (2)求(1)中的△A′B′C′的面积. 4.如图所示,在网格中建立了平面直角坐标系,每个小正方形的边长均为1个单位长度,将四边形ABCD绕坐标原点O按顺时针方向旋转180°后得到四边形A1B1C1D1.
(1)直接写出D1点的坐标;
(2)将四边形A1B1C1D1平移,得到四边形A2B2C2D2,若D2(4,5),画出平移后的图形.(友情提示:画图时请不要涂错阴影的位置哦!)
5.如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3). (1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标; (2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2; (3)求出(2)中C点旋转到C2点所经过的路径长(记过保留根号和π).6.如图,△ABC各顶点的坐标分别是A(﹣2,﹣4),B(0,﹣4),C(1,﹣1). (1)在图中画出△ABC向左平移3个单位后的△A1B1C1; (2)在图中画出△ABC绕原点O逆时针旋转90°后的△A2B2C2; (3)在(2)的条件下,AC边扫过的面积是 .7.如图,已知△ABC三个顶点坐标分别是A(1,3),B(4,1),C(4,4). (1)请按要求画图: ①画出△ABC向左平移5个单位长度后得到的△A1B1C1; ②画出△ABC绕着原点O顺时针旋转90°后得到的△A2B2C2. (2)请写出直线B1C1与直线B2C2的交点坐标.8.如图,已知正方形OABC在直角坐标系xOy中,点A、C分别在x轴、y轴的正半轴上,点O在坐标原点.等腰直角三角板OEF的直角顶点O在原点,E、F分别在OA、OC上,且OA=4,OE=2.将三角板OEF绕O点逆时针旋转至OE1F1的位置,连接CF1、AE1.
(1)求证:△OAE1≌△OCF1;
(2)若三角板OEF绕O点逆时针旋转一周,是否存在某一位置,使得OE∥CF?若存在,请求出此时E点坐标;若不存在,请说明理由. 9.已知△ACB为等腰直角三角形,∠ACB=90°,点E在AC上,EF⊥AC交AB于F,连BE、CF、M、N分别为CF、BE的中点.
(1)如图1,则=_____________,并说明理由;
(2)如图2,将△AEF绕点A顺时针旋转45゜,(1)中的结论是否成立?并加以证明.
T同步——同步训练
同步知识梳理
同步题型分析
C专题
专题导入
1
同课章节目录
