2.1.3 相等向量与共线向量 课件 28张PPT
文档属性
| 名称 | 2.1.3 相等向量与共线向量 课件 28张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 09:03:14 | ||
图片预览






文档简介
(共28张PPT)
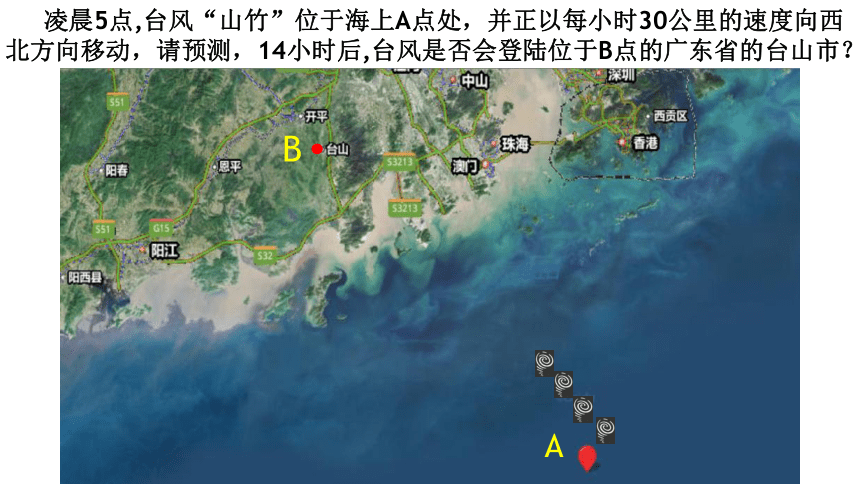
凌晨5点,台风“山竹”位于海上A点处,并正以每小时30公里的速度向西
北方向移动,请预测,14小时后,台风是否会登陆位于B点的广东省的台山市?
数 量
只有大小,没有方向
单位1;数0
加、减、乘、除等
数量的应用
数量的学习内容
二、向量表示
一、向量的定义:
既有大小又有方向的量.
一、向量的定义:
二、向量表示
1.有向线段
定义:带有方向的线段叫做有向线段.
表示:
长度:线段 的长度也叫做有向线段
的长度,记作 .
三要素:起点、方向、长度.
既有大小又有方向的量.
2.向量的几何表示:可以用有向
线段表示.
3.向量的代数表示:用表示有向
线段的起点和终点字母表示 ;
也可以用字母 , , 表示.
二 、向量表示
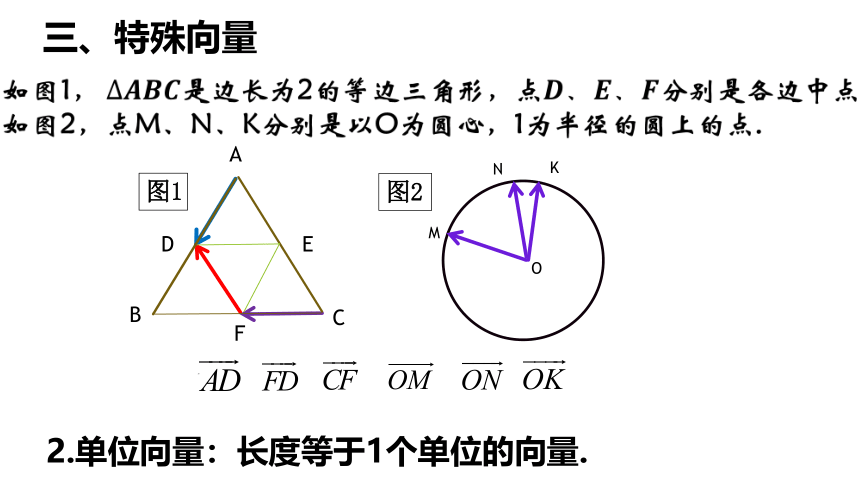
三、特殊向量
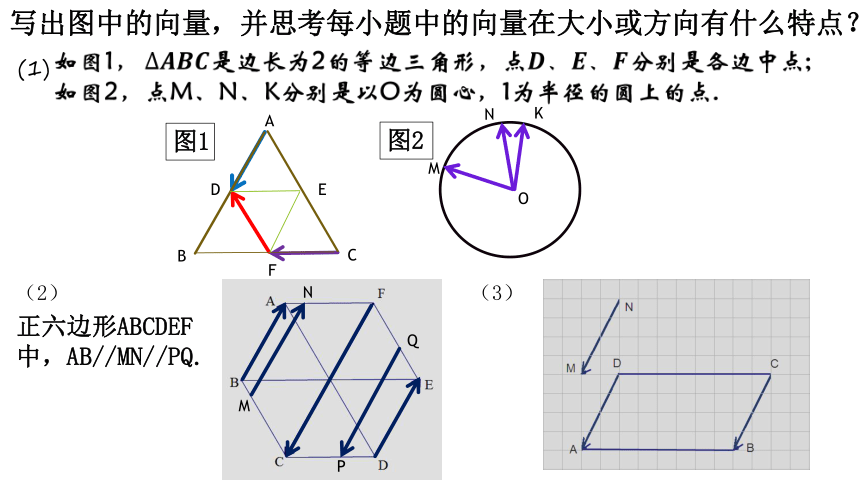
写出图中的向量,并思考每小题中的向量在大小或方向有什么特点?
(1)
(2)
(3)
正六边形ABCDEF
中,AB//MN//PQ.
图1
图2
三、特殊向量
2.单位向量:长度等于1个单位的向量.
图1
图2
3.平行向量:方向相同或相反的非零
向量叫做平行向量。记作: ;
例1.判断下面结论是否正确.
×
三、特殊向量
M
N
Q
P
√
例2.判断下列结论是否正确.
×
√
√
三、特殊向量
(3)
5.共线向量:任一组平行向量都可以
移动到同一条直线上,因此,
平行向量也叫做共线向量.
例3.判断如下结论是否正确.
共线向量一定在同一条直线上。 ( )
×
三、特殊向量
课堂练习:下列结论中正确的有:
(3)若两向量平行,则这两个向量
的方向相同或相反。
(2)
例2.判断下列结论是否正确.
×
√
×
×
×
×
×
√
√
三、特殊向量
零向量:长度为0的向量.
单位向量:长度等于1个单位的向量.
相等向量:长度相等且方向相同的向量叫做相等向量. 记作
平行向量:方向相同或相反的非零向量叫做平行向量。记作: ;
我们规定:零向量与任一向量平行,即对任意向量 ,都有 .
共线向量:任一组平行向量都可以移动到同一条直线上,因此,
平行向量也叫做共线向量.
四、向量之间的关系
在此处添加第一个项目要点
在此处添加第二个项目要点
在此处添加第三个项目要点
在此处添加第一个项目要点
在此处添加第二个项目要点
在此处添加第三个项目要点
标题和包含图表的内容布局
包含表格的两栏内容布局
此处是第一个项目要点
此处是第二个项目要点
此处是第三个项目要点
组 1 组 2
类 1 82 95
类 2 76 88
类 3 84 90
标题和包含 SmartArt 的内容布局
带题注布局的图片
题注
凌晨5点,台风“山竹”位于海上A点处,并正以每小时30公里的速度向西
北方向移动,请预测,14小时后,台风是否会登陆位于B点的广东省的台山市?
数 量
只有大小,没有方向
单位1;数0
加、减、乘、除等
数量的应用
数量的学习内容
二、向量表示
一、向量的定义:
既有大小又有方向的量.
一、向量的定义:
二、向量表示
1.有向线段
定义:带有方向的线段叫做有向线段.
表示:
长度:线段 的长度也叫做有向线段
的长度,记作 .
三要素:起点、方向、长度.
既有大小又有方向的量.
2.向量的几何表示:可以用有向
线段表示.
3.向量的代数表示:用表示有向
线段的起点和终点字母表示 ;
也可以用字母 , , 表示.
二 、向量表示
三、特殊向量
写出图中的向量,并思考每小题中的向量在大小或方向有什么特点?
(1)
(2)
(3)
正六边形ABCDEF
中,AB//MN//PQ.
图1
图2
三、特殊向量
2.单位向量:长度等于1个单位的向量.
图1
图2
3.平行向量:方向相同或相反的非零
向量叫做平行向量。记作: ;
例1.判断下面结论是否正确.
×
三、特殊向量
M
N
Q
P
√
例2.判断下列结论是否正确.
×
√
√
三、特殊向量
(3)
5.共线向量:任一组平行向量都可以
移动到同一条直线上,因此,
平行向量也叫做共线向量.
例3.判断如下结论是否正确.
共线向量一定在同一条直线上。 ( )
×
三、特殊向量
课堂练习:下列结论中正确的有:
(3)若两向量平行,则这两个向量
的方向相同或相反。
(2)
例2.判断下列结论是否正确.
×
√
×
×
×
×
×
√
√
三、特殊向量
零向量:长度为0的向量.
单位向量:长度等于1个单位的向量.
相等向量:长度相等且方向相同的向量叫做相等向量. 记作
平行向量:方向相同或相反的非零向量叫做平行向量。记作: ;
我们规定:零向量与任一向量平行,即对任意向量 ,都有 .
共线向量:任一组平行向量都可以移动到同一条直线上,因此,
平行向量也叫做共线向量.
四、向量之间的关系
在此处添加第一个项目要点
在此处添加第二个项目要点
在此处添加第三个项目要点
在此处添加第一个项目要点
在此处添加第二个项目要点
在此处添加第三个项目要点
标题和包含图表的内容布局
包含表格的两栏内容布局
此处是第一个项目要点
此处是第二个项目要点
此处是第三个项目要点
组 1 组 2
类 1 82 95
类 2 76 88
类 3 84 90
标题和包含 SmartArt 的内容布局
带题注布局的图片
题注
