高中数学人教新课标A版必修5第一章解三角形阅读与思考 海伦和秦九韶 课件 19张PPT
文档属性
| 名称 | 高中数学人教新课标A版必修5第一章解三角形阅读与思考 海伦和秦九韶 课件 19张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 10:41:38 | ||
图片预览




文档简介
(共19张PPT)
人教A版高中数学必修五
阅读与思考——
师者 所以传道、授业、解惑也
培能
以及数学史的渗透
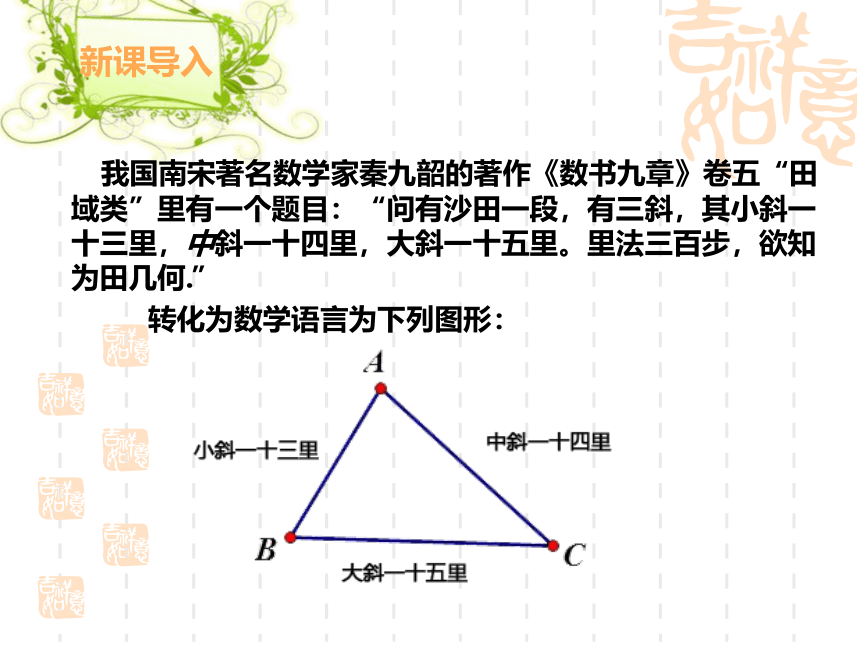
我国南宋著名数学家秦九韶的著作《数书九章》卷五“田域类”里有一个题目:“问有沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里。里法三百步,欲知为田几何.”
转化为数学语言为下列图形:
新课导入
知识回顾
3.余弦定理中我们得到三个推论:(从三角形三边计算出三角形三个角)
1.初中学过的三角形面积公式:
我国南宋著名数学家秦九韶的著作《数书九章》卷五“田域类”里有一个题目:“问有沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里。里法三百步,欲知为田几何.”
转化为数学语言为下列图形:
新课导入
新课导入
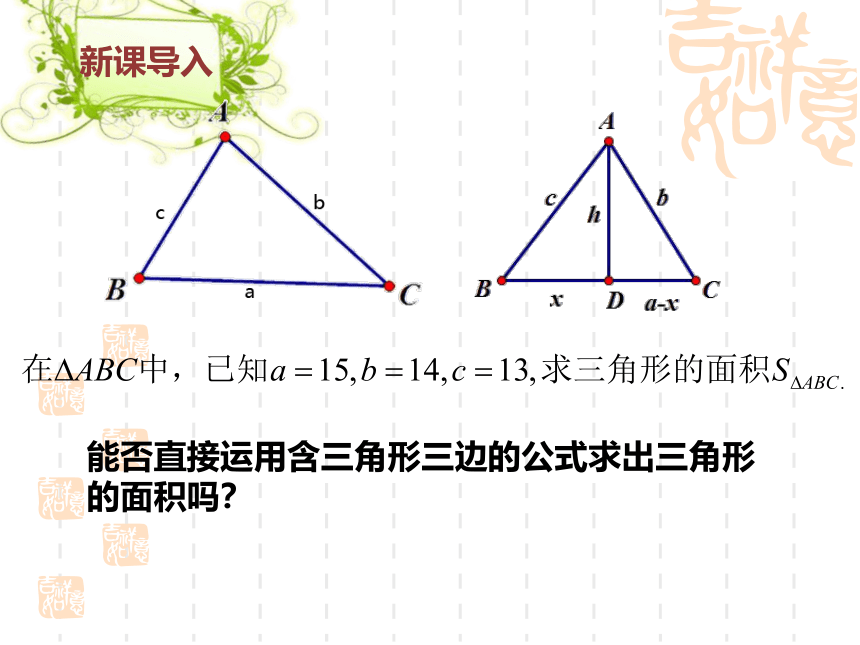
能否直接运用含三角形三边的公式求出三角形的面积吗?
新知探究
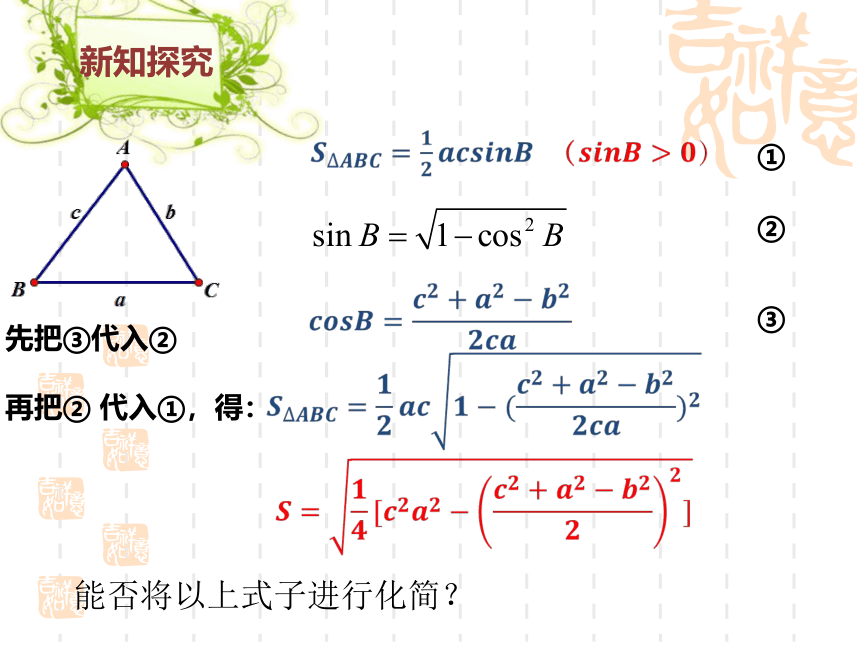
①
②
③
先把③代入②
再把② 代入①,得:
能否将以上式子进行化简?
新知探究
新知探究
新知探究
得出公式
海伦公式
秦九韶的
“三斜求积”公式
等价
“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实。一为从偶,开平方得积。”
人物简介
海伦(heron)
海伦(Heron),(10年----75年)古希腊的数学家、测量学家和机械学家。他的代表作是《度量术》,此书讨论平面图形的面积、立体图形的体积以及把图形分成比例部分。其中最著名的是已知三边长求三角形面积的海伦公式。
《测量仪器》是他的另一本代表作,其中描述的一种仪器,功能相当于现代的经纬仪。在此书中他还讨论许多测量的问题,如怎样挖隧道,从山的两侧开始,找准方向,使隧道准确会合;确定两点间的高度;测量可望不可及的两点之间的距离;还有还有各种高度和距离的测量问题。
人物简介
秦九韶
秦九韶(1202-1261年),字道古,汉族,生于普州安岳(今四川省安岳县),祖籍鲁郡(今河南范县)。 南宋官员、数学家,与李冶、杨辉、朱世杰并称宋元数学四大家。精研星象、音律、算术、诗词、弓剑、营造之学。
人物简介
秦九韶
他的《数书九章》概括了宋元时期中国传统数学的主要成就,尤其是系统总结和发展了高次方程的数值解法与一次同余问题的解法,提出了相当完备的“正负开方术”和“大衍求一术”,对数学发展产生了广泛的影响。秦九韶是一位既重视理论又重视实践,既善于继承又勇于创新的数学家,他被国外科学史家称为是“他那个民族,那个时代,并且确实也是所有时代最伟大的数学家之一”。
公式应用
课堂练习
课堂小结
余弦定理
“三斜求积”公式
海伦公式
等价
作 业
1.在△ABC中,角A,B,C,所对边分别为a,b,c,若a=7cm,b=3cm,c=8cm,则△ABC的面积是多少?
3.在△ABC中,角A,B,C,所对边分别为a,b,c,若a=15,b=8,c=17,则△ABC的面积是多少?
愿同学们在今后地学习和生活中,善于继承和发扬,勇于探索,追求卓越!
人教A版高中数学必修五
阅读与思考——
师者 所以传道、授业、解惑也
培能
以及数学史的渗透
我国南宋著名数学家秦九韶的著作《数书九章》卷五“田域类”里有一个题目:“问有沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里。里法三百步,欲知为田几何.”
转化为数学语言为下列图形:
新课导入
知识回顾
3.余弦定理中我们得到三个推论:(从三角形三边计算出三角形三个角)
1.初中学过的三角形面积公式:
我国南宋著名数学家秦九韶的著作《数书九章》卷五“田域类”里有一个题目:“问有沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里。里法三百步,欲知为田几何.”
转化为数学语言为下列图形:
新课导入
新课导入
能否直接运用含三角形三边的公式求出三角形的面积吗?
新知探究
①
②
③
先把③代入②
再把② 代入①,得:
能否将以上式子进行化简?
新知探究
新知探究
新知探究
得出公式
海伦公式
秦九韶的
“三斜求积”公式
等价
“以小斜幂并大斜幂减中斜幂,余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实。一为从偶,开平方得积。”
人物简介
海伦(heron)
海伦(Heron),(10年----75年)古希腊的数学家、测量学家和机械学家。他的代表作是《度量术》,此书讨论平面图形的面积、立体图形的体积以及把图形分成比例部分。其中最著名的是已知三边长求三角形面积的海伦公式。
《测量仪器》是他的另一本代表作,其中描述的一种仪器,功能相当于现代的经纬仪。在此书中他还讨论许多测量的问题,如怎样挖隧道,从山的两侧开始,找准方向,使隧道准确会合;确定两点间的高度;测量可望不可及的两点之间的距离;还有还有各种高度和距离的测量问题。
人物简介
秦九韶
秦九韶(1202-1261年),字道古,汉族,生于普州安岳(今四川省安岳县),祖籍鲁郡(今河南范县)。 南宋官员、数学家,与李冶、杨辉、朱世杰并称宋元数学四大家。精研星象、音律、算术、诗词、弓剑、营造之学。
人物简介
秦九韶
他的《数书九章》概括了宋元时期中国传统数学的主要成就,尤其是系统总结和发展了高次方程的数值解法与一次同余问题的解法,提出了相当完备的“正负开方术”和“大衍求一术”,对数学发展产生了广泛的影响。秦九韶是一位既重视理论又重视实践,既善于继承又勇于创新的数学家,他被国外科学史家称为是“他那个民族,那个时代,并且确实也是所有时代最伟大的数学家之一”。
公式应用
课堂练习
课堂小结
余弦定理
“三斜求积”公式
海伦公式
等价
作 业
1.在△ABC中,角A,B,C,所对边分别为a,b,c,若a=7cm,b=3cm,c=8cm,则△ABC的面积是多少?
3.在△ABC中,角A,B,C,所对边分别为a,b,c,若a=15,b=8,c=17,则△ABC的面积是多少?
愿同学们在今后地学习和生活中,善于继承和发扬,勇于探索,追求卓越!
