高中数学人教新课标A版必修5第一章解三角形阅读与思考 海伦和秦九韶 课件 20张PPT
文档属性
| 名称 | 高中数学人教新课标A版必修5第一章解三角形阅读与思考 海伦和秦九韶 课件 20张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 265.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
1.2 应用举例—海伦与秦九韶公式
一.阅读引领,师生探究.
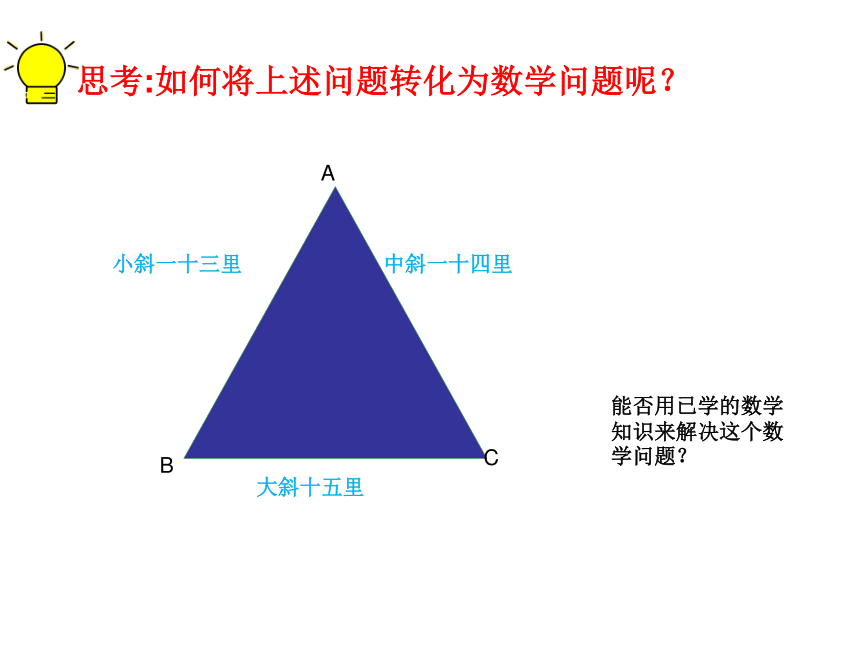
我国南宋著名数学家秦九韶(约1202—1261),在他的著作《算数九章》卷五“田域类 ”里有这样一个题目:
“问有沙田一段,有三斜.其小斜一十三里,中斜一十四里,
大斜一十五里.里法三百步.欲知几何.”意思是已知一个三
角形的三边长分别为13里,14里,15里,则这个沙田的
面积为多少?
思考:如何将上述问题转化为数学问题呢?
A
小斜一十三里
中斜一十四里
B
C
大斜十五里
能否用已学的数学知识来解决这个数学问题?
A
c
b
B
C
a
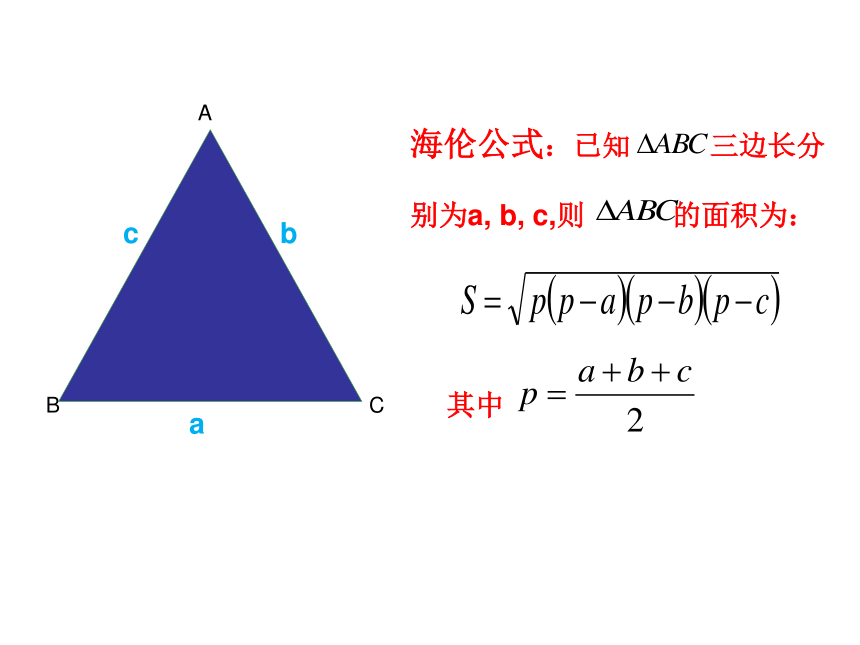
海伦公式:已知 三边长分
别为a, b, c,则 的面积为:
其中
海伦的生平
海伦(Heron),古希腊数学家.生
卒于亚历山大城.他擅长测量,给出
了多种求图形面积和体积的定理和公
式,最著名的是已知三边长求三角形
面积的海伦公式.海伦有许多学术著
.主要著作有《量度论》,《体积求法》,《几何》等.
????
二.古希腊数学
古希腊的数学发展到亚历山大里亚时期,数学的应用性得 到了很大的发展,其突出的一点就是三角术的发展.三角术是人们为了建立定量的天文学,以便用来预报天体的运行路线和位置以帮助报时,计算日历、航海和研究地理而产生的.
在解三角形问题中.一个比较困难的问题是如何由三角形的三边a, b, c,直接求出三角形的面积.据说这个问题最早是由古希腊数学家阿基米德解决的,他得到了公式:
但现在人们常常以古希腊的数学家海伦命名这个公式,称此公式为海伦公式,因为这个公式最早出现在海伦的著作《测地术》中,并在海伦的著作《测量仪器》和《度量术》中给出证明,海伦公式的特点是形式很美,大家很容易记住公式.
,其中
思考:通过你对古希腊数学文化的了解,对于已知三角形三边求三角形面积的数学问题你是否有一定的启发?
三、学习中国文化,增强民族自信心
我国南宋著名数学家秦九韶(约1202—1261)在他的著作《算
数九章》也提到了与海伦公式等价的从三角形的三边求面积的公
式,他把这种方法称为“三斜求积”,《算数九章》中的求法是:
“以小斜幂并大斜幂减中斜幂,余半之,自乘于上.以小斜幂乘大
斜幂减上,余四约之,为实.一为从隅,开平方的积.”如果把以上
这段文字写成公式,就是:
三斜求积公式与公元1世纪古希腊数学家海伦给出的公式殊途
同归,他虽然与海伦公式形式上不一样,但两者完全等价.它填
补了我国传统数学的空白,从中可以充分说明我国古代已具有
很高的数学水平.
思考:怎样证明这两个公式相等?
,其中
秦九韶生平
秦九韶,字道古.鲁郡(今河南范县)人. 中国古代
数学家.南宋嘉定元年(1208年)生;约景定(1261
年)年被贬至梅州,咸淳四年(1268)二月,在梅州辞
世,时年61岁.
《算数九章》 全书九章十八卷,九章九类:“大衍类”、
“天时类”、“田域类”、“测望类”、“赋役类”、“钱谷类”、
“营建类”、“军旅类”、“市物类”,每类9题(9问)共计
81题(81问),该书内容丰富至极,上至天文、星象、
历律、测候,下至河道、水利、建筑、运输,尤其是系统总结和发展了高次方程的数值
解法与一次同余问题的解法,提出了相当完备.”正负开方术”和”大衍求一术”对数学发展
产生了广泛的影响.
大衍求一术
秦九韶的“大衍求一术”,被康托尔称为“最幸运的天才”.秦九韶所发明的“大衍求一术”,即现代数中一次同余式组解法,是中世纪世界数学的成就之一,比西方1801年著名数学家高斯(Gauss,1777—1855年)建立的同余理论早554年,被西方称为“中国剩余定理”
正负开方术
秦九韶在《数书九章》中除“大衍求一术”外,还创拟了正负开方术,即任意高次方程的数值解法,秦九韶所发明的此项成果比1819年英国人霍纳(W·G·Horner,1786—1837年)的同样解法早572年.
秦九韶的成就也代表了中世纪世界数学发展的主流与最高水平,在世界数学史上占有崇高的地位.
四、合作探究
,其中
古希腊数学家海伦运用平面知识,证明海伦面积公式.中国古代数学家秦九韶
只给出公式,用来解决已知三角形三边求三角形面积这类问题的计算.
你能通过已学知识给出秦九韶面积公式的证明吗?
证明:如图,在△ABC中,过A作高AD交BC于D,
设 ,那 么 .
由于AD是△ABD、△ACD的公共边.
五、应用举
南宋时期的数学家秦九韶独立发现的计算三角形面积的“三斜求积
术”,与著名的海伦公式等价,其求法是:“以小斜幂并大斜幂减中斜幂,
余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实.一为从隅,
开平方得积.”若把以上这段文字写成公式,
若 的周长为
用“三斜求积术”求 面积=________;
[针对训练]中国宋代的数学家秦九韶曾提出“三斜求积术”,即假设在平面内有
一个三角形,边长分别为a,b,c.三角形的面积可由公式
求得,其中p为三角形周长的一半,这个公式也被称为海伦-秦九韶公式,现有一个三
角形的边长满足 则此三角形面积的最大值=_________.
六、师生小结
,其中
<2>秦九韶:南宋著名数学家,代表作《算数九章》''三斜求积术“已知
三边长求三角形面积
<1>海伦(Heron):古希腊数学家主要著作有《量度论》,《体积求法》,《几何》
等,最著名的是已知三边长求三角形面积的海伦公式.
七、知识拓展与提升
若将海伦公式推广到四边形,即设四边形ABCD的四边长分别为a ,b, c,
d,则这个四边形的面积为:
思考:以上公式对任意的四边形是否都成立?
八、课后作业
南宋时期的数学家秦九韶独立发现的计算三角形面积的“三斜求积
术”,与著名的海伦公式等价,其求法是:“以小斜幂并大斜幂减中斜幂,
余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实.一为从隅,
开平方得积.”若把以上这段文字写成公式,
在 中,若 D在AC上,且BD平分
则 的面积=________; BD=____________.
[针对训练] 南宋时期的数学家秦九韶独立发现的计算三角形面积的“三斜求积术”,
与著名的海伦公式等价,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘
于上,以小斜幂乘大斜幂减上,余四约之,为实.一为从隅,开平方得积.”若把
以上这段文字写成公式, 已知 的三边分别a,b,c.
面积为S.若 且
则 的面积为=_______.
.
1.2 应用举例—海伦与秦九韶公式
一.阅读引领,师生探究.
我国南宋著名数学家秦九韶(约1202—1261),在他的著作《算数九章》卷五“田域类 ”里有这样一个题目:
“问有沙田一段,有三斜.其小斜一十三里,中斜一十四里,
大斜一十五里.里法三百步.欲知几何.”意思是已知一个三
角形的三边长分别为13里,14里,15里,则这个沙田的
面积为多少?
思考:如何将上述问题转化为数学问题呢?
A
小斜一十三里
中斜一十四里
B
C
大斜十五里
能否用已学的数学知识来解决这个数学问题?
A
c
b
B
C
a
海伦公式:已知 三边长分
别为a, b, c,则 的面积为:
其中
海伦的生平
海伦(Heron),古希腊数学家.生
卒于亚历山大城.他擅长测量,给出
了多种求图形面积和体积的定理和公
式,最著名的是已知三边长求三角形
面积的海伦公式.海伦有许多学术著
.主要著作有《量度论》,《体积求法》,《几何》等.
????
二.古希腊数学
古希腊的数学发展到亚历山大里亚时期,数学的应用性得 到了很大的发展,其突出的一点就是三角术的发展.三角术是人们为了建立定量的天文学,以便用来预报天体的运行路线和位置以帮助报时,计算日历、航海和研究地理而产生的.
在解三角形问题中.一个比较困难的问题是如何由三角形的三边a, b, c,直接求出三角形的面积.据说这个问题最早是由古希腊数学家阿基米德解决的,他得到了公式:
但现在人们常常以古希腊的数学家海伦命名这个公式,称此公式为海伦公式,因为这个公式最早出现在海伦的著作《测地术》中,并在海伦的著作《测量仪器》和《度量术》中给出证明,海伦公式的特点是形式很美,大家很容易记住公式.
,其中
思考:通过你对古希腊数学文化的了解,对于已知三角形三边求三角形面积的数学问题你是否有一定的启发?
三、学习中国文化,增强民族自信心
我国南宋著名数学家秦九韶(约1202—1261)在他的著作《算
数九章》也提到了与海伦公式等价的从三角形的三边求面积的公
式,他把这种方法称为“三斜求积”,《算数九章》中的求法是:
“以小斜幂并大斜幂减中斜幂,余半之,自乘于上.以小斜幂乘大
斜幂减上,余四约之,为实.一为从隅,开平方的积.”如果把以上
这段文字写成公式,就是:
三斜求积公式与公元1世纪古希腊数学家海伦给出的公式殊途
同归,他虽然与海伦公式形式上不一样,但两者完全等价.它填
补了我国传统数学的空白,从中可以充分说明我国古代已具有
很高的数学水平.
思考:怎样证明这两个公式相等?
,其中
秦九韶生平
秦九韶,字道古.鲁郡(今河南范县)人. 中国古代
数学家.南宋嘉定元年(1208年)生;约景定(1261
年)年被贬至梅州,咸淳四年(1268)二月,在梅州辞
世,时年61岁.
《算数九章》 全书九章十八卷,九章九类:“大衍类”、
“天时类”、“田域类”、“测望类”、“赋役类”、“钱谷类”、
“营建类”、“军旅类”、“市物类”,每类9题(9问)共计
81题(81问),该书内容丰富至极,上至天文、星象、
历律、测候,下至河道、水利、建筑、运输,尤其是系统总结和发展了高次方程的数值
解法与一次同余问题的解法,提出了相当完备.”正负开方术”和”大衍求一术”对数学发展
产生了广泛的影响.
大衍求一术
秦九韶的“大衍求一术”,被康托尔称为“最幸运的天才”.秦九韶所发明的“大衍求一术”,即现代数中一次同余式组解法,是中世纪世界数学的成就之一,比西方1801年著名数学家高斯(Gauss,1777—1855年)建立的同余理论早554年,被西方称为“中国剩余定理”
正负开方术
秦九韶在《数书九章》中除“大衍求一术”外,还创拟了正负开方术,即任意高次方程的数值解法,秦九韶所发明的此项成果比1819年英国人霍纳(W·G·Horner,1786—1837年)的同样解法早572年.
秦九韶的成就也代表了中世纪世界数学发展的主流与最高水平,在世界数学史上占有崇高的地位.
四、合作探究
,其中
古希腊数学家海伦运用平面知识,证明海伦面积公式.中国古代数学家秦九韶
只给出公式,用来解决已知三角形三边求三角形面积这类问题的计算.
你能通过已学知识给出秦九韶面积公式的证明吗?
证明:如图,在△ABC中,过A作高AD交BC于D,
设 ,那 么 .
由于AD是△ABD、△ACD的公共边.
五、应用举
南宋时期的数学家秦九韶独立发现的计算三角形面积的“三斜求积
术”,与著名的海伦公式等价,其求法是:“以小斜幂并大斜幂减中斜幂,
余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实.一为从隅,
开平方得积.”若把以上这段文字写成公式,
若 的周长为
用“三斜求积术”求 面积=________;
[针对训练]中国宋代的数学家秦九韶曾提出“三斜求积术”,即假设在平面内有
一个三角形,边长分别为a,b,c.三角形的面积可由公式
求得,其中p为三角形周长的一半,这个公式也被称为海伦-秦九韶公式,现有一个三
角形的边长满足 则此三角形面积的最大值=_________.
六、师生小结
,其中
<2>秦九韶:南宋著名数学家,代表作《算数九章》''三斜求积术“已知
三边长求三角形面积
<1>海伦(Heron):古希腊数学家主要著作有《量度论》,《体积求法》,《几何》
等,最著名的是已知三边长求三角形面积的海伦公式.
七、知识拓展与提升
若将海伦公式推广到四边形,即设四边形ABCD的四边长分别为a ,b, c,
d,则这个四边形的面积为:
思考:以上公式对任意的四边形是否都成立?
八、课后作业
南宋时期的数学家秦九韶独立发现的计算三角形面积的“三斜求积
术”,与著名的海伦公式等价,其求法是:“以小斜幂并大斜幂减中斜幂,
余半之,自乘于上,以小斜幂乘大斜幂减上,余四约之,为实.一为从隅,
开平方得积.”若把以上这段文字写成公式,
在 中,若 D在AC上,且BD平分
则 的面积=________; BD=____________.
[针对训练] 南宋时期的数学家秦九韶独立发现的计算三角形面积的“三斜求积术”,
与著名的海伦公式等价,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘
于上,以小斜幂乘大斜幂减上,余四约之,为实.一为从隅,开平方得积.”若把
以上这段文字写成公式, 已知 的三边分别a,b,c.
面积为S.若 且
则 的面积为=_______.
.
