人教版数学九年级上册 第二十三章 旋转 旋转作图与计算讲义(无答案)
文档属性
| 名称 | 人教版数学九年级上册 第二十三章 旋转 旋转作图与计算讲义(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 517.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-29 23:33:38 | ||
图片预览



文档简介
教师辅导讲义
学员编号: 年 级: 课 时 数: 学员姓名: 辅导科目: 学科教师:
授课类型 T同步( 旋转作图 ) C专题( 旋转计算 )
授课日期及时段
教学内容
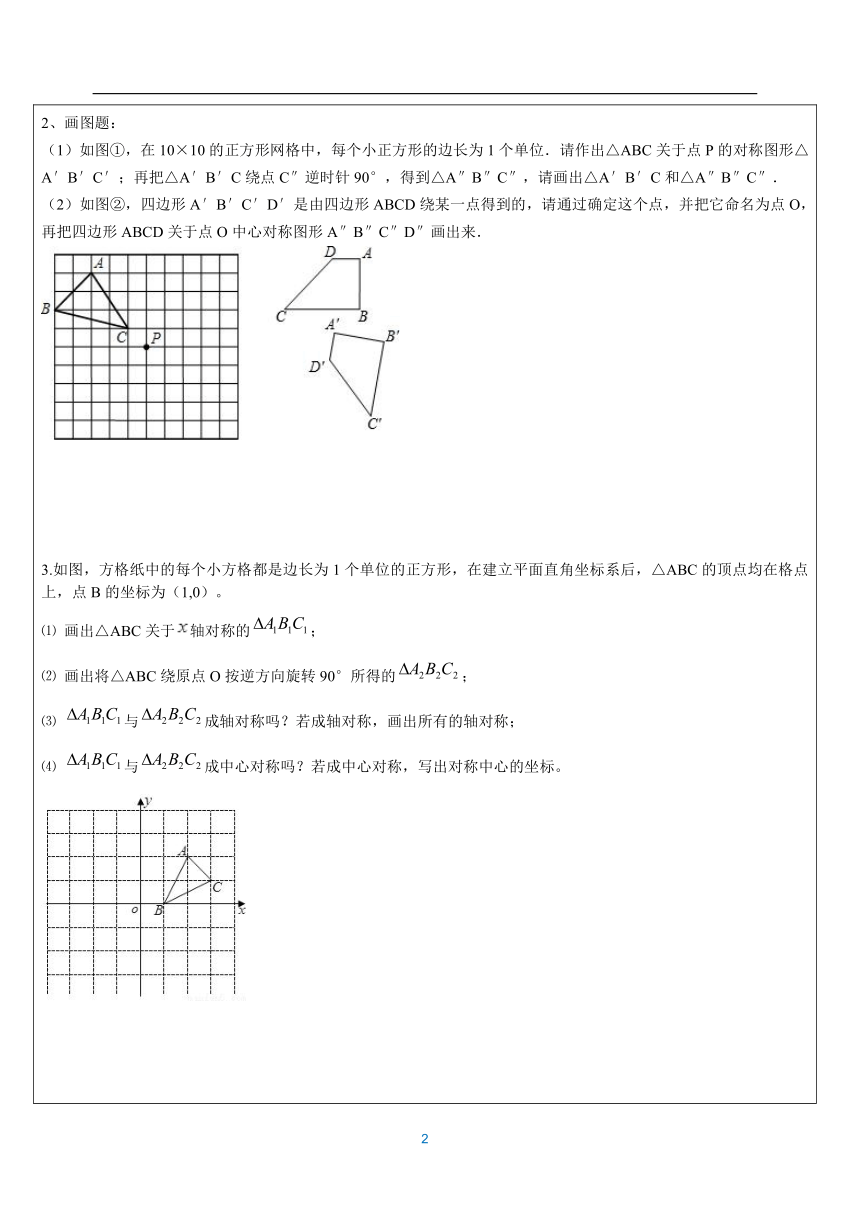
(热个身先~~~) 1、ABCD绕坐标原点O按顺时针方向旋转180°后得到四边形A1B1C1D1.
(1)直接写出D1点的坐标;
(2)将四边形A1B1C1D1平移,得到四边形A2B2C2D2,若D2(4,5),画出平移后的图形.(友情提示:画图时请不要涂错阴影的位置哦!)
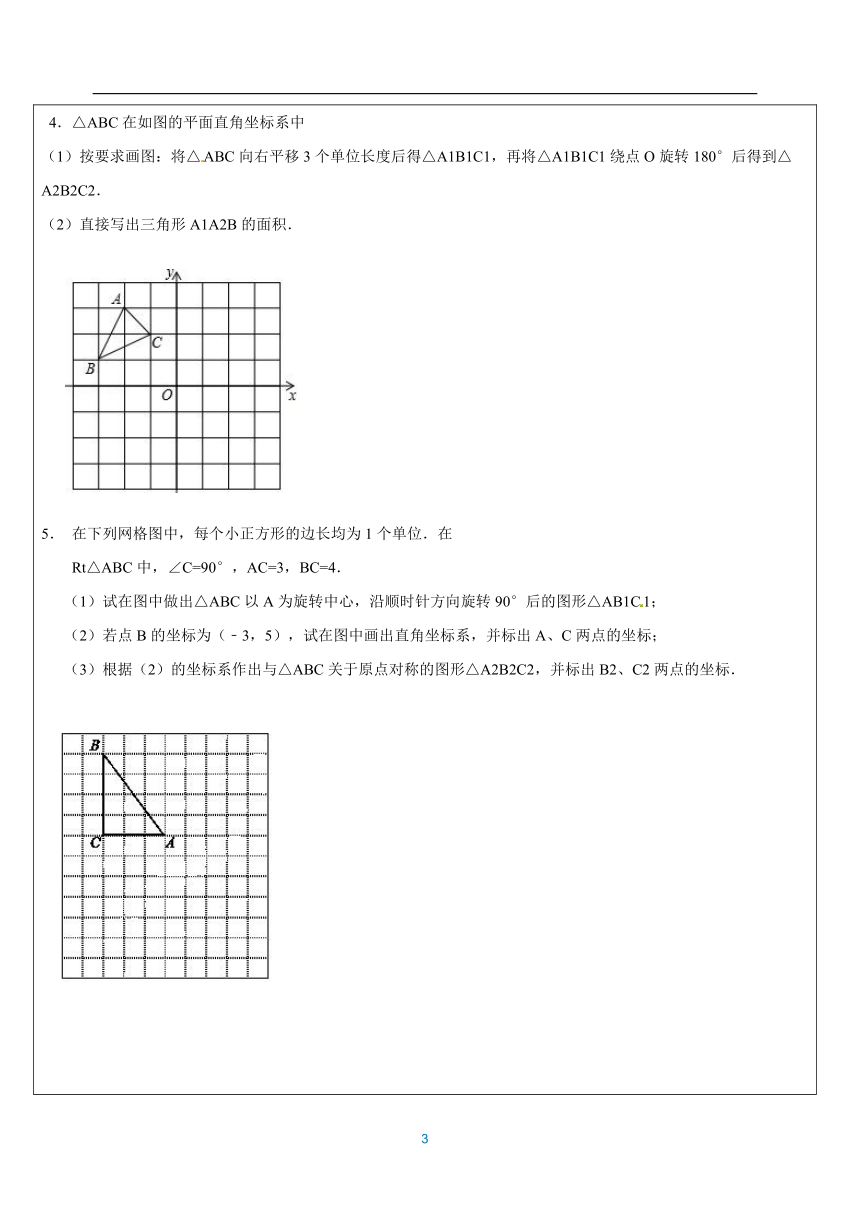
2、画图题:
(1)如图①,在10×10的正方形网格中,每个小正方形的边长为1个单位.请作出△ABC关于点P的对称图形△A′B′C′;再把△A′B′C绕点C″逆时针90°,得到△A″B″C″,请画出△A′B′C和△A″B″C″.
(2)如图②,四边形A′B′C′D′是由四边形ABCD绕某一点得到的,请通过确定这个点,并把它命名为点O,再把四边形ABCD关于点O中心对称图形A″B″C″D″画出来.
3.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)。 ⑴ 画出△ABC关于轴对称的; ⑵ 画出将△ABC绕原点O按逆方向旋转90°所得的; ⑶ 与成轴对称吗?若成轴对称,画出所有的轴对称; ⑷ 与成中心对称吗?若成中心对称,写出对称中心的坐标。 4.△ABC在如图的平面直角坐标系中 (1)按要求画图:将△ABC向右平移3个单位长度后得△A1B1C1,再将△A1B1C1绕点O旋转180°后得到△A2B2C2. (2)直接写出三角形A1A2B的面积. 5. 在下列网格图中,每个小正方形的边长均为1个单位.在 Rt△ABC中,∠C=90°,AC=3,BC=4. (1)试在图中做出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1; (2)若点B的坐标为(﹣3,5),试在图中画出直角坐标系,并标出A、C两点的坐标; (3)根据(2)的坐标系作出与△ABC关于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标. 6、如图所示,网格中有一个四边形和两个三角形.
(1)请你画出三个图形关于点O的中心对称图形;
(2)将(1)中画出的图形与原图形看成一个整体图形,请写出这个整体图形对称轴的条数;这个整体图形至少旋转多少度与自身重合. 7、在如图的方格中,每个小正方形的边长都是1.
(1)△ABC与△A1B1C1是否构成中心对称图形?若是,请在图中画出对称中心O;
(2)在图中画出将△A1B1C1沿直线DE向上平移5格得到的△A2B2C2;
(3)要使△A2B2C2与△CC1C2重合,需将△A2B2C2绕点C2顺时针,则至少要旋转多少度;
(4)请出△ABC的周长和面积. ( 画竹必先成竹于胸!) 1、如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标; (2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2; (3)求出(2)中C点旋转到C2点所经过的路径长(记过保留根号和π). 2、如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上.建立平面直角坐标系后,点A的坐标为(-4,1),点B的坐标为(-1,1).
(1)请画出△ABC关于y轴对称的△A1B1C1.
(2)将△ABC绕点O逆时针90°后得到△A2B2C2,试在图中画出图形△A2B2C2,并点C到点C2所经过的路径长.(结果保留π) 3、如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).将△ABC绕坐标原点O逆时针90°,得到△A′B′C′,画出△A′B′C′.并点A经过的路径长度 4、如图,方格纸中每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图所示.
(1)在图中作出△ABC关于y轴对称的△A1B1C1,并直接写出点A1的坐标.
(2)将△ABC绕点O顺时针90°得△A2B2C2,在图中作出△A2B2C2,并点A到点A2所经过的路径长. 5、△ABC的三个顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1).
(1)在图中画出将△ABC先向右平移3个单位,再向上平移2个单位后得到的△A1B1C1;
(2)在图中画出△ABC绕原点O顺时针90°后得到的△A2B2C2;
(3)在(2)的条件下,点A所经过的路径的长度. 6、如图,在边长为1的小正方形组成的网格中,△ABC的顶点均在格点上,请按要求完成下列各题:
(1)以直线BC为对称轴作△ABC的轴对称图形,得到△A1BC,再将△A1BC绕着点B逆时针90°,得到△A2BC2,请在下面网格中画出△A1BC、△A2BC2;
(2)求线段BC到BC1过程中,C点所经过的路线长度(结果用含有π的式子表示). 7、如图,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)(﹣2,1),先将沿一确定方向平移得到,点B的对应点的坐标是(1,2),再将绕原点O顺时针旋转90°得到,点的对应点为点. (1)画出; (2)画出; (3)求出在旋转过程中,点到达的路径长. 8.△ABC在直角坐标系内的位置如图所示. (1)分别写出A、B、C的坐标; (2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标; (3)请在这个坐标系内画出△A2B2C2,使△A2B2C2与△ABC关于原点对称,并写出A2的坐标; (4)求△ABC的面积. 9.如图,在方格纸中,每个小正方形的边长都为1个单位长度,△ABC与△A1B1C1呈中心对称.
(1)若将△ABC绕某一点O180°可得到△A1B1C1,请直接在图上标出此点O;
(2)作出将△A1B1C1沿直线DE方向向上平移5个单位长度得到的△A2B2C2;
(3)要使△A2B2C2与△CC1C2重合,则△A2B2C2绕点C2顺时针方向 度,并出△A2B2C2扫过的面积. 10.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A、B、C都在格点上,将△ABC绕点A按顺时针方向90°得到△AB'C'.
(1)在正方形网格中,画出△AB'C';
(2)线段AB在过程中所扫过的面积. 11.如图,将小旗ACDB放于平面直角坐标系中,得到各顶点的坐标为A(-6,12),B(-6,0),C(0,6),D(-6,6).以点B为旋转中心,在平面直角坐标系内将小旗顺时针旋转90°.?
(1)画出旋转后的小旗A′C′D′B′;?
(2)写出点A′,C′,D′的坐标;?
(3)求出线段BA旋转到B′A′时所扫过的扇形的面积. 12.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点). (1)将△ABC绕点B顺时针旋转90°得到△A′BC′, 请画出△A′BC′. (2)求BA边旋转到BA′位置时所扫过图形的面积. 13. (?http:?/??/?a.hiphotos.baidu.com?/?zhidao?/?pic?/?item?/?9e3df8dcd100baa125afab0a4410b912c9fc2e84.jpg" \o "点击查看大图" \t "http:?/??/?zhidao.baidu.com?/?_blank?)如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,9).
(1)画出△ABC饶点A顺时针旋转90°后得到的△,并写出三点的坐标;
(2)求出△ABC在上述旋转过程中扫过的面积。 14.如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C. (1)画出△A1B1C,直接写出点A1、B1的坐标; (2)求在旋转过程中,△ABC所扫过的面积. 8、如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C. (1)画出△A1B1C,直接写出点A1、B1的坐标;(2)求在旋转过程中,△ABC所扫过的面积. 9、△ABC三个顶点A、B、C在平面直角坐标系中位置如图所示.将△ABC向下平移2个单位后得到,绕点顺时针旋转90°得到.
(1)求出△ABC的面积, 画出、,并写出的坐标, 旋转过程中,求出扫过的图形面积。 10.每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上.(题中结果均保留根号和π)
(1)按要求:作出△ABC关于原点成中心对称的中心对称图形△A1B1C1;
(2)△A1B1C1中顶点B1坐标为 (3)求(1)后A点到A1的路径长;
(4)求(1)中OB旋转后到OB1扫过的面积.
11.如图,在边长为1的正方形组成的网格中,△AOB的顶点均在格点上,点A,B的坐标分别是A(3,3)、B(1,2),△AOB绕点O逆时针旋转90°后得到△?. (1)画出△,直接写出点,的坐标; (2)在旋转过程中,点B经过的路径的长; (3)求在旋转过程中,线段AB所扫过的面积.
T同步——旋转作图
同步题型分析
C专题——旋转计算
知识典例
1
同课章节目录
