人教版数学九年级上册第二十三章 旋转 旋转模型讲义(无答案)
文档属性
| 名称 | 人教版数学九年级上册第二十三章 旋转 旋转模型讲义(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 992.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-29 00:00:00 | ||
图片预览



文档简介
教师辅导讲义
学员编号: 年 级: 课 时 数: 学员姓名: 辅导科目: 学科教师:
授课类型 C专题( 旋转运用 ) C专题( 旋转模型 )
授课日期及时段
教学内容
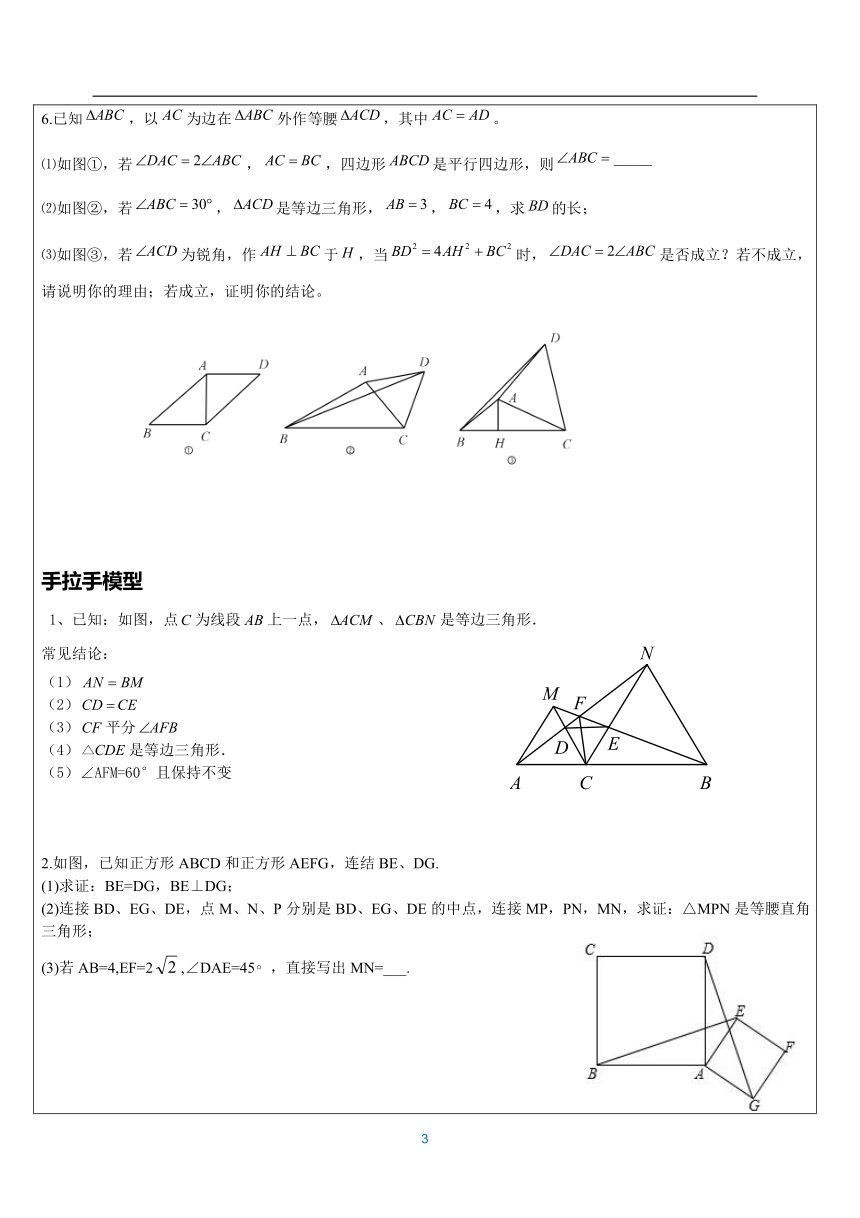
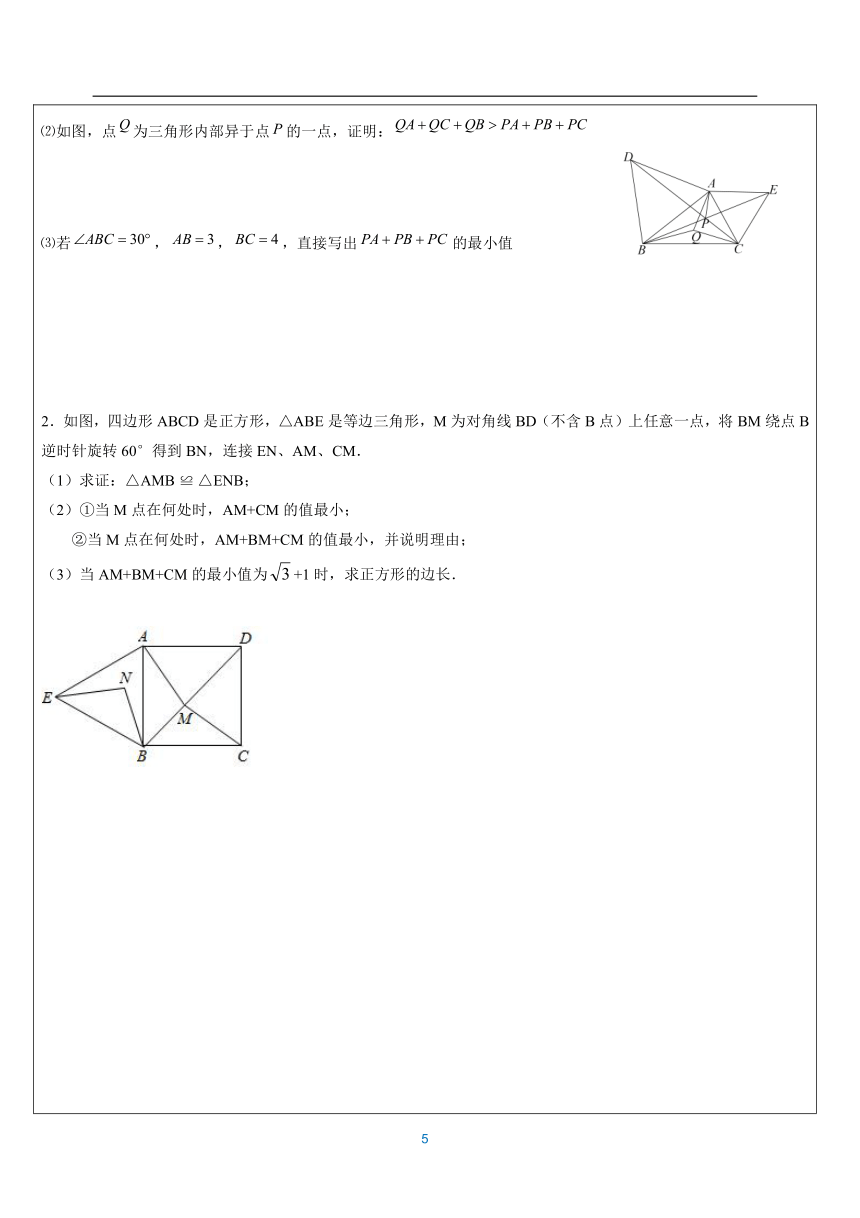
(课堂精粹) 图形中出现有公共端点的相等线段,可考虑将含有相等线段的图形绕公共端点旋转 两相等线段的夹角后与另一相等线段重合.遇60度旋60度,造等边三角形;遇90度旋90度,造等腰直角;遇等腰旋顶点,造旋转全等 1.如图,在中,,,是内的一点,且,求的度数. 2.如图,D为等边三角形ABC内的一点,DA=5,DB=4,DC=3,将线段AD以点A为旋转中心逆时针旋转60°得到线段AD',下列结论:①点D与点D'的距离为5;②∠ADC=150°;③△ACD'可以由△ABD绕点A逆时针旋转60°得到;④点D到CD'的距离为3;⑤S四边形ADCD′=6+,其中正确的有( )A.2个 B.3个 C.4个 D.5个3.如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,过E点作EH⊥CD于H,则EH的长为 .4.如图,在凸四边形中,,. 求证: 5.如图所示,为正方形内一点,若,,.求:(1) 的度数;(2)正方形的面积. 6.已知,以为边在外作等腰,其中。⑴如图①,若,,四边形是平行四边形,则⑵如图②,若,是等边三角形,,,求的长;⑶如图③,若为锐角,作于,当时,是否成立?若不成立,请说明你的理由;若成立,证明你的结论。 手拉手模型 1、已知:如图,点为线段上一点,、是等边三角形.常见结论: (1)(2)(3)平分(4)是等边三角形.(5)∠AFM=60°且保持不变 2.如图,已知正方形ABCD和正方形AEFG,连结BE、DG. (1)求证:BE=DG,BE⊥DG; (2)连接BD、EG、DE,点M、N、P分别是BD、EG、DE的中点,连接MP,PN,MN,求证:△MPN是等腰直角三角形;(3)若AB=4,EF=2,∠DAE=45?,直接写出MN=___. 3.如图1,我们把对角线互相垂直的四边形叫做垂美四边形。 (1)概念理如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由。 (2)性质探究:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系。 猜想结论:(要求用文字语言叙述)___ 写出证明过程(先画出图形,写出已知、求证). 问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长。 费马点问题1.阅读下列材料对于任意的,若三角形内或三角形上有一点,若有最小值,则取到最小值时,点为该三角形的费马点。 ①若三角形内有一个内角大于或等于,这个内角的顶点就是费马点 ②若三角形内角均小于,则满足条件时,点既为费马点 解决问题: ⑴如图,中,三个内角均小于,分别以、为边向外作等边、,连接、交于点,证明:点为的费马点。(即证明)且 ⑵如图,点为三角形内部异于点的一点,证明: ⑶若,,,直接写出的最小值 2.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM. (1)求证:△AMB ≌ △ENB; (2)①当M点在何处时,AM+CM的值最小; ②当M点在何处时,AM+BM+CM的值最小,并说明理由; (3)当AM+BM+CM的最小值为+1时,求正方形的边长. 3.【操作发现】:如图 1 中,只要证明△DAB 是等边三角形即可; 【类比探究】:如图 2 中,以 PA 为边长作等边△PAD,使 P、D 分别在 AC 的两侧,连接 CD.利 用全等三角形的性质以及三角形的三边关系即可解决问题; 【解决问题】:如图 3 中,将△APB 绕点 A 按逆时针方向旋转 60°,得到△AP′C′,只要证明 ∠PP′C=90°,利用勾股定理即可解决问题; 【拓展应用】:如图 4 中,先由旋转的性质得出△APC≌△EDC,则∠ACP=∠ECD,AC=EC=4,∠PCD=60°,再证明∠BCE=90°,然后在 Rt△BCE 中,由勾股定理求出 BE 的长度,即为 PA+PB+PC 的最小值; 1.如图,将一块含45°角的三角尺的底角顶点固定在正方形ABCD的顶点A处,一直角边AP和斜边AQ分别与正方形的对角线BD交于点E、F,且DF=2,BE=3,求EF的长度.2、在正方形ABCD中,点E、F分别在边BC、CD上,且∠EAF=∠CEF=45°, 将△ADF绕着点A顺时针旋转90°,得到△ABG,如图1,求证:△AEG≌△AEF;若直线EF与AB、AD的延长线分别交于点M,N,如图2,求证: 将正方形改为长与宽不相等的矩形,若其余条件不变,请你直接写出线段EF,BE,DF之间的数量关系。 3.在等边的两边AB,AC所在直线上分别有两点M,N,D为外一点,且,,,探究:当点M,N分别爱直线AB,AC上移动时,BM,NC,MN之间的数量关系及的周长与等边的周长L的关系.⑴如图①,当点M,N在边AB,AC上,且DM=DN时,BM,NC,MN之间的数量关系式__________;此时=__________⑵如图②,当点M,N在边AB,AC上,且时,猜想(1)问的两个结论还成立吗?写出你的猜想并加以证明;⑶如图③,当点M,N分别在边AB,CA的延长线上时,若AN=x,则Q=_________(用x,L表示) 图(1) 图(2) 图(3) 1、已知:,平分. ⑴在图1中,若,证明:. ⑵在图2中,若,,探究、、三者之间的数量关系,并给出证明; ⑶在图3中:若(),,则(用含的三角函数表示,直接写出结果,不必证明)2、如图1,正方形和正方形,是正方形的对称中心,MN交于,QM交于. ⑴猜想:与的数量关系 ⑵如图2,若将原题中的“正方形”改为“菱形”,且,其它条件不变,探索线段与线段的数量关系,并加以证明. ⑶如图3,若将原题中的“正方形”改为“矩形”,且,其它条件不变,探索线段与线段的数量关系,并说明理由. ⑷如图4,若将原题中的“正方形”改为平行四边形,且,,其它条件不变,求出的值(直接写出答案) 直三角形中点1.在等腰直角中,,,是的中点,点从出发向运动, 交于点,试说明的形状和面积将如何变化. 2.等腰直角三角形,为中点,,求的周长. 已知Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC、CB(或延长线)于E、F. 当∠EDF绕D点旋转到DE⊥AC于E时(如图1),易证.当∠EDF绕D点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立? 若成立,请给予证明;若不成立, , , 又有怎样的数量关系?请写出你的猜想,不需证明. ( 画竹必先成竹于胸!) 1.如图,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.(1)如图1,点E,F在AB,AC上,且∠EDF=90°.求证:BE=AF;(2)点M,N分别在直线AD,AC上,且∠BMN=90°.①如图2,当点M在AD的延长线上时,求证:AB+AN=AM;②当点M在点A,D之间,且∠AMN=30°时,已知AB=2,直接写出线段AM的长. 2.问题:如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,试判断BE、EF、FD之间的数量关系.【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图(1)证明上述结论.【类比引申】如图(2),四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足 关系时,仍有EF=BE+FD.【探究应用】如图(3),在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分别有景点E、F,∠EAF=75°且AE⊥AD,DF=40米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:≈1.41,≈1.73) 3.在正方形ABCD中,点P在射线AC上,作点P关于直线CD的对称点Q,作射线BQ交射线DC于点E,连接BP. (1)当点P在线段AC上时,如图1. ①依题意补全图1; ②若EQ=BP,则∠PBE的度数为 ,并证明; (2)当点P在线段AC的延长线上时,如图2.若EQ=BP,正方形ABCD的边长为1, 请写出求BE长的思路.(可以不写出计算结果) 4.如图,正方形ABCD中,点E是BC边上的一个动点,连接AE,将线段AE绕点A逆时针旋转90°,得到AF,连接EF,交对角线BD于点G,连接AG. (1)根据题意补全图形;(2)判定AG与EF的位置关系并证明; (3)当AB = 3,BE = 2时,求线段BG的长. 1.如图,在△ABC中,AB=AC,∠C=70°,△AB′C′与△ABC关于直线EF对称,∠CAF=10°,连接BB′,则∠ABB′的度数是( ) A.30° B.35° C.40° D.45° 2.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=116°,则∠α的大小是( )A.64° B.36° C.26° D.22°3.如图①,正方形A的一个顶点与正方形B的对称中心重合,重叠部分面积是正方形A面积的,如图②,移动正方形A的位置,使正方形B的一个顶点与正方形A的对称中心重合,则重叠部分面积是正方形B面积的( )A. B. C. D. 4.如图,把△ABC绕着点A顺时针方向旋转,得到△A B 'C ',点C恰好在B 'C '上,旋转角为α,则∠C '的度数为 (用含α的式子表示). 5.如图, 在Rt△ABC中,∠C=90°,AC= BC,将Rt△ABC绕点A逆时针旋转15°得到Rt△,交AB于E,若图中阴影部分面积为,则的长为_____. 6如图,将边长为的正方形绕点B逆时针旋转30°,那么图中阴影部分的面积为 ( ) A.3 B.C.3- D.3-7.在平面直角坐标系中,点绕坐标原点顺时针旋转后,恰好落在右图中阴影区域(包括边界)内,则的取值范围是 . 8.如图,四边形ABCD为正方形,AB=1,把△ABC绕点A逆时针旋转60°得到△AEF,连接DF,则DF的长为( )A. B. C. D. 9.如图,正方形ABCD的边长为,点E是正方形ABCD内一点,将△BCE绕着点C顺时针旋转90°,点E的对应点F和点B,E三点在一条直线上,BF与对角线AC相交于点G,若DF=6,则GF的长为 .10.如图,AB=AC,∠CAB=90°,∠ADC=45°,AD=1,CD=3,则BD= . 11.如图,将等边△ABC绕点C顺时针旋转90°得到△EFC,∠ACE的平分线CD交EF于点D,连接AD、AF.(1)求∠CFA度数;(2)求证:AD∥BC. 12.将一副三角尺的直角重合放置(∠B=30°,∠C=45°),如图1所示,(1)图1中∠BEC的度数为 ;(2)三角尺AOB的位置保持不动,将三角尺COD绕其直角顶点O顺时针方向旋转: ①当旋转至图2所示位置时,恰好OD∥AB,求此时∠AOC的大小; ②若将三角尺COD继续绕O旋转,直至回到图1位置,在这一过程中,是否会存在△COD其中一边能与AB平行?如果存在,请你画出图形,并直接写出相应的∠AOC的大小;如果不存在,请说明理由. 13.在四边形ABCD中,AB∥CD,∠ABC=60°,AB=BC=4,CD=3.(1)如图1,求△BCD的面积;(2)如图2,M是CD边上一点,将线段BM绕点B逆时针旋转60°,可得线段BN,过点N作NQ⊥BC,垂足为Q,设NQ=n,BQ=m,求n关于m的函数解析式.(自变量m的取值范围只需直接写出)
C专题——旋转模型
等线段共点模型
半角模型
对角互补模型
F
B
C
E
D
A
图1
B
A
E
C
F
D
图2
图3
E
B
A
D
F
C
知识典例
达标检测
1
同课章节目录
