人教版数学九年级上册24.1 圆的性质讲义 (无答案)
文档属性
| 名称 | 人教版数学九年级上册24.1 圆的性质讲义 (无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 863.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-29 23:32:58 | ||
图片预览


文档简介
教师辅导讲义
学员编号: 年 级: 课 时 数: 学员姓名: 辅导科目: 学科教师:
授课类型 T同步(圆的基本性质) C专题(垂径定理)
授课日期及时段
教学内容
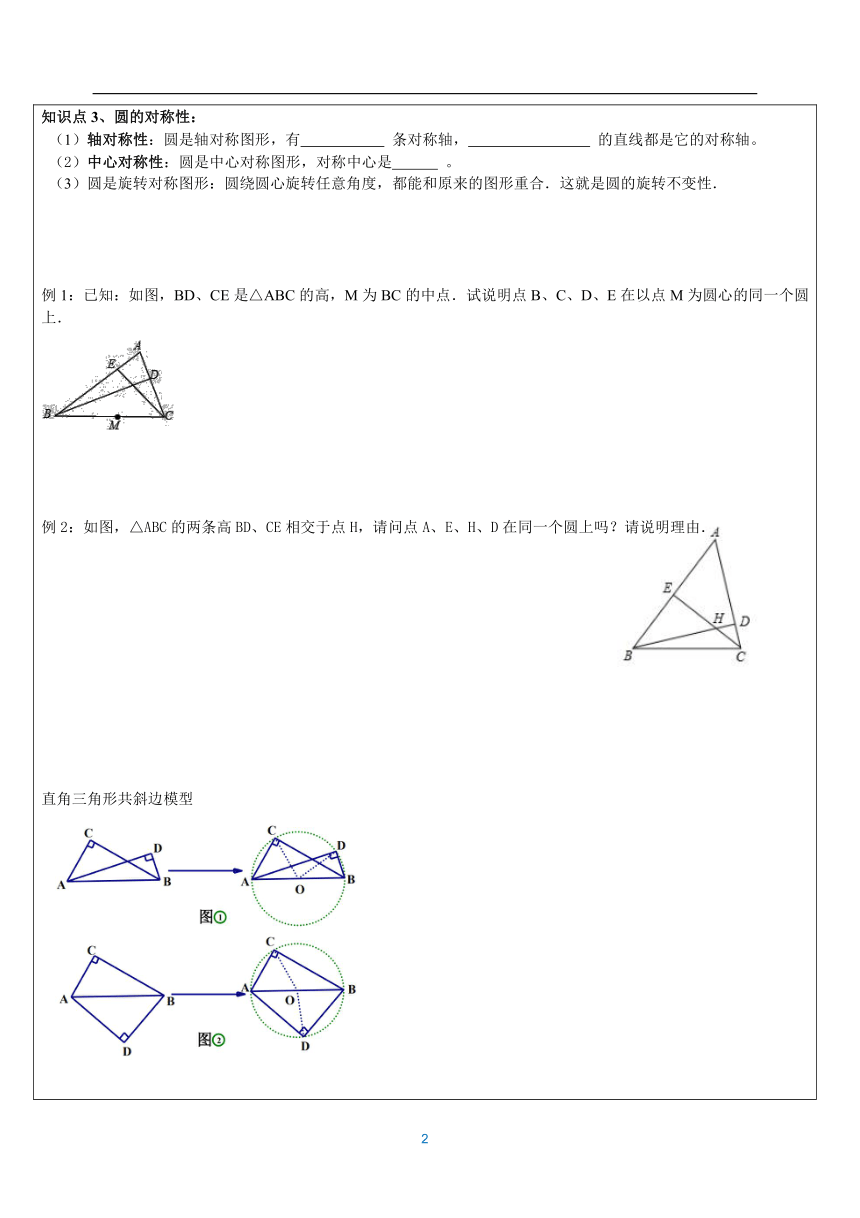
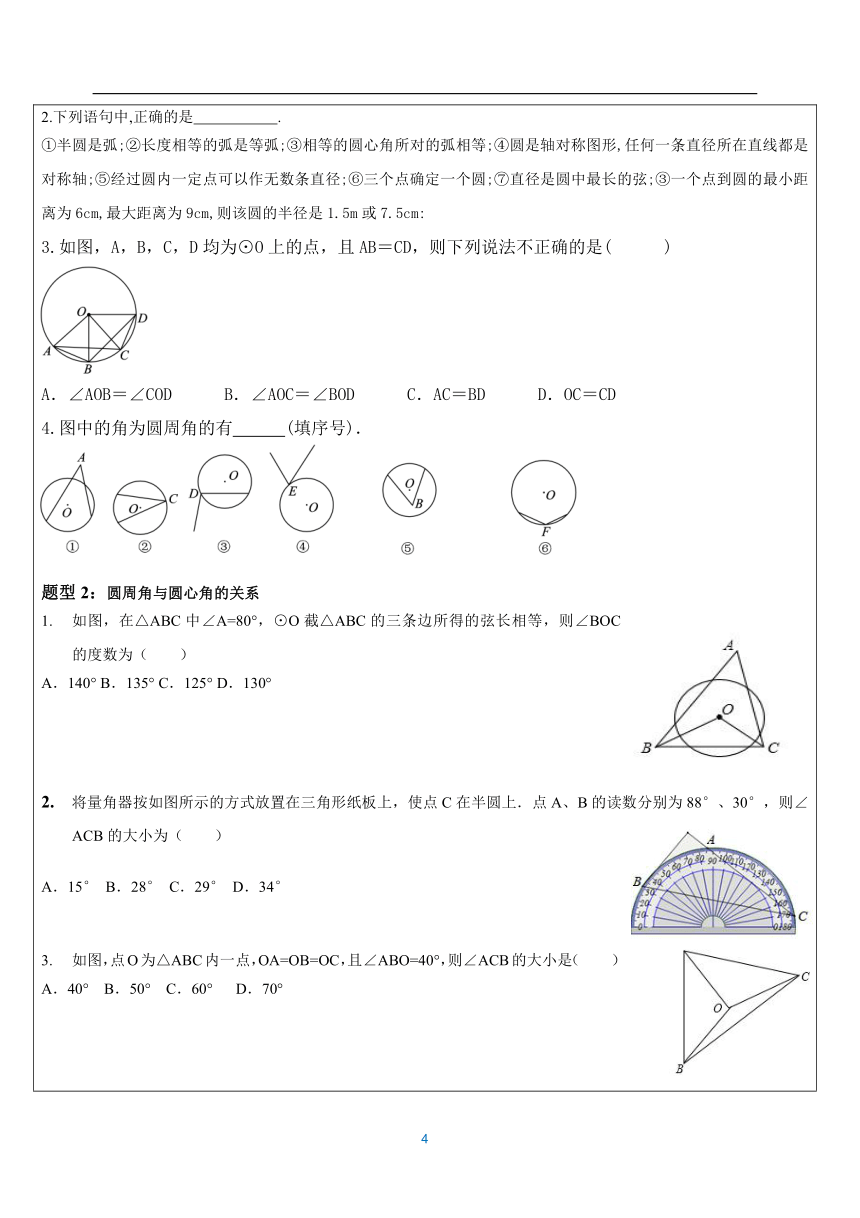
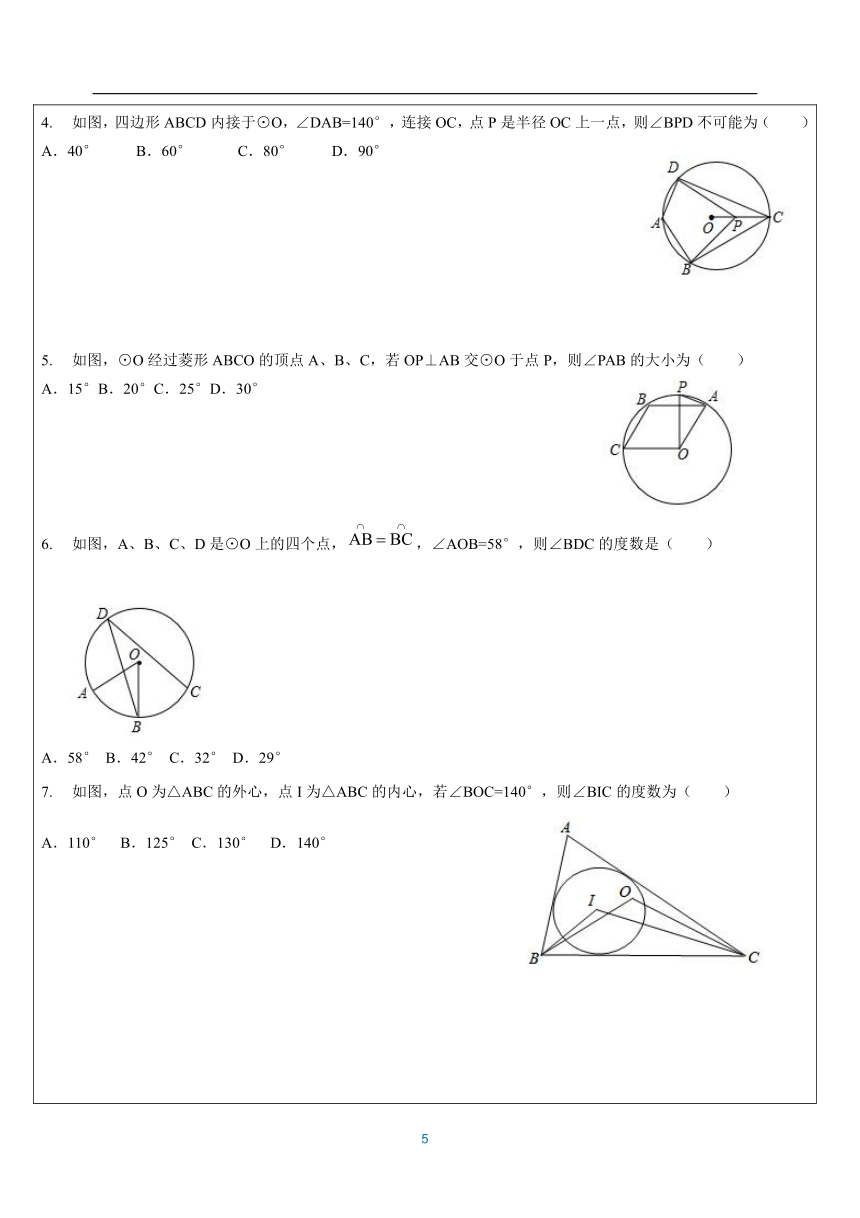
知识点1、 圆的定义:1、描述性定义 在一个平面内,线段OA绕它固定一个端点O旋转一周,另一个端点A所形成的图形叫做圆,其中固定的端点O叫做圆心,线段OA叫做半径。 2、集合性定义 圆可以看作是到定点的距离等于定长的点的集合; 3、圆的表示方法 以点O为圆心的圆,记作“⊙”,读作“圆” 【特别注意】:1、在一个圆中,圆心决定圆的 ,半径决定圆的 。直径是圆中 的弦,弦不一定是直径。 知识点2、弦与弧:(1)弦:连结圆上任意两点的线段叫做弦 (2)直径:经过圆心的弦叫做直径,并且直径是同一圆中最长的弦,直径等于半径的2倍. (3)弧:圆上任意两点间的部分叫做圆弧,简称弧,以为端点的弧记作,读作弧AB。 (4)半圆:圆的任意一条直径的两个端点把圆分成两条弧,每条弧都叫做半圆。 (5)等圆:能够重合的两个圆叫做等圆。 (6)等弧:在同圆或等圆中,能够重合的弧叫做等弧。 知识点3、圆的对称性: (1)轴对称性:圆是轴对称图形,有 条对称轴, 的直线都是它的对称轴。 (2)中心对称性:圆是中心对称图形,对称中心是 。 (3)圆是旋转对称图形:圆绕圆心旋转任意角度,都能和原来的图形重合.这就是圆的旋转不变性. 例1:已知:如图,BD、CE是△ABC的高,M为BC的中点.试说明点B、C、D、E在以点M为圆心的同一个圆上. 例2:如图,△ABC的两条高BD、CE相交于点H,请问点A、E、H、D在同一个圆上吗?请说明理由. 直角三角形共斜边模型模型分析 (1)共斜边的两个直角三角形,同侧或异侧,都会得到四点共圆; (2)四点共圆后可以根据圆周角定理得到角度相等,完成角度等量关系的转化,是证明角相等重要的途径之一知识点4、与圆有关的角(1)圆心角:顶点在圆心的角叫圆心角。圆心角的性质:圆心角的度数等于它所对的弧的度数。 圆周角:顶点在圆上,两边都和圆相交的角叫做圆周角。 二、圆心角定理与圆周角定理1.圆心角定理:在同圆或等圆中,同弧所对的圆心角相等。相等的圆心角所对的弧相等 ,所对的弦也相等. 2.圆心角定理的逆定理:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一对量相等,那么它们所对应的其余各对量都相等. 圆心角所对的弧叫做10的弧,n0的圆心角所对的弧就是n0的弧. 2.圆周角定理 ①圆周角等于它所对的弧所对的圆心角的一半. ②同弧或等弧所对的圆周角相等;在同圆或等圆中,相等的圆周角所对的弧相等. 圆周角定理的推论:90°的圆周角所对的弦为直径;半圆或直径所对的圆周角为直角. 三、圆内接四边形 如果一个四边形的四个顶点在同一个圆上,那么这个四边形叫做圆的内接四边形,这个圆叫做四边形的外接圆.圆内接四边形的对角互补. 四、多边形与圆内接多边形 1.各边相等,各个角也相等的多边形叫做正多边形. 2.我们把经过一个正多边形的所有顶点的圆叫做这个正多边形的外接圆,这个正多边形也就叫做圆内接正多边形. 题型1:圆的有关概念1.下列语句,错误的是( ) A.直径是弦 B.相等的圆心角所对的弧相等 C.弦的垂直平分线一定经过圆心 D.平分弧的半径垂直于弧所对的弦 2.下列语句中,正确的是 .①半圆是弧;②长度相等的弧是等弧;③相等的圆心角所对的弧相等;④圆是轴对称图形,任何一条直径所在直线都是对称轴;⑤经过圆内一定点可以作无数条直径;⑥三个点确定一个圆;⑦直径是圆中最长的弦;③一个点到圆的最小距离为6cm,最大距离为9cm,则该圆的半径是1.5m或7.5cm:3.如图,A,B,C,D均为⊙O上的点,且AB=CD,则下列说法不正确的是( ) A.∠AOB=∠COD B.∠AOC=∠BOD C.AC=BD D.OC=CD4.图中的角为圆周角的有 (填序号). 题型2:圆周角与圆心角的关系如图,在△ABC中∠A=80°,⊙O截△ABC的三条边所得的弦长相等,则∠BOC的度数为( ) A.140° B.135° C.125° D.130° 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为88°、30°,则∠ACB的大小为( ) A.15° B.28° C.29° D.34° 如图,点O为△ABC内一点,OA=OB=OC,且∠ABO=40°,则∠ACB的大小是( ) A.40° B.50° C.60° D.70° 如图,四边形ABCD内接于⊙O,∠DAB=140°,连接OC,点P是半径OC上一点,则∠BPD不可能为( )A.40° B.60° C.80° D.90° 如图,⊙O经过菱形ABCO的顶点A、B、C,若OP⊥AB交⊙O于点P,则∠PAB的大小为( ) A.15°B.20°C.25°D.30° 如图,A、B、C、D是⊙O上的四个点,,∠AOB=58°,则∠BDC的度数是( ) A.58° B.42° C.32° D.29° 如图,点O为△ABC的外心,点I为△ABC的内心,若∠BOC=140°,则∠BIC的度数为( ) A.110° B.125° C.130° D.140° 题型3:圆心角、弦、弧的关系如图,BC是半圆O的直径,D,E是上两点,连接BD,CE并延长交于点A,连接OD,OE.如果∠A=70°,那么∠DOE的度数为( )A.35° B.38° C.40° D.42°如图,AB,CD是⊙O的直径,,若∠AOE=32°,则∠COE的度数是( ) A.32° B.60° C.68° D.64° 如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是( ) A.AB=AD B.BC=CD C. D.∠BCA=∠DCA 如图,AB是⊙O的直径,C,D分别是⊙O上的两点,OC⊥OD,AC=2cm,BD=cm,则⊙O的半径是() B.2cm C. D.3cm 如图,AB是⊙O的直径,BC是⊙O的弦.若BD=2,CD=6,则BC的长为( ) B. C. D.如图,AB是⊙O的直径,∠BOD=120°,点C为弧BD的中点,AC交OD于点E,DE=1,则AE的长为( ) B. C. D. 如图,已知AB和CD是⊙O的两条等弦.OM⊥AB,ON⊥CD,垂足分别为点M、N,BA、DC的延长线交于点P,联结OP.下列四个说法中:①;②OM=ON;③PA=PC;④∠BPO=∠DPO,正确的个数是( )A.1 B.2 C.3 D.4 题型4:圆内接多边形的性质如图,四边形ABCD为⊙O的内接四边形,∠AOC=110°,则∠ADC=( ) A.55° B.110° C.125° D.70° 如图,四边形ABCD是⊙O的内接四边形,已知∠BCD=110°,则∠BOD的度数为( )A.70° B.90° C.110° D.140° 如图,四边形ABCD内接于⊙O,F是上一点,且,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为( ) A.45° B.50° C.55° D.60° 半径相等的圆内接正三角形、正方形、正六边形的边长之比为( ) A.1∶∶ B.∶∶1 C.3∶2∶1 D.1∶2∶3 如图,⊙O是正五边形ABCDE的外接圆,则∠CAD= °.如图,四边形ABCD内接于⊙O,延长CO交圆于点E,连接BE.若∠A=100°,∠E=60°,则∠OCD的度数为( ) A.30° B.50° C.60° D.80°如图所示,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是( ) A.80° B.120° C.100° D.90° 如图,A、B、C、D是⊙O上的四点,BD为⊙O的直径,若四边形ABCO是平行四边形,则∠ADB的大小为( ) A.30° B.45° C.60° D.75° 如图,A,B是⊙O上的两点,C是⊙O上不与A,B重合的任意一点.如果∠AOB=130°,那么∠ACB的度数为( )A.65° B.115° C.130° D.65°或115° 如图,在圆内接四边形ABCD中,若∠A∶∠B∶∠C=2∶3∶6,则∠D等于( ) A.67.5° B.135° C.112.5° D.45° 如图,四边形ABCD是⊙O内接四边形,D是中点,E是上一点,若∠CED=40°,则∠ADC= 度. 如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC= . 如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°. (1)判断△ABC的形状,并证明你的结论. (2)证明:PA+PB=PC. 垂径定理:(1)垂径定理 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧. (2)垂径定理的推论 推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧. 推论2:弦的垂直平分线经过圆心,并且平分弦所对的两条弧. 推论3:平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.【特别注意:1、垂径定理及其推论实质是指一条直线满足:⑴过圆心⑵垂直于弦⑶平分弦⑷平分弦所对的优弧⑸平分弦所对的劣弧五个条件中的两个,那么可推出其中三个,注意解题过程中的灵活运用;2、圆中常作的辅助线是过圆心作弦的垂线;3、垂径定理常用作计算,在半径r、弦a、弦心d、和拱高h中已知两个可求另外两个】垂径定理常见模型 已知 AB 是⊙O 的一条弦,过点 O 作 OE⊥AB,连接OA(OB)则 模型分析:在解决求弦长、弦心距、半径问题时,在圆中常作弦心距或连接 半径作为辅助线,利用弦心距、半径和半弦组成一个直角三角形,再利用勾 股定理进行计算。 例1:如图,用直角三角板经过两次画图找到圆形工件的圆心,这种方法应用的道理是( ) A.垂径定理 B.勾股定理 C.直径所对的圆周角是直角 D.90°的圆周角所对的弦是直径 二、同步题型分析 题型1:垂径定理如图在⊙O中,弦AB=8,OC⊥AB,垂足为C,且OC=3,则⊙O的半径( )A. 5 B. 10 C. 8 D. 6已知⊙O的半径为10,P为⊙O内一点,且OP=6,则过P点,且长度为整数的弦有( )5条 B. 6条 C. 8条 D. 10条 P为⊙O内一点,且OP=2,若⊙O的半径为3,则过点P的最短的弦是( )A.1 B.2 C. D.⊙O的半径为5cm,弦AB//CD,且AB=8cm,CD=6cm,则AB与CD之间的距离为( )1 cm B. 7cm C. 3 cm或4 cm D. 1cm 或7cm ⊙O的半径为5cm,AB、CD是⊙O的两条弦,AB∥CD,AB=8cm,CD=6cm.那么求得AB和CD之间的距离为____. ⊙O内的一点P,且OP=3,⊙O的半径为5,则过点P最短的弦长_______,最长的弦为______,过点P的整数弦有_________条. 已知:⊙O的半径为6cm,点P是⊙O外一点,且OP=9cm. (1)以点P为圆心,作⊙P与⊙O外切,求小圆⊙P的半径是多少? (2)以点P为圆心,作⊙P与⊙O内切,求大圆⊙P的半径是多少?已知圆O的半径为5,P为圆O内一点,且OP=3,则过点P的所有弦中,弦长是整数的共有( )A.4条 B.3条 C.2条 D.1条 如图OC是⊙O的半径,弦AB⊥OC于点D,点E在⊙O上,EB恰好经过圆心O.连接EC.若∠B=∠E,OD=,则劣弧AB的长为()A.2л B.4л C.6л D.9л如图,在⊙O中,已知弦AB长为16cm,C为的中点,OC交AB于点M,且OM:MC=3:2,则CM长为( )A.2cm B.4cm C.6cm D.8cm 如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )3cm B. cm C. 2.5cm D. cm 如图,在⊙O中直径AB=8,弦AC=CD=2,则BD长为( ) B.6 C. D.如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx+12与⊙O交于B、C两点,则弦BC长的最小值( )A.24 B.10 C.8 D.25 如图,C是以AB为直径的半圆O上任意一点,AB=3,则△ABC周长的最大值是( ) B. C. D.9如图,AB为弓形AB的弦,AB=,弓形所在圆⊙O的半径为2,点P为弧AB上动点,点I为△PAB的内心,当点P从点A向点B运动时,点I移动的路径长为_______。如图,圆形纸片⊙O半径为5,先在其内剪出2个边长相等的最大正方形,再在剩余部分剪出2个边长相等的最大正方形,4个正方形面积总和为________。如图,在⊙O中,弦AB=1,点C在AB上移动,连结OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为______。如图,⊙O的两条弦AB∥CD(AB不是直径),点E为AB中点,连结EC,ED(1)直线EO与AB垂直吗?请说明理由; (2)求证:EC=ED. 如图,OD是⊙O的半径,AB是弦,且OD⊥AB于点C连接AO并延长交⊙O于点E,若AB=8,CD=2,求⊙O半径OA的长.如图,Rt△ABC中,∠ACB=90°,O为△ABC角平分线的交点,以OC为半径的⊙O交△ABC于D、E、F、G.(1)求证:CD=EF; (2)若⊙O的半径为,AE=2,求AB的长. 如图,BE是⊙O的直径,半径OA⊥弦BC,点D为垂足,连AE,EC.(1)若∠AEC=28°,求∠AOB的度数;(2)若∠BEA=∠B,BC=6,求⊙O的半径. 如图,四边形CDEF是弓形的内接正方形,已知弓形的弦AB长为8,弓形的高HG为2. (1)求弓形所在圆的半径长; (2)求正方形CDEF的边长. 如图,在圆O中,弦AB=8,点C在圆O上(C与A,B不重合),连接CA、CB,过点O分别作OD⊥AC,OE⊥BC,垂足分别是点D、E. (1)求线段DE的长; (2)点O到AB的距离为3,求圆O的半径. 如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA. (1)求证:∠ABD=2∠BDC; (2)过点C作CE⊥AB于H,交AD于E,求证:EA=EC; (3)在(2)的条件下,若OH=5,AD=24,求线段DE的长如图,AB是⊙O的一条弦,且AB=点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA.(1)求OA的长; (2)若AF是⊙O的另一条弦,且点O到AF的距离为,求∠BAF的度数. 如图,△ABC内接于⊙O,弦CD平分∠ACB,点E为弧AD上一点,连接CE、DE,CD与AB交于点N. (1)如图1,求证:∠AND=∠CED; (2)如图2,AB为⊙O直径,连接BE、BD,BE与CD交于点F,若2∠BDC=90°-∠DBE,求证:CD=CE;
T同步——圆的基本性质
同步知识梳理
同步题型分析
C专题——垂径定理
专题导入
1
同课章节目录
