人教版数学九年级上册24.4 圆的计算讲义(无答案)
文档属性
| 名称 | 人教版数学九年级上册24.4 圆的计算讲义(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-29 00:00:00 | ||
图片预览



文档简介
教师辅导讲义
学员编号: 年 级: 课 时 数: 学员姓名: 辅导科目: 学科教师:
授课类型 T同步(弧长扇形面积计算) C专题(正多边形与圆) T能力(阴影部分面积)
授课日期及时段
教学内容
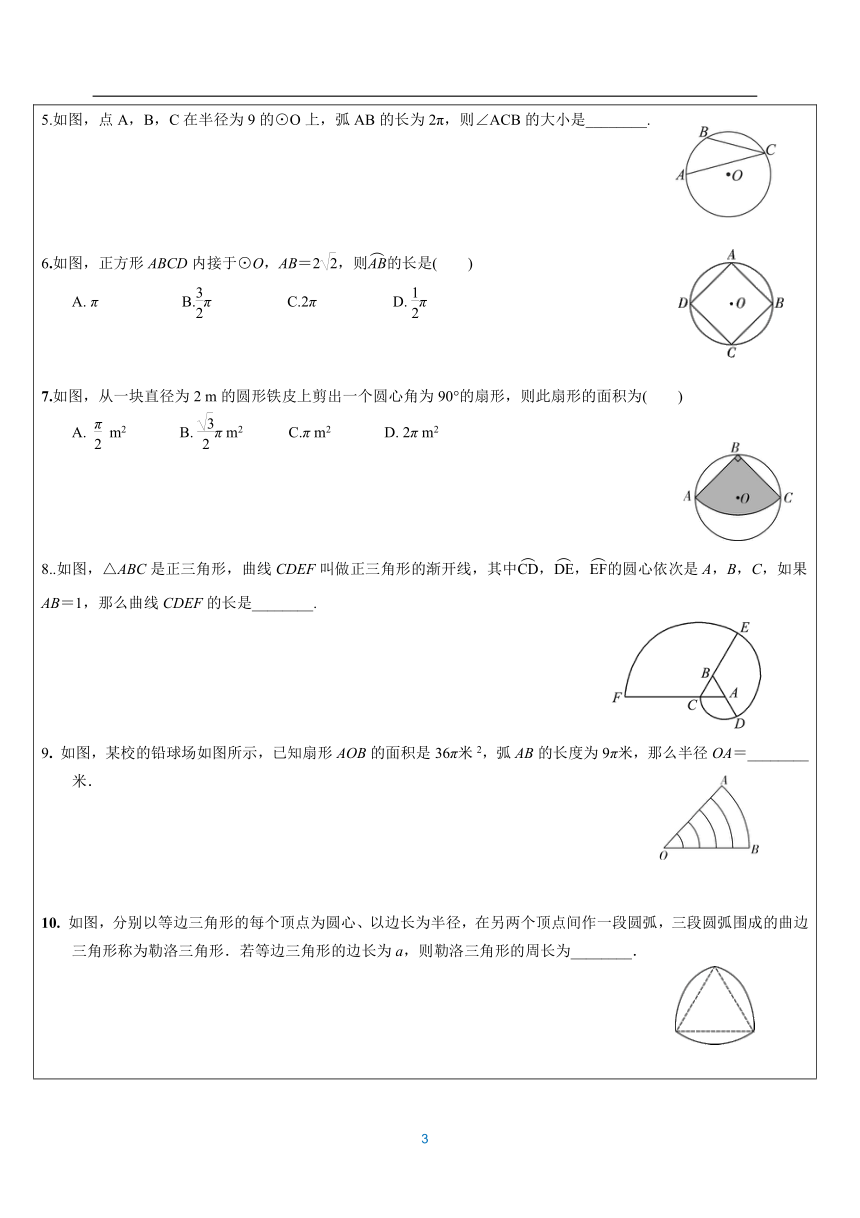
(大脑放电影~) 弧长、扇形面积的计算1.半径为R的圆中,°的圆心角所对的弧长l的计算公式为l=________. 2.扇形的面积 (1)半径为R的圆中,圆心角为°的扇形面积为:S扇形=________; (2)半径为R,弧长为l的扇形面积为:S扇形=________.圆柱、圆锥的有关计算1.设圆柱的高为l,底面半径为r,如图1,则有: (1)S圆柱侧=________; (2)S圆柱全=________________. 2.设圆锥的母线长为l,底面半径为r,高为h,如图2,则有: (1)S圆锥侧=________; (2)S圆锥全=________________. (3)侧面展开后,扇形的圆心角度数_________; (热个身先~~~) 弧长、扇形的计算【例1】如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,BO=4,则弧BD的长为( ) ( )A.π B.π C.2π D.π 【例2】如图,已知⊙O的半径是2,点A,B,C在⊙O上,若四边形OACB为菱形,则图中阴影部分面积为( )A.π-2 B.π- C.π-2 D.π- 1.一个扇形的圆心角是120°,面积为3π cm2,那么这个扇形的半径是( ) A.1 cm B.3 cm C.6 cm D.9 cm2.一个扇形的弧长是10π cm,面积是60π cm2,则此扇形的圆心角的度数是( ) A.300° B.150° C.120° D.75°3.如图,⊙O的半径为3,四边形ABCD内接于⊙O,连结OB,OD,若∠BOD=∠BCD,则的长为( )π B.π C.2π D.3π 4. 如图,一段公路的转弯处是一段圆弧(),则的展直长度为( )A. 3π m B. 6π m C.9π m D. 12π m 5.如图,点A,B,C在半径为9的⊙O上,弧AB的长为2π,则∠ACB的大小是________. 6.如图,正方形ABCD内接于⊙O,AB=2,则的长是( )A. π B.π C.2π D. π 7.如图,从一块直径为2 m的圆形铁皮上剪出一个圆心角为90°的扇形,则此扇形的面积为( )A. m2 B. π m2 C.π m2 D. 2π m2 8..如图,△ABC是正三角形,曲线CDEF叫做正三角形的渐开线,其中,,的圆心依次是A,B,C,如果AB=1,那么曲线CDEF的长是________. 9. 如图,某校的铅球场如图所示,已知扇形AOB的面积是36π米2,弧AB的长度为9π米,那么半径OA=________米. 10. 如图,分别以等边三角形的每个顶点为圆心、以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为a,则勒洛三角形的周长为________. 11. 如图,公园内有一个半径为20米的圆形草坪,A,B是圆上的点,O为圆心,∠AOB=120°,从A到B只有路,一部分市民为走“捷径”,踩坏了花草,走出了一条小路AB.通过计算可知,这些市民其实仅仅少走了________步.(假设1步为0.5米,结果保留整数.参考数据:≈1.732,π取3.142) 12.如图,已知等边△ABC的边长为6,以AB为直径的⊙O与边AC,BC分别交与D,E两点,则劣弧DE的长为______. 13.如图,已知⊙O的半径为2,A为⊙O外一点.过点A作⊙O的一条切线AB,切点为B,AO的延长线叫⊙O于点C.若∠BAC=30°,则劣弧BC的长为______. 14.如图,⊙O的直径AB=6,若∠BAC=50°,则劣弧AC的长为( ) A.2π B. C. D.15.如图,点O是圆形纸片的圆心,将这个圆形纸片按下列顺序折叠,使和都经过圆心O,则阴影部分的面积是☉O面积的?( ) ? ?A. ????B.? ????C.? ????D.? 16.有一张矩形纸片ABCD,其中AD=8 cm,上面有一个以AD为直径的半圆,正好与对边BC相切.如图(甲),将它沿DE折叠,使A点落在BC上,如图(乙),这时,半圆还露在外面的部分(阴影部分)的面积是( ) A. cm2 B. cm2 C.(π-2) cm2 D.(π-4) cm217.如图,正方形ABCD的边长为1,分别以顶点A,B,C,D为圆心,1为半径画弧,四条弧交于点E,F,G,H,则图中阴影部分的外围周长为__________.18.如图,矩形ABCD中,AB=4,BC=3,F是AB中点,以点A为圆心,AD为半径作弧交AB于点E,以点B为圆心,BF为半径作弧交BC于点G,则图中阴影部分面积的差S1-S2为__________. 圆锥的相关计算1.已知圆锥的母线长为6,将其侧面沿着一条母线展开后所得扇形的圆心角为120°,则该扇形的面积是( )A. 4π B. 8π C. 12π D. 16π2.一个圆锥的侧面积是底面积的3倍,则圆锥侧面展开图对应的扇形的圆心角是( ) A.120° B.180° C.240° D.300°3. 如图,圆锥的母线长为10 cm,高为8 cm,则该圆锥的侧面展开图(扇形)的弧长________cm.(结果用π表示) 4.用一块圆心角为216°的扇形铁皮,做一个高为40 cm的圆锥形工件(接缝忽略不计),那么这个扇形铁皮的半径是________cm.5. 如图,用一个半径为20 cm,面积为150π cm2的扇形铁皮,制作一个无底的圆锥(不计接头损耗),则圆锥的底面半径r为________cm.6. 如图,8×8的正方形网格纸上有扇形OAB和扇形OCD,点O、A、B、C、D均在格点上,若用扇形OAB围成一个圆锥的侧面,记这个圆锥的底面半径为r1;若用扇形OCD围成另一个圆锥的侧面,记这个圆锥的底面半径为r2,则的值为________.7.如图,把一个圆锥沿母线OA剪开,展开后得到扇形AOC,已知圆锥的高h为12 cm,OA=13 cm,则扇形AOC中的长是__________cm.(结果保留π) 8.现有一张圆心角为108°,半径为40 cm的扇形纸片,小红剪去圆心角为θ的部分扇形纸片后,将剩下的纸片制作成一个底面半径为10 cm的圆锥形纸帽(接缝处不重叠),则剪去的扇形纸片的圆心角θ为__________. (你都掌握了没有呢~~~) 1.水平地面上有一面积为30π cm2的扇形AOB,半径OA=6 cm,且OA与地面垂直,在没有滑动的情况下,将扇形向右滚动至OB与地面垂直为止,则点O移动的距离为 ________. 2.在矩形ABCD中,AB=5,AD=12,将矩形ABCD按图中所示的方式在直线l上进行两次旋转,则点B在两次旋转过程中经过的路径的长是________.3.正六边形硬纸片ABCDEF在桌面上由图①的起始位置沿直线l不滑行地翻滚一周后到图②的位置.若正六边形的边长为2 cm,则正六边形的中心O运动的路程为________cm. . 4.如图,矩形ABCD的外接圆O与水平地面相切于点A,已知圆O的半径为4,且=2.若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了66π,则此时与地面相切的弧为( ) A. B. C. D. 5.将Rt△AOB 如图放置在直角坐标系中,并绕O点顺时针旋转90°至△COD的位置,已知A(-2,0),∠ABO =30°.则ΔAOB旋转过程中所扫过的图形的面积为( ) A. B. C. D. 6.如图,点A1的坐标为(2,0),过点A1作x轴的垂线交直线l:y=于点B1,以原点O为圆心,OB1的长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;….按此作法进行下去,则的长是______________. 7.如图,Rt△ABC的边BC位于直线l上,AC=,∠ACB=90°,∠A=30°.若Rt△ABC由现在的位置向右滑动地旋转,当点A第3次落在直线l上时,点A所经过的路线的长为 )π(结果用含有π的式子表示)
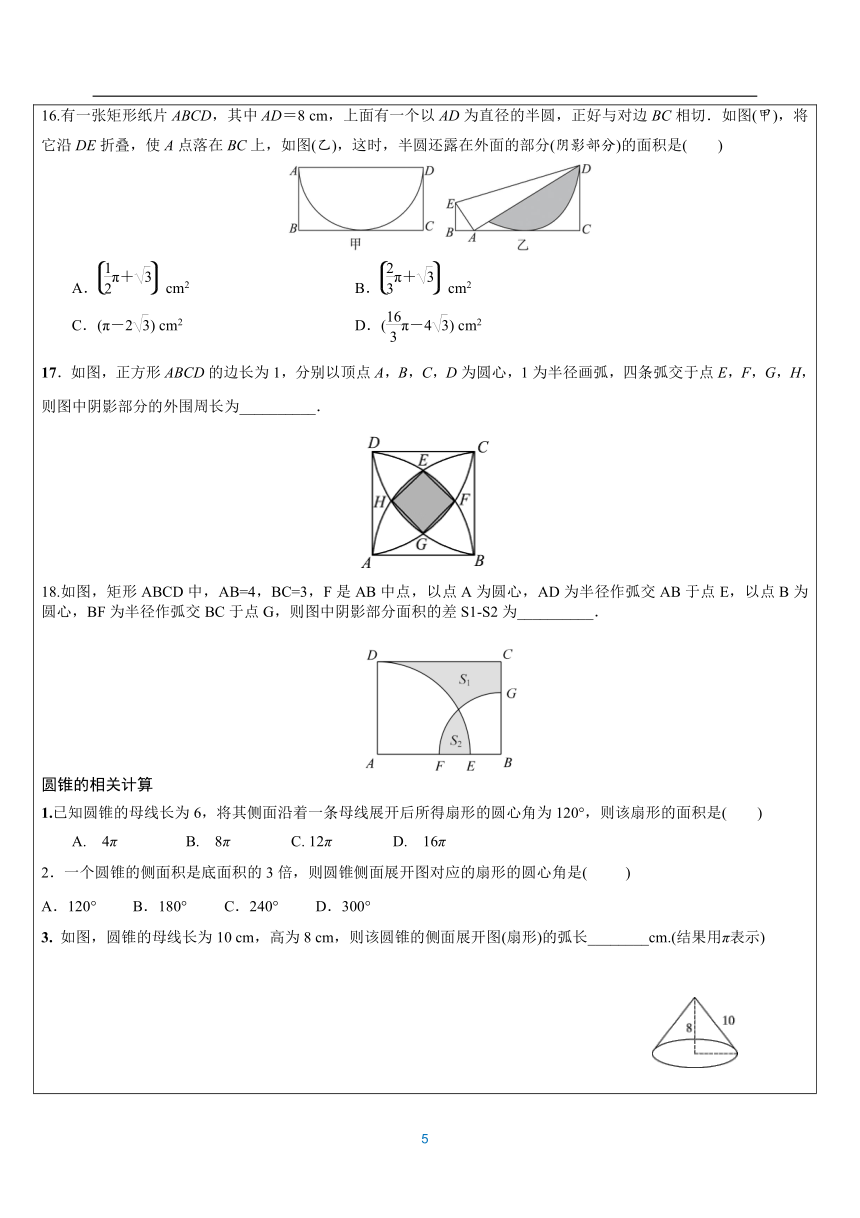
8.如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2 017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( ) A.2 017π B.2 034π C.3 024π D.3 026π9.如图,正△ABO的边长为2,O为坐标原点,A在x轴上,B在第二象限,△ABO沿x轴正方向作无滑动的翻滚,经第一次翻滚后得到△A1B1O,则翻滚2017次后AB中点M经过的路径长为______. (课堂精粹) 正多边形的有关计算1.定义 各边都相等且________也相等的多边形是正多边形 2.性质正多边形都是轴对称图形,正偶数多边形是________对称图形 中心角==每个外角的度数 每个内角的度数=________ 3.作法 将圆周n等分,依次连接各等分点,首尾相接得到正n边形 ( 画竹必先成竹于胸!) 【例4】如图,正方形ABCD内接于半径为2的⊙O,则图中阴影部分的面积为( ) A.π+1 B.π+2 C.π-1 D.π-21.如图,正方形ABCD内接于⊙O,AB=2,则的长是 ( ) A.π B.π C.2π D.π2.如图,一张半径为1的圆形纸片在边长为的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是( )【例2】如图,六边形ABCDEF为⊙O的内接正六边形,若⊙O的半径为,则阴影部分的面积为 .[来源:Z§xx§k.Com] 1.如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为( )A. B. C. D. 【例3】如图,P,Q分别是⊙O的内接正五边形的边AB,BC上的点,BP=CQ,则∠POQ=__________. 1.如图,⊙O是边长为1的正方形ABCD的外接圆,P为弧AD上的不同于A、D的任意一点,则PA+PB+PC+PD的值为( )A. 2 B. 4 C. 6 D. 82.如图,正五边形ABCDE和正三角形AMN都是⊙O的内接多边形,则∠BOM= .3.如图,正方形ABCD和等边三角形AEF都内接于⊙O,若⊙O的半径为2,则的长为 ( 举一反三增能力! )1.如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.(1)求证:AD平分∠BAC; (2)若CD=1,求图中阴影部分的面积(结果保留π). 2.如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,E为⊙O上一点,过点E作直线DC,分别交AM,BN于点D,C,且CB=CE.(1)求证:DA=DE; (2)若AB=6,CD=4,求图中阴影部分的面积. 3.如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D,OB与⊙O相交于点E.(1)求证:AC是⊙O的切线; (2)若BD=,BE=1,求阴影部分的面积. 4.如图,在⊙O中,半径OA⊥OB,过点OA的中点C作FD∥OB交⊙O于D,F两点,且CD=,以O为圆心,OC为半径作,交OB于E点. (1)求⊙O的半径OA的长; (2)计算阴影部分的面积. 5.如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为点D,AD交⊙O于点E,连结CE. (1)判断CD与⊙O的位置关系,并证明你的结论; (2)若E是的中点,⊙O的半径为1,求图中阴影部分的面积. 6.如图,以△ABC的边AB为直径画⊙O,交AC于点D,半径OE∥BD,连接BE,DE,BD,设BE交AC于点F,若∠DEB=∠DBC.(1)求证:BC是⊙O的切线; (2)若BF=BC=2,求图中阴影部分的面积. (比一比!) 阴影部分面积的四种求法 (1)公式法 (2)等积变形法 整体法 (4)割补法 1.如图,在?ABCD中,∠B=60°,⊙C的半径为3,则图中阴影部分的面积是( )A. π B. 2πC.3π D. 6π2.如图所示,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )A. π-4 B. π-1C.π-2 D. π-2 3. 如图,AB为半圆的直径,且AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )A. π B. 2π C. D. 4π4.如图,正方形ABCD内接于⊙O,⊙O的半径为2,以点A为圆心,以AC长为半径画弧交AB的延长线于点E,交AD的延长线于点F,则图中阴影部分的面积是( )A. 4π-4 B. 4π-8C.8π-4 D. 8π-8 5.如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,则图中阴影部分的面积是( )A. 18+36π B. 24+18πC.18+18π D. 12+18π6.如图,扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交于点D,以OC为半径的交OA于点E,则图中阴影部分的面积是( )A. 12π+18 B. 12π+36C.6π+18 D. 6π+36 7.如图,在边长为4的正方形ABCD中,以点B为圆心,以AB为半径画弧,交对角线BD于点E,则图中阴影部分的面积是________(结果保留π). 8.如图,在矩形ABCD中,BC=4,CD=2,以AD为直径的半圆O与BC相切于点E,连接BD,则阴影部分的面积为______.(结果保留π) 9.如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC=2,把△ABC绕点A按顺时针方向旋转45°后得到△AB′C′,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是________. 10.如图,Rt△ABC,∠B=90°,∠C=30°,O为AC上一点,OA=2,以O为圆心,以OA为半径的圆与CB相切于点E,与AB相交于点F,连接OE、OF,则图中阴影部分的面积是________. 11.运用图形变化的方法研究下列问题:如图,AB是?⊙O的直径,CD、EF是?⊙O的弦,且?,?,?,?.则图中阴影部分的面积是(????) B、 C、 D、12.如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )A. - B. - C.π- D.π-
13.如图,在Rt△ABC中,∠ACB=90°,AC=BC=1.将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE,点B经过的路径为?弧BD,则图中阴影部分的面积是( ) B. C. D. 14.如图在Rt△ABC中,∠BCA=90°,∠BAC=30°,BC=2,将Rt△ABC绕点A顺时针旋转90°得到Rt△ADE,则BC扫过的区域(阴影部分)的面积为( )A. B.(2-)π C.π D.π 15.在矩形ABCD中,AB=,BC=2,以点A为圆心,AD为半径画弧交线段BC于点E,连结DE,则阴影部分的面积为( )A.- B.- C.π- D.π- 16.在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB延长线上的点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连结EF,CG.(1)求证:EF∥CG;(2)求点C,点A在旋转过程中形成的,与线段CG所围成的阴影部分的面积.17.如图,在△ABC中,∠ACB=90°,AC=BC=2,将△ABC绕AC的中点D逆时针旋转90°得到△A'B'C',其中点B的运动路径为?,则图中阴影部分的面积为_____???. 18.如图,AB为半圆O的直径,C为AO的中点,CD⊥AB交半圆于点D,以C为圆心,CD为半径画弧交AB于E点,若AB=4,则图中阴影部分的面积是( ) A.π+ B.π C.π? D.π 19.如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=6,EF=8,FC=10,则正方形与其外接圆之间形成的阴影部分的面积为__________________. 20.小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他绘制了如图2所示的图形.图2中六个形状大小都相同的四边形围成一个圆的内接正六边形和一个小正六边形,若PQ所在的直线经过点M,PB=5cm,小正六边形的面积为cm2,则该圆的半径为_______________cm. 21.如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r1:r2=_________________。 22.如图,图1是由若干个相同的图形(图2)组成的美丽图案的一部分,图2中,图形的相关数据:半径OA=2cm,∠AOB=120°.则图2的周长为__________________-cm(结果保留π).
23.如图1,作∠BPC平分线的反向延长线PA,现要分别以∠APB,∠APC,∠BPC为内角作正多边形,且边长均为1,将作出的三个正多边形填充不同花纹后成为一个图案.例如,若以∠BPC为内角,可作出一个边长为1的正方形,此时∠BPC=90°,而=45是360°(多边形外角和)的,这样就恰好可作出两个边长均为1的正八边形,填充花纹后得到一个符合要求的图案,如图2所示.
(1)图2中的图案外轮廓周长是_____________;
(2)在所有符合要求的图案中选一个外轮廓周长最大的定为会标,则会标的外轮廓周长是____________.
T同步——弧长扇形面积计算
同步知识梳理
同步题型分析
图形变化
C专题——正多边形计算
专题导入
知识典例
圆大题计算
T能力——阴影部分面积
检测定位
1
同课章节目录
