人教版九年级上册 圆综合（无解析）

教师辅导讲义
学员编号： 年 级： 课 时 数： 学员姓名： 辅导科目： 学科教师：
授课类型 T同步(圆的性质) C专题(切线证明) T能力(最值)
授课日期及时段
教学内容
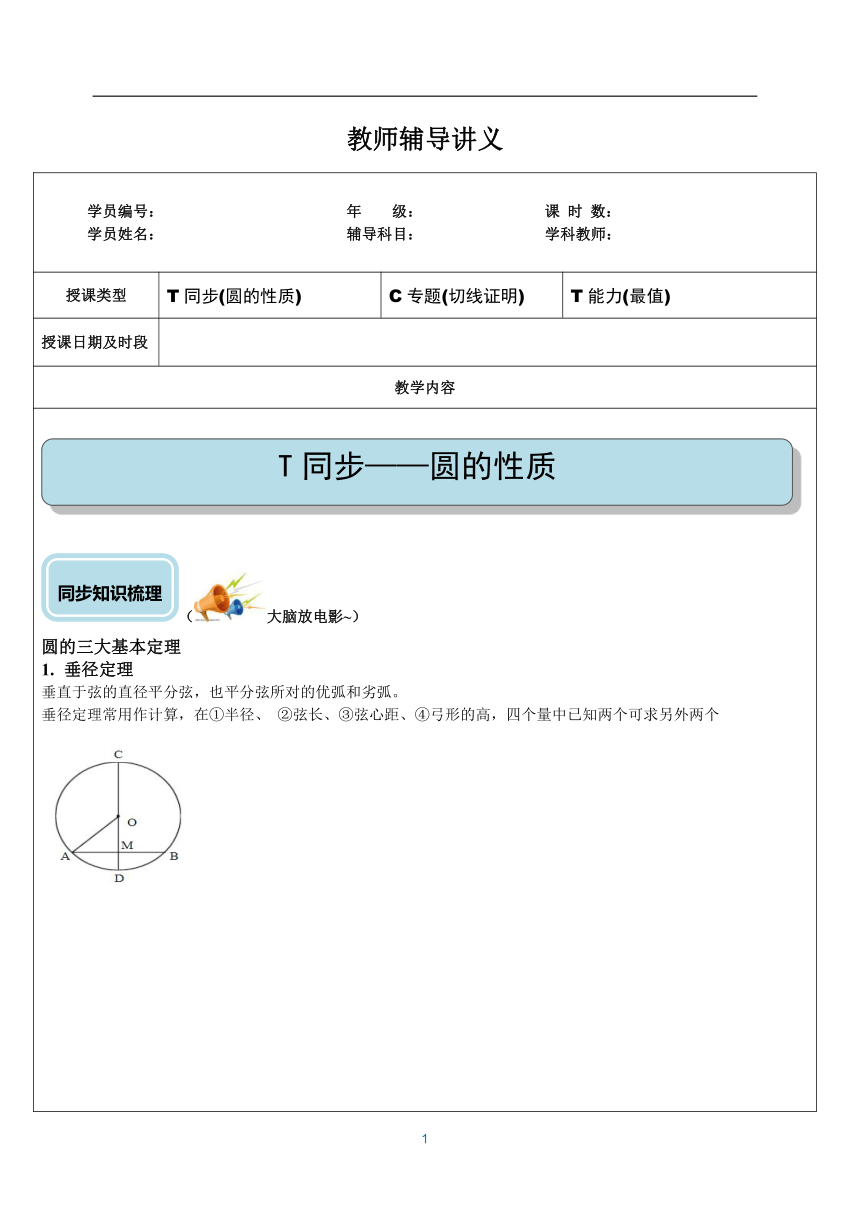
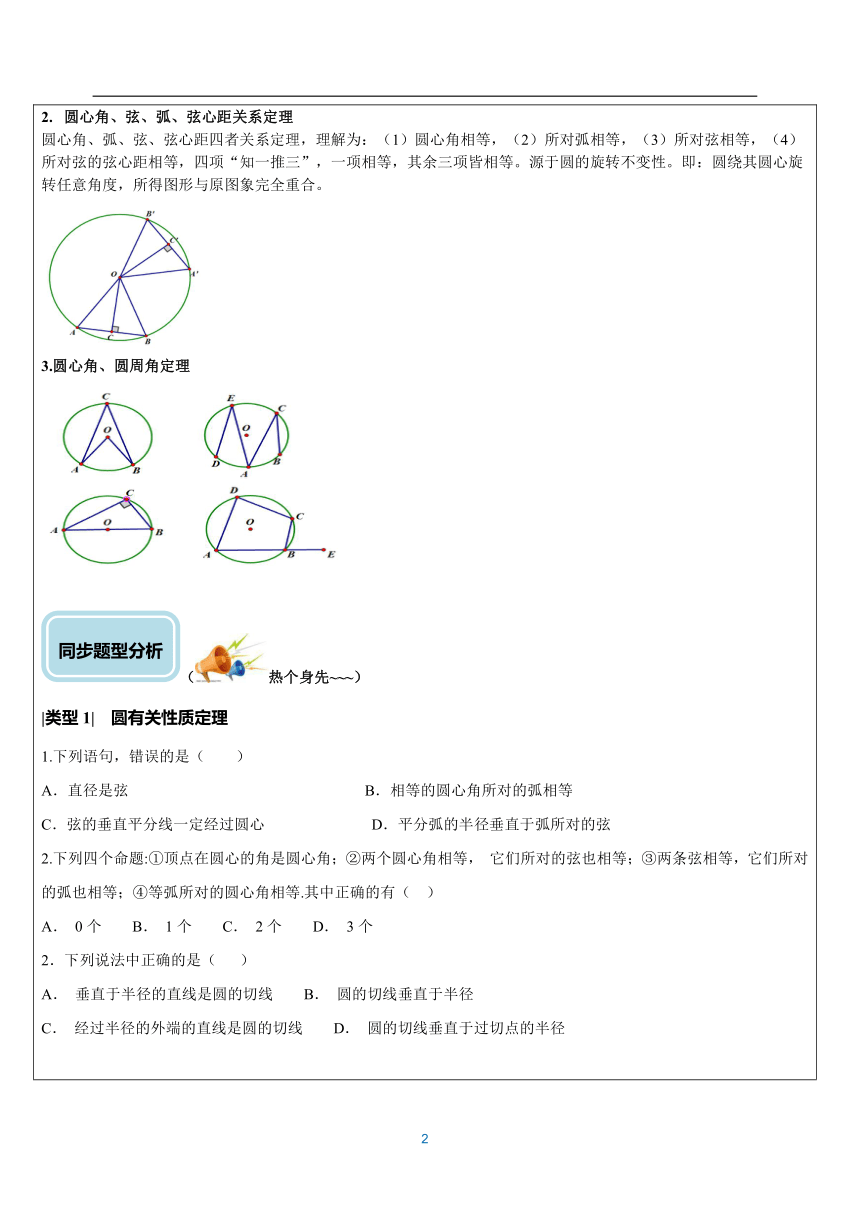
（大脑放电影~） 圆的三大基本定理 垂径定理垂直于弦的直径平分弦，也平分弦所对的优弧和劣弧。垂径定理常用作计算，在①半径、 ②弦长、③弦心距、④弓形的高，四个量中已知两个可求另外两个 圆心角、弦、弧、弦心距关系定理圆心角、弧、弦、弦心距四者关系定理，理解为：（1）圆心角相等，（2）所对弧相等，（3）所对弦相等，（4）所对弦的弦心距相等，四项“知一推三”，一项相等，其余三项皆相等。源于圆的旋转不变性。即：圆绕其圆心旋转任意角度，所得图形与原图象完全重合。3.圆心角、圆周角定理 （热个身先~~~） |类型1|　圆有关性质定理1.下列语句，错误的是（　　） A．直径是弦 B．相等的圆心角所对的弧相等 C．弦的垂直平分线一定经过圆心 D．平分弧的半径垂直于弧所对的弦 2.下列四个命题:①顶点在圆心的角是圆心角；②两个圆心角相等， 它们所对的弦也相等；③两条弦相等，它们所对的弧也相等；④等弧所对的圆心角相等.其中正确的有（ ） A． 0个 B． 1个 C． 2个 D． 3个 2．下列说法中正确的是（ ） A． 垂直于半径的直线是圆的切线 B． 圆的切线垂直于半径 C． 经过半径的外端的直线是圆的切线 D． 圆的切线垂直于过切点的半径 |类型1|　垂径定理⊙O的半径为5cm，弦AB//CD，且AB=8cm,CD=6cm,则AB与CD之间的距离为____ 2.点A，C为半径是3的圆周上两点，点B为弧AC的中点，以线段BA，BC为邻边作菱形ABCD，顶点D恰在该圆直径的三等分点上，则该菱形的边长为（ ） (　　) A．或2　　 　B．或2 C．或2 D．或23.如图，矩形ABCD的一边AD与⊙O相切于点E，点B在⊙O上、BC与⊙O相交于点F，AB=2，AD=7，FC=1，则⊙O的半径长为______ 4.如图，AB是⊙O的直径，弦CD交AB于点P，AP＝2，BP＝6，∠APC＝30°，则CD的长为_____. (　　)A．　B．2　　C．2　　D．8 5.如图，已知⊙O的半径为5，弦AB，CD所对的圆心角分别是∠AOB，COD，若∠AOB与∠COD互补，弦CD=6，则弦AB的长为（　　） A. 6 B. 8 C. 5 D. 5 6.如图，AB是半圆O的直径，C、D两点在半圆上，CE⊥AB于E，DF⊥AB于F，点P是AB上的一个动点，已知AB=10，CE=4，DF=3，则PC+PD的最小值是（　　） A．7 B．7 C．10 D．8 7.如图,在半径为13 cm的圆形铁片上切下一块高为8 cm的弓形铁片, 则弦AB的长为?(　　) ? A.10 cm　　B.16 cm　　C.24 cm　　D.26 cm 8.如图，△ABC内接于⊙O，AB为⊙O的直径，∠CAB＝60°，弦AD平分∠CAB，若AD＝6，则AC＝__________. 9.如图，⊙O的半径OA=4，弦BC经过OA的中点D，∠ADC=30°，则弦BC的长为（　　） A．7 B．2? 15 C．4? 3 D．2? 17 10.如图，点P是四边形ABCD外接圆⊙O上任意一点，且不与四边形顶点重合，AD是⊙O的直径，AB＝BC＝CD，连结PA，PB，PC.若PA＝a，则点A到PB和PC的距离之和AE＋AF＝__________. |类型2|　圆周角与圆心角 已知⊙O的半径为10，圆心O到弦AB的距离为5，则弦AB所对的圆周角的度数是_____2.如图，⊙O的直径AB与弦CD的延长线交于点E，若DE＝OB，∠AOC＝84°，则∠E等于(　　) A．42° B．28° C．21° D．20°3.如图，A，B，C是⊙O上的三个点，若∠BAC＝30°，BC＝2，则⊙O半径为(　　) A．2 B．2 C．4 D． 4.如图，AB是半圆⊙O的直径，△ABC的两边AC，BC分别交半圆于D，E，且E为BC的中点，已知∠BAC＝50°，则∠C＝(　　) A．55° B．60° C．65° D．70° 5.如图，在Rt△ABC中，∠ACB＝90°，∠A＝56°.以BC为直径的⊙O交AB于点D，E是⊙O上一点，且＝，连接OE.过点E作EF⊥OE，交AC的延长线于点F，则∠F的度数为(　　) A．92° B．108° C．112° D．124° 如图，四边形ABCD为⊙O的内接四边形，延长AB与DC相交于点G，AO⊥CD，垂足为E，连接BD，∠GBC＝50°，则∠DBC的度数为 (　　) A．50° B．60° C．80° D．85° 7.如图，四边形ABCD内接于⊙O，∠DAB=140°，连接OC，点P是半径OC上一点，则∠BPD不可能为（　　） A．40°B．60°C．80°D．90° 8.如图，四边形ABCD内接于⊙O，延长CO交圆于点E，连接BE．若∠A=100°，∠E=60°，则∠OCD的度数为（　　） A．30° B．50° C．60° D．80° 9.如图，已知在△ABC中，AB＝AC.以AB为直径作半圆O，交BC于点D.若∠BAC＝40°，则的度数是__________度. 10.如图，AB、CD是⊙O的两条弦，若∠AOB+∠C=180°，∠COD=∠A，则∠AOB=?________ （课堂精粹） 直线与圆的位置关系切线的判定和性质 (1)切线的判定定理：经过半径的外端并且________这条半径的直线是圆的切线． 一条直线只有满足：(1)经过半径的外端；(2)垂直于这条半径，这两个条件才是圆的切线，缺一不可． 【方法点拨】判定切线的方法有以下几种： (1)若直线与圆只有一个公共点，则这条直线是圆的切线； (2)连接圆心和圆与直线的公共点即为半径，再证它们互相垂直．简称“连半径证垂直”； (3)当直线与圆的公共点没有确定时，首先过圆心作出直线的垂线，再证垂线段的长等于半径．简称“作垂直证半径”． (2)切线的性质定理：圆的切线垂直于____________.切线证明常考题型1，如图：AB是⊙O的直径，点E、C是⊙O上的两点，基本结论： “AC平分∠BAE”； “AD⊥CD”； “DC是⊙O的切线” 三个论断中，知二推一。 2，如图：Rt⊿ABC中，∠ACB=90°。点O是AC上一点，以OC为半径作⊙O交AC于点E，基本结论： 在①BO平分∠CBA； ②BO∥DE； ③AB是⊙O的切线； ④BD=BC 四个论断中，知一推三。 3，如图：Rt⊿ABC中，∠ABC=90°,以AB为直径作⊙O交AC于D， 基本结论： DE与⊙O相切推出E是BC的中点 4，如图，⊿ABC中，AB=AC，以AB为直径作⊙O，交BC于点D，交AC于点F，基本结论： DE⊥AC 推出DE与⊙O相切 切线长及切线长定理 (1)切线长：从圆外一点引圆的两条切线，这一点到切点之间的______的长，叫做切线长； (2)切线长定理：从圆外一点可以引圆的两条切线，它们的切线长________，这一点和圆心的连线________两条切线的夹角． 三角形的外接圆与内切圆名称 图形 内、外心 性质 三角形 的外 接圆 三边垂直平分线的交点称为三角形的外心 三角形的外心到三角形__________的距离相等 三角形 的内 切圆 三条内角平分线的交点称为三角形的内心 三角形的内心到三角形________的距离相等 （ 画竹必先成竹于胸！） |类型1|　外接圆与内接圆1.如图，在中，，，,O是的内心，以O为圆心，r为半径的圆与线段AB有交点，则r的取值范围是（ ）A． B． C． D． 2．如图，在△ABC中，∠A＝60°，BC＝5 cm.能够将△ABC完全覆盖的最小圆形片的直径是______cm.3.如图，⊙O为锐角△ABC的外接圆，半径为5. (1)用尺规作图作出∠BAC的平分线，并标出它与劣弧BC的交点E(保留作图痕迹，不写作法)； (2)若(1)中的点E到弦BC的距离为3，求弦CE的长．4.如图，点A、B、C在同一条直线上，点D在直线AB外，过这四个点中的任意3个，能画的圆有（　　） A．1 个 B．2个 C．3个 D．4 个 5.如图所示，在边长为1的单位正方形组成的网格中，△ABC的顶点都在网格的交点上，则△ABC的外接圆半径R为（　　） A． B. C. D． 6.如图，点O为△ABC内一点，OA=OB=OC，且∠ABO=40°，则∠ACB的大小是（　　） A．40° B．50° C．60° D．70° 7.如图，点O为△ABC的外心，点I为△ABC的内心，若∠BOC=140°，则∠BIC的度数为（　　） A．110° B．125° C．130° D．140° 8.如图是一块△ABC余料，已知AB＝20 cm，BC＝7 cm，AC＝15 cm，现将余料裁剪成一个圆形材料，则该圆的最大面积是________cm2. 9.如图是由两个长方形组成的工件平面图（单位：mm），直线l是它的对称轴，若HG=60，AB=80，GF=50，CB=20，能完全覆盖这个平面图形的圆面的最小半径是__________mm． |类型2|　平面直角坐标系中的圆1在平面直角坐标系xOy中,以点O为圆心的圆分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣弧MN的长为π,直线y=-x+4与x轴、y轴分别交于点A,B.(1)求证:直线AB与☉O相切; (2)求图中所示的阴影部分的面积(结果用π表示). 2.AN是☉M的直径,NB∥x轴,AB交☉M于点C. (1)若点A,N,∠ABN=30°,求点B的坐标;(2)若D为线段NB的中点,求证:直线CD是☉M的切线. |类型3|　垂径定理与勾股定理联手1.如图,已知:AB是☉O的直径,点C在☉O上,CD是☉O的切线,AD⊥CD于点D.E是AB延长线上的一点,CE交☉O于点F,连接OC,AC. (1)求证:AC平分∠DAO. (2)若∠DAO=105°,∠E=30°. ①求∠OCE的度数; ②若☉O的半径为2,求线段EF的长. 2.在⊙O中，直径AB＝6，BC是弦，∠ABC＝30°，点P在BC上，点Q在⊙O上，且OP⊥PQ. (1)如图1，当PQ∥AB时，求PQ的长度； (2)如图2，当点P在BC上移动时，求PQ长的最大值 3．如图，BE是⊙O的直径，半径OA⊥弦BC，点D为垂足，连AE，EC． （1）若∠AEC=28°，求∠AOB的度数； （2）若∠BEA=∠B，BC=6，求⊙O的半径． |类型3|　与圆有关的图形的面积1.已知,如图,以等边三角形ABC的边BC为直径作☉O,分别交AB,AC于点D,E,过点D作DF⊥AC于点F. (1)求证:DF是☉O的切线;(2)若等边三角形ABC的边长为8,求由弧DE,DF,EF围成的阴影部分的面积. |类型4|　与圆的切线有关的问题1.在Rt△ABC中，∠C＝90°，BC＝3 cm，AC＝4 cm，以点C为圆心，以2.5 cm为半径画圆，则⊙C与直线AB的位置关系是( ) A．相交 　 B．相切 　　 C．相离 　　D．不能确定 2.如图，已知⊙O是以坐标原点O为圆心，1为半径的圆，∠AOB＝45°，点P在x轴上运动，若过点P且与OA平行的直线与⊙O有公共点，设点P(x，0)，则x的取值范围是____________________. 3.如图，∠APB＝30°，圆心在PB上的⊙O的半径为1cm，OP＝3cm，若⊙O沿BP方向平移，当⊙O与PA相切时，圆心O平移的距离为______cm． 4.如图，已知⊙O的直径AB＝12，弦AC＝10，D是的中点，过点D作DE⊥AC交AC的延长线于点E. (1)求证：DE是⊙O的切线； (2)求AE的长． 5.如图,已知?OABC的三个顶点A,B,C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB,AO的延 长线于点D,E,AE交半圆O于点F,连接CF.(1)判断直线DE与半圆O的位置关系,并说明理由. (2)①求证:CF=OC; ②若半圆O的半径为12,求阴影部分的周长. |类型5|　圆与四边形结合的问题1.正方形ABCD内接于☉O,如图T7-6所示,在劣弧AB上取一点E,连接DE,BE,过点D作DF∥BE交☉O于点F,连接BF,AF,且AF与DE相交于点G,求证:(1)四边形EBFD是矩形; (2)DG=BE. 2.如图，在△ABC中，AB=AC，以AB为直径的半圆交AC于点D，交BC于点E，延长AE至点F，使EF=AE，连接FB，FC.（1）求证：四边形ABFC是菱形.（2）若AD=7，BE=2，求半圆和菱形ABFC的面积. 3.如图，在四边形ABCD中，AD＝BC，∠B＝∠D，AD不平行于BC，过点C作CE∥AD交△ABC的外接圆O于点E，连接AE. (1)求证：四边形AECD为平行四边形； (2)连接CO，求证：CO平分∠BCE. 16.四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O. (1)利用图1,求证:四边形ABCD是菱形; (2)如图2,若CD的延长线与半圆相切于点F,已知直径AB=8. ①连接OE,求△OBE的面积; ②求的长. （比一比！） 动点运动轨迹——圆或圆弧型 动点轨迹为定圆，利用三点共线 方法指导：1．当动点的轨迹是定圆时，可利用“一定点与圆上的动点距离最大值为定点到圆心的距离与半径和，最小值为定点到圆心的距离与半径差”性质求解．2．试着观察“动点与其他定点连结的线段长是否为‘定值’或动点与两定点构成的角是否为直角”，这是常见判断动点轨迹是圆的条件。Ⅰ 动点到定点的距离不变，则点的轨迹是圆或圆弧；1.如图 1，在正方形 ABCD 中，边长为 2,点 E 是 AB 的中点，点 F 是 BC 边上任意一点，将△BEF 沿 EF 所在直线折叠得到△PEF，连接 AP，则 CP 的最小值________，AP 的最小值是_________. 【变式 1】在矩形 ABCD 中，已知 AB＝2cm，BC＝3cm，现有一根长为 2cm 的木棒 EF 紧贴着矩形的边（即两个端点始终落在矩形的边上），按逆时针方向滑动一周，则木棒 EF 的中点 P 在运动过程中所围成的图形的面积_______cm2. 【变式 2】如图，一根木棒 AB 长为 2a，斜靠在与地面 OM 垂直的墙壁 ON 上，与地面的倾斜角∠ABO＝60°，若木棒沿直线 NO 下滑，且 B 端沿直线 OM 向右滑行，则木棒中点 P 也随之运动，已知 A 端下滑到 A′时，AA′＝()a，则木棒中点 P 随之运动到 P′所经过的路线长_______________． 3．如图，在△ABC 中，∠ACB＝90°，AB＝5，BC＝3，P 是 AB 边上的动点（不与点 B 重合），将△BCP 沿 CP 所在的直线翻折，得到△B′CP，连接 B′A，则 B′A 长度的最小值是________． 如图，在□ABCD 中，∠BCD＝30°，BC＝4，CD＝3 3，M 是 AD 边的中点，N 是 AB 边上的一动点，将△AMN 沿 MN 所在直线翻折得到△A′MN，连接 A′C，则 A′C 长度的最小值是________． 5．如图，在四边形 ABCD 中，AB＝AC＝AD，若∠BAC＝25°，∠CAD＝75°， 则∠BDC＝_________°，∠DBC＝____________°． 定边对定角模型 定弦定角 当某条边与该边所对的角是定值时，该角的顶点的轨迹是圆弧． 见直角→找斜边（定长）→想直径→定外心→现“圆”形； 见定角→找对边（定长）→想周角→转心角→现“圆”形； 【一般解题步骤】①让主动点动一下，观察从动点的运动轨迹，发现从动点的运动轨迹是一段弧。 ②寻找不变的张角（这个时候一般是找出张角的补角，这个补角一般为45°、60°或者一个确定的三角函数的对角等） ③找张角所对的定弦，根据三点确定隐形圆。 ④确定圆心位置，计算隐形圆半径。 ⑤求出隐形圆圆心至所求线段定点的距离。 ⑥计算最值：在此基础上，根据点到圆的距离求最值（最大值或最小值）。 1．如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为_____． 2.如图，A(1，0)、B(3，0)，以AB为直径作⊙M，射线OF交⊙M于E、F两点，C为弧AB的中点，D为EF的中点．当射线OF绕O点旋转时，CD的最小值为________. 3.如图∠BAC=60°，半径长1的⊙O与∠BAC的两边相切，P为⊙O上一动点，以P为圆心，PA长为半径的⊙P交射线AB、AC于D、E两点，连接DE，则线段DE长度的最大值为（　　）3 B． 6 C． D． 4.如图，在平面直角坐标系中，已知点A（1，0），B（1﹣a，0），C（1+a，0）（a＞0），点P在以D（4，4）为圆心，1为半径的圆上运动，且始终满足∠BPC=90°，则a的最大值是______．5.如图，在等腰 Rt△ABC 中，AC＝BC＝，点 P 在以斜边 AB 为直径的半圆上，M 为 PC 的中点．当点 P 沿半圆从点 A 运动至点 B 时，点 M 运动的路径长是________． 6.如图，⊙O 的半径为 1，弦 AB＝1，点 P 为优弧 AB 上一动点，AC⊥AP 交直线 PB 于点 C，则△ABC 的最大面积是____________. 7.直线 y＝x＋4 分别与 x 轴、y 轴相交与点 M、N，边长为 2 的正方形OABC 一个顶点 O 在坐标系的原点，直线 AN 与 MC 相交与点 P，若正方形绕着点 O 旋转一周，则点 P 到点(0，2)长度的最小值是__________． 8.E、F是正方形ABCD的边AD上两个动点，满足AEDF?，连结CF交BD于点G，连结BE交AG于点H。若正方形的边长为2，则线段DH长度的最小值是?????????。 9.如图，边长为 3 的正方形 ABCD，两顶点 A、B 分别在平面直角坐标系的 x 轴、y 轴的正半轴上滑动，点 C 点 D 在第一象限，点 E 为正方形ABCD 的对称中心，连结 OE，则 OE 的长的最大值是____________． 10、AB是半圆O的直径，AB=10，弦AC长为8，点D是弧BC上一个动点，连接AD，作CP⊥AD，垂足为P，连接BP，则BP的最小值是_____。 11.已知以AB为直径的圆O，C为AB弧的中点，P为BC弧上任意一点CD⊥CP交AP于D，连结BD，若AB=6，则BD的最小值为_________ 12.如图，点P是正方形ABCD的对角线BD上的一个动点（不与B、D重合），连结AP，过点B作直线AP的垂线，垂足为H，连结DH，若正方形的边长为4，则线段DH长度的最小值是 ． 13.如图，在正方形ABCD中，AB=3，点E，F分别在CD，AD上，CE=DF，BE，CF相交于点G，连接DG .点E从点C运动到点D的过程中，DG的最小值为?? ? ? ? ? ?。
动点轨迹为其他曲线，构造三角形 方法指导：1．当动点轨迹不是“定线”或“定圆”时，不妨将此线段转化为一个三角形中，其中在该三角形中其他两条边位置不定但长度确定，则所求线段的最大值为其他两线段长之和，最小值为其他两线段长之差．2．在转化较难进行时需要借助于三角形的中位线及直角三角形斜边上的中线。 1、如图，在△ABC中，∠C=90°，AC=6，BC=3，点A、C分别在x轴、y轴上，当点A在x轴上运动时，点C随之在y轴上运动．在运动过程中，点B到原点的最大距离是( ) A．9 B．2 C．3 D．3＋3 2.如图，∠MON=90°，线段 AB 两端点分别在边 OM，ON 上，当 A 在边 OM 上运动时，B 随之在边 ON 上运动，AB=2 保持不变，以 AB 为边向外作等边△ABC，在运动过程中，四边形 AOBC 的面积的最大值是___________. 3、如图，平面直角坐标系中，将含 30°的三角尺的直角顶点 C 落在第二象限．其斜边两端点 A、B 分别落在 x 轴、y 轴上，且 AB=12cm. （1）若 OB=6cm． ①求点 C 的坐标； ②若点 A 向右滑动的距离与点 B 向上滑动的距离相等，求滑动的距离； （2）点 C 与点 O 的距离的最大值=___________cm． 4.如图，定长弦CD在以AB为直径的⊙O上滑动（点C、D与点A、B不重合），M是CD的中点，过点C作CP⊥AB于点P，若CD=3，AB=8，PM=l，则l的最大值 5.如图，在Rt△ABC中，∠ACB=90°，AC=4，BC=3，点D是平面内的一个动点，且AD=2，M为BD的中点，在D点运动过程中，线段CM长度的取值范围是 . 6.如图，△ABC中，CA=CB，AB=6，CD=4，E是高线CD的中点，以CE为半径作⊙C，G是⊙C上一个动点，P是AG中点，则DP的最大值为　 　． SHAPE \* MERGEFORMAT 2 双动点型 解决双动点问题的常用方法是转化为单动点问题，接着再用单动点的方法解决线段最值问题。有这样一类双动点，它是由某一动点所产生的，同样就可用“源动点”和“从动点”的分析方法来处理，现总结思考前三个步骤：(一)分析“源动点”的不变量．(二)分析“双动点”与“源动点”间关系．(三)转化为单动点问题。显然确定“双动点”与“源动点”间关系是实现转化的关键。 例1、△ABC中，∠C=90°，AB=10，AC:BC =3:4，过AB边上一点P作PE⊥AC于E，PF⊥BC于F，EF是垂足，则EF的最小值等于_____________。 2．如图,在Rt△ABC中，∠C=90°，BC=3，AC=4，D、E分别是AC、BC上的一点，且DE=3， 若以DE为直径的圆与斜边AB相交于M、N，则MN的最大值为（ ） B． C． D． 3.如图，在△ABC中，AB=10，AC=8，BC=6，以边AB的中点O为圆心，作半圆与AC相切，点P，Q分别是边BC和半圆上的动点，连接PQ，则PQ长的最大值与最小值的和是（　　） A．6 B．2+1 C．9 D． 利用勾股定理实现转化 1、如图，1.如图，⊙O的半径为2，点O到直线l的距离为3，点P是直线l上的一个动点，PQ切⊙O于点Q，则PQ的最小值为【 】 A． B． C．3 D．2 2.如右图，在Rt△AOB中，OA=OB=3，⊙O的半径为1，点P是AB边上的动点，过点P作⊙O的一条切线PQ（点Q为切点），则切线PQ的最小值为 。 3.如图，AB为⊙O的直径，C为半圆的中点，⊙C的半径为2，AB＝8，点P是直径AB上的一动点，PM与⊙C切于点M，则PM的取值范围为________________． 利用三角形边角关系转化 1.△ABC中，∠BAC=60°，∠ABC=45°，，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB，AC于E，F，连接EF，则线段EF长度的最小值为 . 2.如图，∠BAC=60°，半径长为1的圆O与∠BAC的两边相切，P为圆O上一动点，以P为圆心，PA长为半径的圆P交射线AB、AC于D、E两点，连接DE，则线段DE长度的最大值为( ). A．3 B．6 C． D． （化腐朽为神奇） 1．如图，在中， ． ， ． 是中线，点、同时从点出发，以相同的速度分别沿、方向移动，当点到达点时，运动停止，直线分别与、相交于、，则在点、移动过程中，点移动路线的长度为（ ）． A． B． C． D． 2．如图，以G（0，1）为圆心，半径为2的圆与x轴交于A、B两点，与y轴交于C、D两点，点E为⊙G上一动点，CF⊥AE于F．当点E从点B出发顺时针运动到点D时，点F所经过的路径长为（　　） A． B． C． D． 3．如图，⊙O的半径为2，AB、CD是互相垂直的两条直径，点P是⊙O上任意一点（P与A、B、C、D不重合），经过P作PM⊥AB于点M，PN⊥CD于点N，点Q是MN的中点，当点P沿着圆周转过45°时，点Q走过的路径长为（　　） A． B． C． D． 4．如图，在等腰Rt△ABC中，斜边AB=8，点P在以AC为直径的半圆上，M为PB的中点，当点P沿半圆从点A运动至点C时，点M运动的路径长是（　　） 2π B． π C． 2π D． 25.如图1，点P从扇形AOB的O点出发，沿O→A→B→0以1cm/s的速度匀速运动，图2是点P运动时，线段OP的长度y随时间x变化的关系图象，则扇形AOB中弦AB的长度为______cm． 6.如图，AB为⊙O的直径，且AB=4，点C在半圆上，OC⊥AB，垂足为点O，P为半圆上任意一点，过P点作PE⊥OC于点E，设△OPE的内心为M，连接OM、PM．（1）求∠OMP的度数；（2）当点P在半圆上从点B运动到点A时，求内心M所经过的路径长． （真金不怕火炼） 1.如图，⊙M的半径为2，圆心M的坐标为（3，4），点P是⊙M上的任意一点，PA⊥PB，且PA、PB与x轴分别交于A、B两点，若点A、点B关于原点O对称，则AB的最小值为（　　）A． 3 B． 4 C． 6 D． 82.如图，AB为⊙O的直径，C为⊙O上一点，其中AB=4，∠AOC=120°，P为⊙O上的动点，连AP，取AP中点Q，连CQ，则线段CQ的最大值为（　　） A.3 B． 1+ C． 1+3 D． 1+3.如图，Rt△ABC中，∠C=90°，AB=4，F是线段AC上一点，过点A的⊙F交AB于点D，E是线段BC上一点，且ED=EB，则EF的最小值为 （ ） A． 3 B． 2 C． D． 24.如图，点C是半圆AB上一动点，以BC为边作正方形BCDE使弧BC在正方形内，连OE，若AB=4cm，则OD的最大值为______cm．


T同步——圆的性质

同步知识梳理

同步题型分析

C专题——切线证明

专题导入

知识典例

T能力——最值

检测定位

路径最值

当堂检测









1