人教版数学八年级下册第十八章 平行四边形复习讲义(无解析)
文档属性
| 名称 | 人教版数学八年级下册第十八章 平行四边形复习讲义(无解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-29 23:32:04 | ||
图片预览




文档简介
教师辅导讲义
学员编号: 年 级: 课 时 数: 学员姓名: 辅导科目: 学科教师:
授课类型 T同步( 平行四边形 ) C专题( 特殊平行四边形 ) T能力
授课日期及时段
教学内容
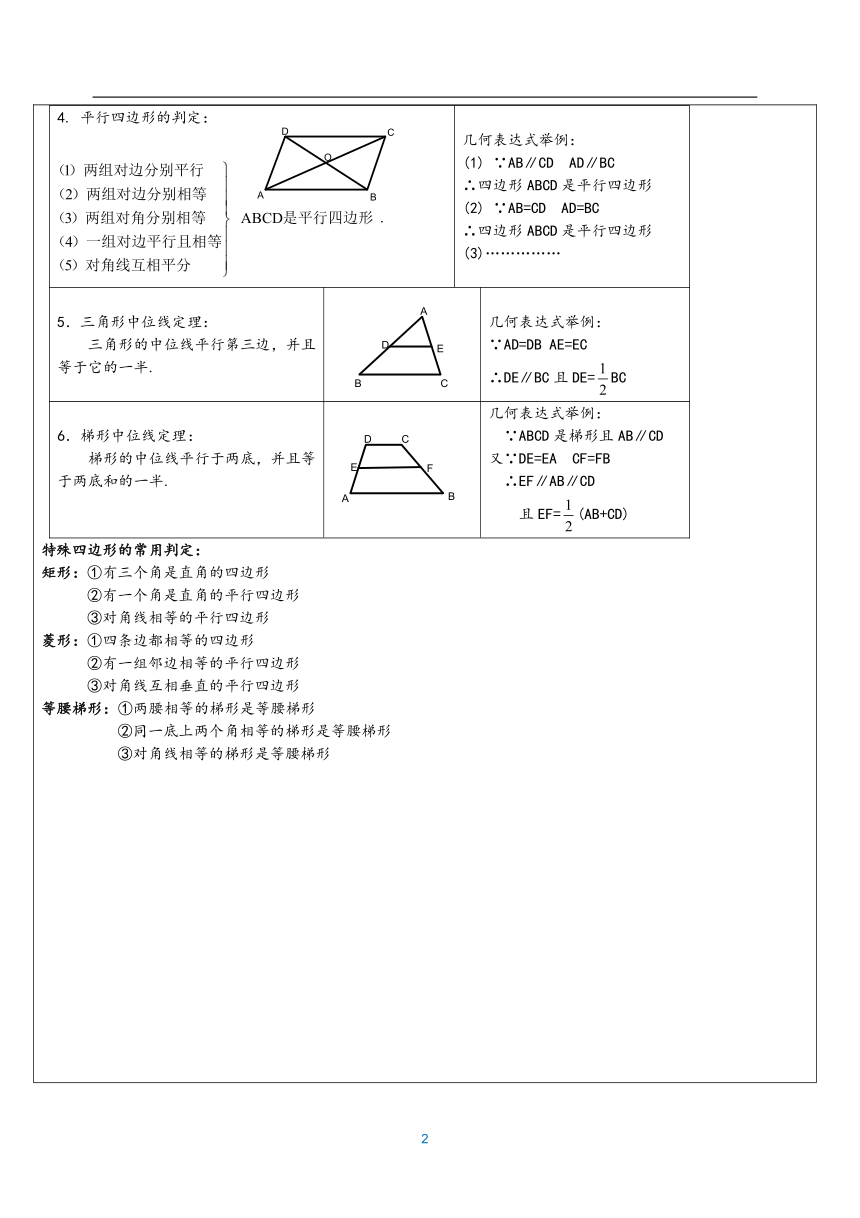
(大脑放电影~) 1.四边形的内角和与外角和定理: (1)四边形的内角和等于360°; (2)四边形的外角和等于360°. 几何表达式举例: (1) ∵∠A+∠B+∠C+∠D=360° ∴ …………… (2) ∵∠1+∠2+∠3+∠4=360° ∴ …………… 2.多边形的内角和与外角和定理: (1)n边形的内角和等于(n-2)180°; (2)任意多边形的外角和等于360°. 几何表达式举例:略 3.平行四边形的性质: 因为ABCD是平行四边形 几何表达式举例: (1) ∵ABCD是平行四边形 ∴AB∥CD AD∥BC (2) ∵ABCD是平行四边形 ∴AB=CD AD=BC (3) ∵ABCD是平行四边形 ∴∠ABC=∠ADC ∠DAB=∠BCD (4) ∵ABCD是平行四边形 ∴OA=OC OB=OD (5) ∵ABCD是平行四边形 ∴∠CDA+∠BAD=180° 平行四边形的判定: . 几何表达式举例: (1) ∵AB∥CD AD∥BC ∴四边形ABCD是平行四边形 (2) ∵AB=CD AD=BC ∴四边形ABCD是平行四边形 (3)…………… 5.三角形中位线定理: 三角形的中位线平行第三边,并且等于它的一半. 几何表达式举例: ∵AD=DB AE=EC ∴DE∥BC且DE=BC 6.梯形中位线定理: 梯形的中位线平行于两底,并且等于两底和的一半. 几何表达式举例: ∵ABCD是梯形且AB∥CD 又∵DE=EA CF=FB ∴EF∥AB∥CD 且EF=(AB+CD) 特殊四边形的常用判定: 矩形:①有三个角是直角的四边形 ②有一个角是直角的平行四边形 ③对角线相等的平行四边形菱形:①四条边都相等的四边形 ②有一组邻边相等的平行四边形 ③对角线互相垂直的平行四边形等腰梯形:①两腰相等的梯形是等腰梯形 ②同一底上两个角相等的梯形是等腰梯形 ③对角线相等的梯形是等腰梯形 (热个身先~~~) 平行四边形1、关于四边形 ABCD:①两组对边分别相等;②一组对边平行且相等;③一组对边平行 且另一组对边相等;④两条对角线相等. 以上四种条件中,可以判定四边形ABCD平行四边形的有( )个 A.1 个 B.2 个 C.3 个 D.4 个2、下列命题中,错误的是(? ?) 平行四边形的对角线互相平分?????????????????????????????菱形的对角线互相垂直平分矩形的对角线相等且互相垂直平分??????????????????????角平分线上的点到角两边的距离相等3、如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为________. 4、如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为( ) A.4? ???B.6?? ??C.8??? D.105、如图3,在 ABCD中,∠A的平分线交BC于点E.若AB=16cm,AD=25cm,则 EC=( ). 9cm B. 3cm C. 4cm D. 2cm6、如图,四边形ABCD是平行四边形,BE平分∠ABC,CF平分∠BCD,BE、CF交于点G.若使EF=AD,那么平行四边形ABCD应满足的条件是()
A.?∠ABC=60°???B.?AB:BC=1:4???C.?AB:BC=5:2????D.?AB:BC=5:8 7、如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E,F,G,H分别是AB,AC,CD,BD的中点,则四边形EFGH的周长是(??? ).
A.12 B.11 C.10 D.98、如图,在梯形ABCD中,∠ABC=90?,AE∥CD交BC于E,O是AC的中点,AB=,AD=2,BC=3,下列结论:①∠CAE=30?;②AC=2AB;③S△ADC=2S△ABE;④BO⊥CD,其中正确的是(?????)
A.?①②③?????B.?②③④???C.?①③④????D.?①②③④9、已知 a、b、c、d 为四边形的四边长,a、c 为对边,且满足, a2+b2+c2+d2=2ac+2bd,则这个四边形一定是 四边形。 10、如图,把一张平行四边形纸片ABCD沿BD对折,使点C落在点E处,BE与AD相交于点O , 若∠DBC=15°,则∠BOD= 。 11、如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为________.
如图所示,在四边形ABCD中,AB=CD,M、N、P分别是AD、BC、BD的中点,∠ABD=20°,∠BDC=70°,∠PMN的度数为______________.
13、如图,在平行四边形ABCD中,AD=2CD,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论①∠DCF=∠ECF;②EF=CF;③∠DFE=3∠AEF;④S△BEC<2S△CEF.中一定成立的是 .(请填序号)1、在平行四边形ABCD中, E,F分别是CD,AB边上的点,CE = 3DE, AF=BF,若平行四边形ABCD的面积为S,请分别求出⊿ADE, ⊿FBC的面积. 2、如图,已知平行四边形ABCD,点M,N分别在边AD和边BC上,点E,F在线段BD上,且AM=CN,DF=BE.求证: (1)∠DFM=∠BEN; (2)四边形MENF是平行四边形.3、如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿线段DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动.设运动的时间为t(秒).
(1)当t=2时,求△BPQ的面积;?
(2)若四边形ABQP为平行四边形,求运动时间t.
(3)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形? 矩形1、如图,在矩形ABCD中,AB=2BC,在CD上取一点E,使AE=AB,则∠EBC的度数为( ) A.30° B.15° C.45° D.不能确定2、已知:如图,在矩形ABCD中,BC=2,AE⊥BD,垂足为E,∠BAE=30°,那么△ECD的面积是( ) A. B. C. D.3、如图,在矩形ABCD中,AB=3,AD=4,点P在AB上,PE⊥AC于E,PF⊥BD于F,则PE+PF等于( ) A. B. C. D.4、如图,矩形ABCD的边AB=5cm,BC=4cm动点P从A点出发,在折线AD﹣DC﹣CB上以1cm/s 的速度向B点作匀速运动,则表示△ABP的面积S(cm)与运动时间t(s)之间的函数系的图象是( ) A. B. C. D. 5、如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为( ) A.1 B.1.2 C.1.3 D.1.56、在矩形ABCD中,AB=1,AD=,AF平分∠DAB,过C点作CEBD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为(? )
A.?1个??B.?2个????C.?3个???D.?4个1、如图,Rt△ABC中,∠C=90°,AC=3,BC=4,点P为AB边上任一点,过P分别作PE⊥AC于E,PF⊥BC于F,则线段EF的最小值是 .2、如图,在矩形ABCD中,AB=3,BC=4,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A恰落在∠BCD的平分线上时,则CA1的长为______. 3、如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B、C重合的一个动点,把△EBF沿EF折叠,点B落在B′处,若△CDB′恰为等腰三角形,则DB′的长为 .4、如图,一张长方形纸片 ABCD ,其长 AD 为 a ,宽 AB 为 b ( a > b ) ,在 BC 边上选取一点 M ,将△ ABM 沿 AM 翻折后 B 至 B ’ 的位置,若 B ’ 为长方形纸片 ABCD 的对称中心,则 的值是 __________ . 15、如图,矩形ABCD中,AB=8cm,BC=3cm,E是DC的中点,BF=FC,则四边形DBFE的面积为________cm2 .
16、如图,在矩形ABCD中,AC、BD相交于点O,AE平分∠BAD交BC于点E,若∠CAE=15°,∠BOE = 度。 17、如图,一副三角板拼在一起, O 为 AD 的中点, AB = a .将△ ABO 沿 BO 对折于△ A ’ BO , M 为 BC 上一动点,则 A ’ M 的最小值为 ________ .1、如图:矩形ABCD中,AB=2,BC=5,E、P分别在AD、BC上,且DE=BP=1. (1)判断△BEC的形状,并说明理由? (2)判断四边形EFPH是什么特殊四边形?并证明你的判断; (3)求四边形EFPH的面积. 2、已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC. ①求证:AD=CN; ②若∠BAN=90度,求证:四边形ADCN是矩形. 3、如图,四边形 ABCD 是矩形,△ PBC 和△ QCD 都是等边三角形,且点 P 在矩形上方,点 Q 在矩形内. 求证: PA = PQ . 4、如图,将矩形纸片 ABCD 沿对角线 AC 折叠使点 B 落到 B '的位置, AB '与 CD 交于点 E . ⑴试找出一个与△ AED 全等的三角形,并加以证明; ⑵若 AB = 8 , DE = 3 , P 为线段 AC 上的任意一点, PG ⊥ AE 于 G , PH ⊥ EC 于 H ,试求 PG + PH 的值,并说明理由.5、⑴观察与发现:讲矩形纸片 AOCB 折叠,使点 C 与点 A 重合,点 B 落在点 B '处 ( 如图 1) ,折痕为 EF .小明发现△ AEF 为等腰三角形,你同意吗?请说明理由.
⑵实验与应用:以点 O 为坐标原点,分别以矩形的边 OC 、 OA 为 x 轴、 y 轴建立如图所示的直角坐标系,若顶点 B 的坐标为 (9 , 3) ,请求出折痕 EF 的长及 EF 所在直线的函数关系式.5、如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F. (1)求证:EO=FO; (2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论. 6、如图 1 ,在△ ABC 中,点 P 为 BC 边中点,直线 a 绕顶点 A 旋转,若 B 、 P 在直线 a 的异侧, BM ⊥直线 a 于点 M , CN ⊥直线 a 于点 N ,连接 PM 、 PN ; ⑴延长 MP 交 CN 于点 E ( 如图 2) .①求证:△ BPM ≌△ CPE ;②求证: PM = PN ; ⑵若直线 a 绕点 A 旋转到图 3 的位置时,点 B 、 P 在直线 a 的同侧,其他条件不变,此时 PM = PN 还成立吗?若成立,请给予证明;若不成立,请说明理由; ⑶若直线 a 绕点 A 旋转到与 BC 边平行的位置时,其他条件不变.请直接判断四边形 MBCN 的形状及此时 PM = PN 还成立吗?不必说明理由. . 7、如图 1 ,在△ ABC 中, AB = BC , P 为 AB 边上一点,连接 CP ,以 PA 、 PC 为邻边作 □ APCD , AC 与 PD 相交于点 E ,已知∠ ABC =∠ AEP = α (0 °< α < 90 ° ) .
⑴求证:∠ EAP =∠ EPA ; ⑵ □ APCD 是否为矩形?请说明理由; ⑶如图 2 , F 为 BC 的中点,连接 FP ,将∠ AEP 绕点 E 顺时针旋转适当的角度,得到∠ MEN ( 点 M 、 N 分别是∠ MEN 的两边与 BA 、 FP 延长线的交点 ) .猜想线段 EM 与 EN 之间的数量关系,并证明你的结论. 菱形1、菱形具有而一般平行四边形不具有的性质是( ) A.对角相等 B.对角线相互平分 C.对边平行且相等 D.对角线相互垂直2、下列条件中,能判定四边形是菱形的是( ) A两条对角线相等 B两条对角线互相垂直 C两条对角线互相垂直平分 D两条对角线相等且相互垂直3、如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于( ) 3.5 B.4 C. 7 D. 14 4、如图,菱形花坛ABCD的边长为6m,∠A=120°,其中由两个正六边形组成的图形部分种花,则种花部分图形的周长为( ) A. 12m B. 20m C. 22m D. 24m 5、如图,菱形ABCD和菱形ECGF的边长分别为2和3,∠A=120°,则图中阴影部分的面积是( )A. B.2 C.3 D. 6、如图,菱形ABCD的周长为8cm,高AE长为cm,则对角线AC长和BD长之比为( ) (A)1:2 (B)1:3 (C)1: (D)1: 8、如图,在三角形ABC中,AB>AC,D、E分别是AB、AC上的点,△ADE沿线段DE翻折,使点A落在边BC上,记为A′.若四边形ADA′E是菱形,则下列说法正确的是( ) A. DE是△ABC的中位线 B. AA′是BC边上的中线 C. AA′是BC边上的高 D. AA′是△ABC的角平分线9、如图,边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,满AE+CF=a,△BEF的周长最小值是(??? )?????B.????C.???D.10、如图 , 在给定的一张平行四边形纸片上作一个菱形 . 甲、乙两人的作法如下 : 甲 : 连接 AC, 作 AC 的垂直平分线 MN 分别交 AD,AC,BC 于 M,O,N, 连接 AN,CM, 则四边形 ANCM 是菱形 . 乙 : 分别作∠ A, ∠ B 的平分线 AE,BF, 分别交 BC,AD 于 E,F, 连接 EF, 则四边形 ABEF 是菱形 . 根据两人的作法可判断 ( ) A. 甲 正确 , 乙错误 B. 乙正确 , 甲错误 C. 甲、乙均正确 D. 甲、乙均错误 11、如图,在菱形 ABCD 中, ∠ A = 110 ° , E , F 分别是边 AB 和 BC 的中点, EP ⊥ CD 于点 P ,则 ∠ FPC = ( ) A . 35 ° B . 45 ° C . 50 ° D . 5512、如图,在菱形ABCD中,∠A=60°,E、F分别是AB,AD的中点,DE、BF相交于点G,连接BD,CG.有下列结论:①∠BGD=120°;②BG+DG=CG;③△BDF≌△CGB;④S△ABD=AB其中正确的结论有( ) A.1个 B.2个 C.3个 D.4个13、如图,在菱形ABCD和菱形BEFG中,点A、B、E在同一直线上,P是线段DF的中点,连接PG,PC.若∠ABC=∠BEF=60°,则=( ) B. C. D. 1、如图 , 在四边形 ABCD 中 ,AC=BD=6,E,F,G,H 分别是 AB,BC,CD,DA 的中点 , 则 EG+FH = . 2、如图,四边形ABCD与四边形AECF都是菱形,点E,F在BD上,已知∠BAD=120°,∠EAF=30°,则= . 3、如图 , 在△ ABC 中 , ∠ ABC=90 ° ,BD 为 AC 的中线 , 过点 C 作 CE ⊥ BD 于点 E, 过点 A 作 BD 的平行线 , 交 CE 的延长线于点 F, 在 AF 的延长线上截取 FG=BD, 连接 BG,DF. 若 AG=13,CF=6, 则四边形 BDFG 的周长为 . 4、如图,边长为1的菱形ABCD中,∠DAB=60度.连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1,为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第n个菱形的边长为 。5、如图,菱形 的边长为 1 ,;作 于点 ,以 为一边,做第二个菱形 ,使;作于点 ,以为一边做第三个菱形,使 ; ……依此类推,这样做的第 个菱形 的边 的长是 . 1、如图1,纸片□ABCD中,AD=5,S□ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′ 的位置,拼成四边形AEE′D,则四边形AEE′D的形状为( ) A.平行四边形 B.菱形 C.矩形 D.正方形 (2)如图2,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,将它平移至△DE′F′ 的位置,拼成四边形AFF′D. ① 求证四边形AFF′D是菱形; ② 求四边形AFF′D两条对角线的长. 2、如图,菱形ABCD中,∠A=60°,连接BD,∠PBQ=60°,将∠PBQ绕点B任意旋转,交边AD,CD分别于点E、F(不与菱形的顶点重合),设菱形ABCD的边长为a(a为常数) (1)△ABD和△CBD都是 三角形; (2)判断△BEF的形状,并说明理由; (3)在运动过程中,四边形BEDF的面积是否变化,若不变,求出其面积的值(用a表示);若变化,请说明理由. (4)若a=3,设△DEF的周长为m,直接写出m的取值范围. 3、如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且∠EAG=∠BAD,连接EC,GD. (1)求证:EB=GD; (2)若∠DAB=60°,AB=2,AG=,求GD的长. 4、如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4?cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是ts(0
【拓展】如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F,求证:BE=DG.
【应用】如图③, 四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上,若AE=2ED,∠A=∠F,△EBC的面积为6,则菱形CEFG的面积为________.
四、正方形1、将n个边长都为1cm的正方形按如图所示的方法摆放,点A1,A2,…,An分别是正方形的中心,则n个这样的正方形重叠部分(阴影部分)的面积和为( ) A.cm2 B.cm2 C.cm2 D.cm2 2、如图,P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①△FPD是等腰直角三角形;②AP=EF;③AD=PD;④∠PFE=∠BAP.其中,所有正确的结论是( ??)
A.?①②?????B.?①④?????C.?①②④???D.?①③④3、已知,如图,在正方形ABCD中,O是对角线AC、BD的交点,过O作OE⊥OF,分别交AB、BC于点E、F,若AE=4,CF=3,则四边形OEBF的面积为 .如图,边长为a的正方形ABCD绕点A逆时针旋转30°得到正方形A′B′C′D′,图中阴影部分的面积为( ) A.a2 B.a2 C. (1﹣)a2 D. (1﹣)a2 4、如图,正方形ABCD中,E为DC边上一点,且DE=1,AE=EF,∠AEF=90°,则FC= (? ????)
A.????B.???????C.???????D.1 1、以△ABC的各边,在边BC的同侧分别作三个正方形.他们分别是正方形ABDI,BCFE,ACHG,试探究: (1)如图中四边形ADEG是什么四边形?并说明理由. (2)当△ABC满足什么条件时,四边形ADEG是矩形? (3)当△ABC满足什么条件时,四边形ADEG是正方形?2、已知:如图,在△ABC中,∠A>90°.以AB、AC为边分别在△ABC形外作正方形ABDE和正方形ACFG,EB、BC、CG、GE的中点分别是P、Q、M、N. (1)若连接BG、CE,求证:BG=CE. (2)试判断四边形PQMN为怎样的四边形,并证明你的结论. 3、如图,过△ ABC 的边 AB 、 AC 向外作正方形 ABDE 和正方形 ACFG , AH 是 BC 边上的高,延长 HA 交 EG 于点 I ,求证: I 是 EG 的中点. 4、如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF; (2)在图1中,若G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么? (3)根据你所学的知识,运用(1)、(2)解答中积累的经验,完成下列各题: ①如图2,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB的中点,且∠DCE=45°,求DE的长; 5、正方形ABCD中,E为直线AB上任意一点,DF⊥DE交直线BC的延长线于点F,直线EF、AC交于点H,连接DH (1)如图1当,点E在AB上时: ①判断线段DH与EF之间的位置关系与数量关系,并证明; ②AH-HC与AE之间的数量关系,并证明; ③求证:AB+AE=AH. (2)当点E在AB的反向延长线上时,如图2。 ①判断线段DH与EF之间的位置关系与数量关系,并证明; ②AH-HC与AE之间的数量关系,并证明; 3求证:AB+AE=AH (你都掌握了没有呢~~~) 1、下列命题中是假命题的是 ( ) A.平行四边形的对角线互相平分 B.对角线互相平分的四边形是平行四边形 C.菱形的对角线互相垂直 D.对角线互相垂直的四边形是菱形2、如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24cm,△OAB的周长是18cm,则EF等于(?? ) A.2cm????B.3cm?? C.4cm?? D.5cm3、如图,在 中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是 ( )A.5 B.10 C.15 D.204、如图,在矩形ABCD中,E为BC边的中点,∠AEC的平分线交AD边于点F,若AB=3,AD=8,则FD的长为(?? )
A.1 B.2 C.3 D.4 5、如图,在菱形ABCD中,AB=8,点E、F分别在AB、AD上,且AE=AF,过点E作EG∥AD交CD于点G,过点F作FH∥AB交BC于点H,EG与FH交于点O,当四边形AEOF与四边形CGOH的周长之差为12时,AE的值为( )A.6.5 B.6 C.5.5 D.56、如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连结EF,则△AEF的面积是( ) A. B. C. D. 7、如图,正方形ABCD的面积为9 . △ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使 PD+PE的和最小,则这个最小值为(??? ).
A.?3?????????????????????????????????????B.?????????????????????????????????????C.??????????????????????????????????????D.?8、如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间________秒时,以点P,Q,E,D为顶点的四边形是平行四边形. 9、如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则折痕EF的长为________. 10、已知直角坐标系中,四边形OABC是矩形,点A(10,0),点C(0,4),点D是OA的中点,点P是BC边上的一个动点,当△POD是等腰三角形时,点P的坐标为 .11、如图,在矩形ABCD中,AB=5,BC=7,点E为BC上一动点,把△ABE沿AE折叠,当点B的对应点B′落在∠ADC的角平分线上时,则点B′到BC的距离为_______.12、在矩形ABCD中,AC=8 , BC=4 ,若点M、N分别是线段AC、AB上的两个动点 ,则BM+MN的最小值为_____。13、如图,在矩形 ABCD 中,已知 AD = 12 , AB = 5 , P 是 AD 边上任意一点, PE ⊥ BD , PF ⊥ AC , E 、 F 分别是垂足,则 PE + PF = __________ .14、如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF. 求证:四边形BECF是平行四边形. 15、如图,在□ABCD中,AC、BD交于点O,EF过点O,分别交CB、AD的延长线于点E、F.。求证:AE=CF16、如图4-27,在□ABCD中,AC,BD交于O点,AE⊥BD于E,CG⊥BD于G,BH⊥ AC于H,DF⊥AC于F.求证:四边形EFGH为平行四边形.已知:如图,矩形ABCD中,DE交BC于E,且DE=AD,AF⊥DE于F. 求证:AB=AF.
18、如图,矩形ABCD中,AB=4cm,BC=8cm,动点M从点D出发,按折线DCBAD方向以2cm/s的速度运动,动点N从点D出发,按折线DABCD方向以1cm/s的速度运动. (1)若动点M、N同时出发,经过几秒钟两点相遇? (2)若点E在线段BC上,且BE=3cm,若动点M、N同时出发,相遇时停止运动,经过几秒钟,点A、E、M、N组成平行四边形?19、如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2. (1)求证:△BDE≌△BCF; (2)判断△BEF的形状,并说明理由; (3)设△BEF的面积为S,求S的取值范围. 20、如图,在正方形中,分别是边上的点,满足的周长等于正方形的周长的一半,分别与对角线交于,试问线段、、能否构成三角形的三边长?若能,指出三角形的形状,并给出证明;若不能,请说明理由。 21、如图,四边形ABCD中,AB=AD,CB=CD,AB∥CD.
(1)求证:四边形ABCD是菱形.
(2)当△ABD满足什么条件时,四边形ABCD是正方形.(直接写出一个符合要求的条件)
(3)对角线AC和BD交于点O,∠ADC=120°,AC=8,P为对角线AC上的一个动点,连接DP,将DP绕点D逆时针方向旋转120°得到线段DP1,直接写出AP1的取值范围.
22、如图 1 , P 是线段 AB 上的一点,在 AB 的同侧作△ APC 和△ BPD ,使 PC = PA , PD = PB ,∠ APC =∠ BPD ,连接 CD ,点 E 、 F 、 G 、 H 分别是 AC 、 AB 、 BD 、 CD 的中点,顺次连接 E 、 F 、 G 、 H . ⑴猜想四边形 EFGH 的形状,直接回答,不必说明理由;、 ⑵当点 P 在线段 AB 的上方时,如图 2 ,在△ APB 的外部作△ APC 和△ BPD ,其他条件不变,⑴中的结论还成立吗?说明理由. ⑶如果⑵中,∠ APC =∠ BPD = 90 °,其他条件不变,先补全图 3 ,再判定四边形 EFGH 的形状,并说明理由. ( 画竹必先成竹于胸!) 1、如图,已知正方形 ABCD 的边长为 4 ,对称中心为点 P ,点 F 为 BC 边上一个动点,点 E 在 AB 边上,且满足条件 ∠ EPF =45° ,图中两块阴影部分图形关于直线 AC 成轴对称 ,设它们的面积和为 S . ( 1 )求证: ∠ APE = ∠ CFP ; ( 2 )设四边形 CMPF 的面积为 S 2 , CF = x , . 求 y 关于 x 的函数解析式和自变量 x 的取值范围,并求出 y 的最大值; ② 当图中两块阴影部分图形关于点 P 成中心对称时,求 y 的值. 2、如图1,正方形ABOC中,AF⊥AE交OC的延长线于F,E在线段OB上运动,∠OEF的平分线交AO于D.
(1)如图1,求证:∠AEF=45°;
(2)过D作DH⊥EF于H,试探究DH、AC、EF之间的数量关系并说明理由.
(3)在第(2)题的条件下,如图点K为ED的延长线上一点,且∠EKO=∠EFO,KG⊥OC于H,EF=13,DH=2,直接写出OG的长. 3、已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)求证:EG=CG;
(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG. 问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论(均不要求证明).
4、(1)已知:如图1,在正方形ABCD中,E是BC的中点,F为DC上一点,且∠1=∠2,求证:AF=BC+FC;
(2)已知:如图2,把三角尺的直角顶点落在矩形ABCD的对角线交点P处,若旋转三角尺时,它的两条直角边与矩形的两边BC、CD分别相交于M、N,试证:MN2=BM2+DN2.
5、 如图,正方形OEFG绕着正方形ABCD的对角线的交点O旋转,边OE、OG分别交边AD、AB于点M、N.
(1)求证:OM=ON;
(2)设正方形OEFG的对角线OF与边AB相交于点P,连接PM.若正方形ABCD的边长为12,且PM=5,试求AM的长. 6、如图,正方形ABCD的顶点A、B分别在x轴和y轴上,DC的延长线交y轴于E,CB的延长线交x的负半轴于F.
(1)求证:△ABF≌△BCE;
(2)连接EF,若EF=5,OF=1,OB=2,求正方形ABCD的边长;
(3)在(2)的条件下,动点P从点A出发沿x轴正方向向右移动,当AP为多少时,△PAD为等腰三角形?
7、已知E、F分别为正方形ABCD的边BC、CD上的点,且∠EAF=45°.
(1)如图①求证:BE+DF=EF;
(2)连接BD分别交AE、AF于M、N,
①如图②,若AB=6,BM=3,求MN.
②如图③,若EF∥BD,求证:MN=CE.
8、在正方形ABCD中,点E在边BC上,连接DE,交对角线AC于点F,连接BF.
(1)求证:BF=DF;
(2)如图2,对角线BD与AC交于点O,过点F作直线FG⊥DF,交射线BC于点G,交BD于点N,求证:∠ONF=∠OBF+2∠FBC;
(3)如图3,在(2)的条件下,过点G作GM⊥FG,交射线BF于点M,如果FN=2,BM=9,求线段OF的长. 9、如图,在正方形ABCD中,AB=4,P是对角线AC上一个动点,连接PD,过点P向P点右侧作PD的垂线PQ交射线BC于点Q,连接DQ.
(1)如图1,PM⊥BC,PN⊥CD,求证:DP=PQ;
(2)如图2,连接AQ,在点P从点A向点C运动过程中,求△AQD周长的最小值.
(3)直接写出当PC为何值时,△PQC是等腰三角形.
10、如图,已知正方形ABCD的边长为4,点P是AB边上的一个动点,连接CP,过点P作PC的垂线交AD于点E,以PE为边作正方形PEFG,顶点G在线段PC上.对角线EG、FP相交于点O.
(1)若AP=3,求AE的长;
(2)连接AC,判断点O是否在AC上,并说明理由;
(3)在点P从点A到点B的运动过程中,正方形PEFG也随之运动,求DE的最小值. (比一比!) 1、(拓展创新)一位女士想买一条方纱巾,有一天她在商店里看到一块漂亮的纱巾,非常想买,但她拿起来看时感觉纱巾不太方,商店老板看她犹豫不决的样子,马上过来拉起一组对角,让女士看另一组对角是否对齐,如图所示,女士还有些疑惑,老板又拉起另一组对角让女士检验,女士终于买下这块纱巾,你认为女士买的这块纱巾是正方形的吗?当时采用什么方法可以检验出来? 2、如图,四边形ABCD是矩形纸片,AB=2,对折矩形纸片ABCD,使AD与BC重合,折痕为MN,展平后再过点B折叠矩形纸片,使点A落在MN上的点G处,折痕BE与MN相交于点H;再次展平,连接BG,EG,延长EG交BC于点F.有如下结论: ①EG=FG;②∠ABG=60°;③AE=1;④△BEF是等边三角形;其中正确结论的序号是________.
3、如图1,正方形纸片ABCD的边长为2,翻折∠B、∠D,使两个直角的顶点重合于对角线BD上一点P,EF、GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
①当x=1时,点P是正方形ABCD的中心;
②当x= 时,EF+GH>AC;
③当0<x<2时,六边形AEFCHG面积的最大值是 ;
④当0<x<2时,六边形AEFCHG周长的值不变.
其中正确的是________(写出所有正确判断的序号). 4、若一个矩形的一边是另一边的两倍,则称这个矩形为方形,如图 1 ,矩形 ABCD 中, BC=2AB ,则称 ABCD 为方形. ( 1 )设 a , b 是方形的一组邻边长,写出 a , b 的值(一组即可). ( 2 )在 △ ABC 中,将 AB , AC 分别五等分,连结两边对应的等分点,以这些连结为一边作矩形,使这些矩形的边 , , , 的对边分别在 , , , BC 上,如图 2 所示. ① 若 BC=25 , BC 边上的高为 20 ,判断以 B 1 C 1 为一边的矩形是不是方形?为什么? ② 若以为一边的矩形为方形,求 BC 与 BC 边上的高之比. 5、如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,
(1)求∠EAF的度数; (2)在图①中,连结BD分别交AE、AF于点M、N,将△ADN绕点A顺时针旋转90°至△ABH位置,连结MH,得到图②.求证:MN2=MB2+ ND2; (3)在图②中,若AG=12, BM= ,直接写出MN的值. 6、在平面直角坐标系中,O是坐标原点,矩形OABC的位置如图所示,点A,C的坐标分别为(10,0),(0,8).点P是y轴上的一个动点,将△OAP沿AP翻折得到△O′AP,直线BC与直线O′P交于点E,与直线O′A交于点F. (1)当点P在y轴正半轴,且∠OAP=30?时,求点O′的坐标,并判断点O′落在矩形OABC的内部还是外部。 (2)当O′落在直线BC上时,求直线O′A的解析式。 (3)在点P的运动过程中,是否存在某一时刻,使得线段CF与线段OP的长度相等?若存在,请求出点P的坐标;若不存在,请说明理由。 7、如图,AC 为正方形 ABCD 的对角线,点 E 为 DC 边上一点(不与 C、D 重合),连接BE,以 E 为旋转中心,将线段 EB 逆时针旋转 90°,得到线段 EF,连接 DF. (1)请在图中补全图形. (2)求证:AC∥ DF. (3)探索线段 ED、DF、AC 的数量关系,并加以证明.
T同步——平行四边形同步训练
同步知识梳理
同步题型分析
E
F
C
D
B
A
B′
课堂达标检测
N
F
M
E
B
D
A
C
C专题
知识典例
T能力
检测定位
1
