人教版数学八年级下册第十九章 一次函数复习讲义(无答案)
文档属性
| 名称 | 人教版数学八年级下册第十九章 一次函数复习讲义(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 626.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-29 00:00:00 | ||
图片预览





文档简介
教师辅导讲义
学员编号: 年 级: 课 时 数: 学员姓名: 辅导科目: 学科教师:
授课类型 T同步( 一次函数图像与性质 ) C专题( 一次函数实际应用 ) T能力
授课日期及时段
教学内容
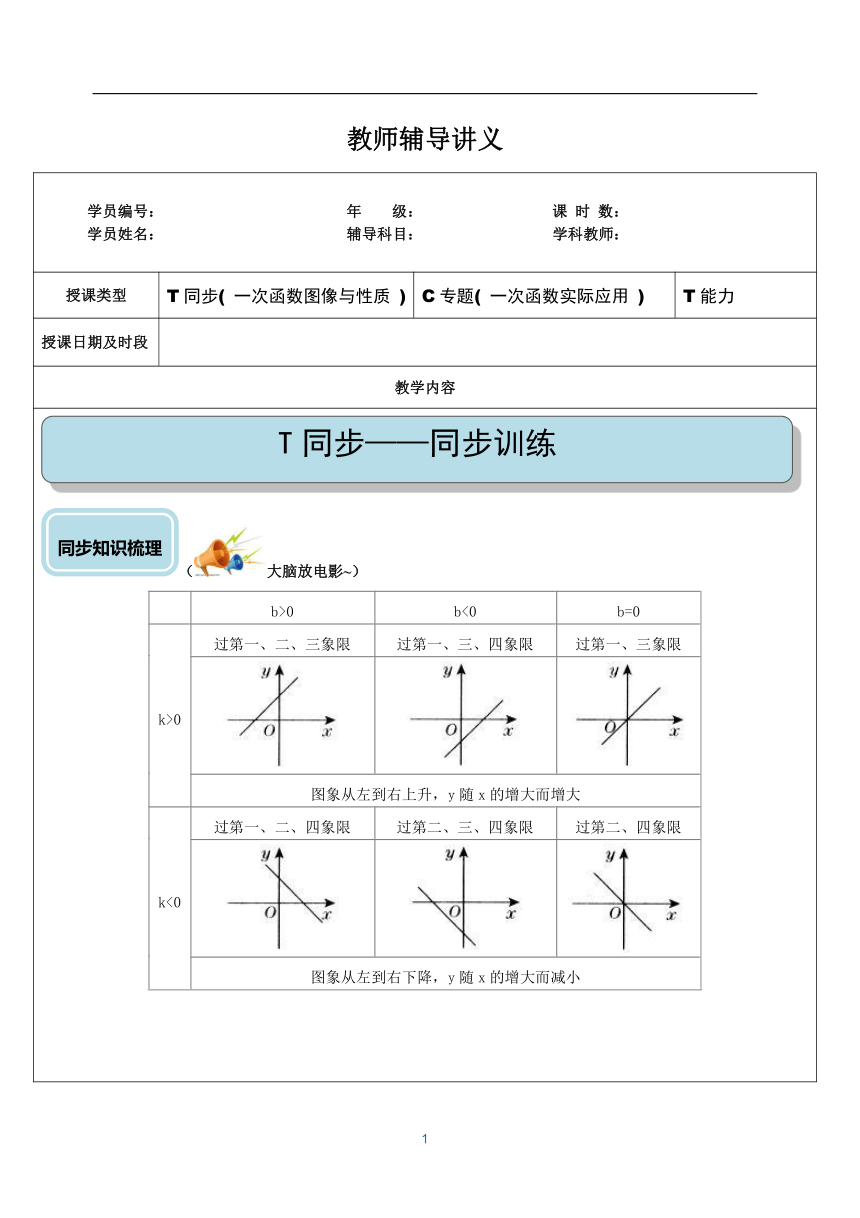
(大脑放电影~) b>0 b<0 b=0 k>0 过第一、二、三象限 过第一、三、四象限 过第一、三象限 图象从左到右上升,y随x的增大而增大 k<0 过第一、二、四象限 过第二、三、四象限 过第二、四象限 图象从左到右下降,y随x的增大而减小 (热个身先~~~) 1、函数y=中的自变量x的取值范围是( ) B. C. D.2、若直线经过点和,且,则的值可以是( )A.3 B.4 C.5 D.63、若点在一次函数的图像上,且,则的取值范围为( )A. B. C. D.4、当k<0时,一次函数y=kx﹣k的图象不经过( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限5、在同一平面直角坐标系中,直线与直线的交点不可能在( ) A.第一象限 B.第二象限 C. 第三象限 D.第四象限 6、一次函数的图象经过点,且与轴、轴分别交于点、,则的面积是( ) A. B. C.4 D.87、 若点M(-7,m)、N(-8,n)都是函数y=-(k2+2k+4)x+1(k为常数)的图象上,则m和n的大小关系是( ) A.m>n B.m<n C.m=n D.不能确定8、已知一次函数的图象与轴的负半轴相交,且函数值随自变量的增大而减小,则下列结论正确的是( ) A. B. C. D. 9、一次函数是常数,)的图象,如图所示,则不等式的解集是 ( ) A. B. C. D. 如图,函数与的图象相交于点,则关于的不等式的解集是( ) B. C. D.11、根据如图所示的程序计算函数y的值,若输入x的值是7,则输出y的值是-2,若输入x的值是-8,则输出y的值是( )
A.5 B.10 C.19 D.21 1、当m=_____________时,函数y=-(m-2)x+(m-4)是一次函数。2、设点(﹣1,m)和点(,n)是直线(0<k<1)上的两个点,则m、n的大小关系为 .3、已知点P(1,2)关于x轴的对称点为P′,且P′在直线y=kx+3上,把直线y=kx+3的图象向上平移2个单位,所得的直线解析式为 .4、把一次函数y=kx+1的图象向上平移1个单位,再向右平移3个单位后所得直线正好经过点(5,3),则该一次函数表达式为:________. 5、已知直线y1=x,y2= x+1,y3=﹣ x+5的图象如图所示,若无论x取何值,y总取y1 , y2 , y3中的最小值,则y的最大值为________. 6、如图,已知函数y=x﹣2和y=﹣2x+1的图象交于点P(1,﹣1),根据图象可得方程组 ?的解是________. 7、一次函数y=2x+6的图象如图所示,则不等式2x+6>0的解集是________,当y≤3时,x的取值范围是________. 如图,直线y=kx+b与y=x交于A(3,1)与x轴交于B(6,0),则不等式组的解集为________. 1、已知y+a与x+b(a,b为是常数)成正比例. (1)y是x的一次函数吗?请说明理由; (2)在什么条件下,y是x的正比例函数? 2.已知一次函数y=(m﹣2)x+2m+3,
(1)当m为何值时,y随x的增大而增大?
(2)当m为何值时,图象经过第一、二、四象限? 3、求图象经过点(2,-1),且与直线y=2x+1平行的一次函数的表达式. 4、如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b). (1)求b,m的值; (2)垂直于x轴的直线x=a与直线l1,l2分别交于点C,D,若线段CD长为2,求a的值. 5、如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b).①求b的值;②不解关于x , y的方程组 ,请你直接写出它的解;
③直线l3:y=nx+m是否也经过点P?请说明理由.
6、如图,在直角坐标系中,矩形OABC的顶点B的坐标为(15,6),直线y=x+b恰好将矩形OABC分为面积相等的两部分,试求b的值。 1、如图①,在矩形ABCD中,AB<AD,对角线AC,BD相交于点O,动点P由点A出发,沿AB→BC→CD向点D运动.设点P的运动路程为x,△AOP的面积为y,y与x的函数关系图象如图②所示,则AD边的长为( )
A.3 B.4 C.5 D.6 2、如图,在矩形ABCD中,AB=2,BC=3,动点P沿折线BCD从点B开始运动到点D.设运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是( )B.C.D. 3、均匀的向一个容器内注水,在注满水的过程中,水面的高度h与时间t的函数关系如图所示,则该容器是下列四个中的( )A. B. C. D.4、如图1,将正方形ABCD按图1所示置于平面直角坐标系中,AD边与x轴重合顶点B,C位于轴上方,将直线l:y=x-3沿x轴向左以每秒1个单位长度的速度平移,在平移的过程中,该直线被正方形ABCD的边所截得的线段长为m,平移的时间为t秒,m与t的函数图象如图2所示,则a,b的值分别是( )
A. B. C. D.5、小明家、食堂,图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家,如图反映了这个过程中,小明离家的距离y(km)与时间x(min)之间的对应关系,根据图象,下列说法正确的是( )A.小明吃早餐用了25min B.食堂到图书馆的距离为0.6km C.小明读报用了30min D.小明从图书馆回家的速度为0.8km/min 6、小明和小华是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公共汽车到了学校.如图是他们从家到学校已走的路程s(米)和所用时间t(分钟)的关系图.则下列说法中正确的是( )
①小明家和学校距离1200米;
?②小华乘坐公共汽车的速度是240米/分;
③小华乘坐公共汽车后7:50与小明相遇;
④小华的出发时间不变,当小华由乘公共汽车变为跑步,且跑步的速度是100米/分时,他们可以同时到达学校.A.①③④B.①②③C.①②④D.①②③④ 7、张老师出门散步时离家的距离y与时间x之间的函数图象如图所示,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是( )A.B.C.D. 8、汽车的“燃油效率”是指汽车每消耗 1 升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( ) A.以相同速度行驶相同路程,甲车消耗汽油最多 B.以 10 km/h 的速度行驶时,消耗 1 升汽油,甲车最少行驶 5 千米 C.以低于 80 km/h 的速度行驶时,行驶相同路程,丙车消耗汽油最少 D.以高于 80 km/h 的速度行驶时,行驶相同路程,丙车比乙车省油 1、一慢车和一快车沿相同路线从A地到B地,所行的路程与时间图象如图,则慢车比快车早出发________小时,快车追上慢车行驶了________千米,快车比慢车早________小时到达B地.
2、如图,已知直线l:与x轴交于点A,与y轴交于点B,将△AOB沿直线l折叠,点O落在点C处,则直线CA的表达式为__________________. 3、如图,矩形ABCD的边AB在x轴上,AB的中点与原点O重合,AB=2,AD=1,过定点Q(0,2)和动点P(a,0)的直线与矩形ABCD的边有公共点. (1)a的取值范围是________________; (2)若设直线PQ为y=kx+2(k≠0),则此时k的取值范围是________________.4、如图,已知直线l1:与直线l2:y=-2x+16相交于点C,直线l1,l2分别交x轴于A,B两点,矩形DEFG的顶点D,E分别在l1,l2上,顶点F,G都在x轴上,且点G与点B重合,那么S矩形DEFG:S△ABC =_________. 5、旅客乘车按规定可以随身携带一定重量的行李,如果超过规定,则需要购买行李票,设行李费y(元)与行李重量x(千克)的关系如图,根据图象回答下列问题: (1)行李重量在________千克以内,不必交费; (2)当行李重量60千克时,交费________元; (3)当行李重量________千克时,交费10元; (4)行李重量每增加1千克,多交________元; (5)y = 。( y与x之间的关系式) 6、某市的出租车收费y(元)与路程x(千米)之间的函数关系如图所示:
(1)图中AB段的意义是________. (2)当x>2时,y与x的函数关系式为________. (3)张先生打算乘出租车从甲地去丙地,但需途径乙地办点事,已知甲地到乙地的路程为1km,乙地至丙地的路程是3km,现有两种打车方案:
方案一:先打车从甲地到乙地,办完事后,再打另一部出租车去丙地
方案二:先打车从甲地到乙地,让出租车司机等候,办完事后,继续乘该车去丙地(出租车等候期间,张先生每分钟另付0.2元,假设计价器不变)张先生应选择哪种方案较为合算?试说明理由。 7、某地区为了鼓励市民节约用水,计划实行生活用水按阶梯式水价计费,每月用水量不超过10吨(含10吨)时,每吨按基础价收费;每月用水量超过10吨时,超过的部分每吨按调节价收费.例如,第一个月用水16吨,需交水费17.8元,第二个月用水20吨,需交水费23元. (1)求每吨水的基础价和调节价; (2)设每月用水量为n吨,应交水费为m元,写出m与n之间的函数解析式; (3)若某月用水12吨,应交水费多少元? 8、某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格. 空调彩电 进价(元/台)54003500 售价(元/台)61003900 设商场计划购进空调x台,空调和彩电全部销售后商场获得的利润为y元. (1)试写出y与x的函数关系式; (2)商场有哪几种进货方案可供选择? (3)选择哪种进货方案,商场获利最大?最大利润是多少元? 一次函数动点问题:1、如图,已知正方形ABCD的顶点A(1,1),B(3,1),直线y=2x+b交边AB于点E,交边CD于点F,则直线y=2x+b在y轴上的截距b的变化范围是____________. 2、如图,直线y=﹣x+4与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外). (1)求点P运动的速度是多少? (2)当t为多少秒时,矩形PEFQ为正方形? (3)当t为多少秒时,矩形PEFQ的面积S最大?并求出最大值. 3、如图,直线与x轴交于点A,与直线交于点P. (1)求点P的坐标. (2)求△OPA的面积. (3)动点E从原点O出发,以每秒1个单位的速度沿OA方向向终点A运动,过点E作EF⊥x轴交线段OP或线段PA于点F,FB⊥y轴于点B.设运动时间为t秒,矩形OEFB与△OPA重叠部分的面积为S,求S与t之间的函数关系式. 4、如图,直线l的解析式为y=-x+4,它与x轴、y轴分别交于A,B两点,平行于直线l的直线m从原点O出发,沿x轴的正方向以每秒1个单位长度的速度运动,它与x轴、y轴分别交于M,N两点,设运动时间为t秒(0< t <4). (1)求A,B两点的坐标; (2)用含t的代数式表示△MON的面积S1; (3)以MN为对角线作矩形OMPN,记△MPN和△OAB重叠部分的面积为S2,试探究S2与t之间的函数关系式. 5、如图12, 四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4).点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动.其中一个动点到达终点时,另一个 动点也随之停止运动.过点N作NP垂直x轴于点P,连结AC交NP于Q,连结MQ. (1)点 (填M或N)能到达终点; (2)求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大; (3)是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标,若不存在,说明理由. 6、如图,在平面直角坐标系中,点A,B的坐标分别为A(4,0),B(0,-4),P为y轴上B点下方一点,PB=m(m>0),以点P为直角顶点,AP为腰在第四象限内作等腰Rt△APM. (1)求直线AB的解析式; (2)用含m的代数式表示点M的坐标; (3)若直线MB与x轴交于点Q,求点Q的坐标. 7、已知,如图,一次函数y=kx+b与x轴、y轴分别交于点A和点B,A点坐标为(3,0),∠OAB=45°. (1)求一次函数的表达式; (2)点P是x轴正半轴上一点,以P为直角顶点,BP为腰在第一象限内作等腰Rt△BPC,连接CA并延长交y轴于点Q. ①若点P的坐标为(4,0),求点C的坐标,并求出直线AC的函数表达式; ②当P点在x轴正半轴运动时,Q点的位置是否发生变化?若不变,请求出它的坐标;如果变化,请求出它的变化范围. 8、如图,以O为原点的直角坐标系中,A点的坐标为(0,1),直线x=1交x轴于点B.点为线段AB上一动点,作直线PC⊥PO,交直线x=1于点C.过P点作直线MN平行于x轴,交y轴于点M,交直线x=1于点N.记AP=x,△PBC的面积为S. (1)当点C在第一象限时,求证:△OPM≌△PCN; (2)当点P在线段AB上移动时,点C也随之在直线x=1上移动,求出S与x之间的函数关系式,并写出自变量的取值范围; (3)当点P在线段AB上移动时,△PBC是否可能成为等腰三角形?如果可能,直接写出所有能使△PBC成为等腰三角形的x的值;如果不可能,请说明理由. 9、如图,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知A点坐标为(a,0),B点坐标为(0,b),且a,b满足+|2a﹣b﹣2|=0.D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒1个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒. (1)当点P经过点C时,求直线DP的函数解析式; (2) ①求△OPD的面积S关于t的函数解析式; ②如图②,把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标. (3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由. 10.如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG. (1)求证:△AOG≌△ADG; (2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由; (3)当∠1=∠2时,求直线PE的解析式. 11.如图,点A在y轴上,点B在x轴上,且OA=OB=1,经过原点O的直线l交线段AB于点C,过C作OC的垂线,与直线x=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究: (1)当△AOC和△BCP全等时,求出t的值; (2)通过动手测量线段OC和CP的长来判断它们之间的大小关系并证明你得到的结论; (3)①设点P的坐标为(1,b),试写出b关于t的函数关系式和变量t的取值范围. ②求出当△PBC为等腰三角形时点P的坐标. 12.如图1,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC交于点C. (1)若直线AB解析式为y=﹣2x+12,直线OC解析式为y=x, ①求点C的坐标; ②求△OAC的面积. (2)如图2,作∠AOC的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为6,且OA=4,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由. 13.如图,在平面直角坐标系xOy中,已知直线PA是一次函数y=x+m(m>0)的图象,直线PB是一次函数y=﹣3x+n(n>m)的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点. (1)用m、n分别表示点A、B、P的坐标及∠PAB的度数; (2)若四边形PQOB的面积是,且CQ:AO=1:2,试求点P的坐标,并求出直线PA与PB的函数表达式; (3)在(2)的条件下,是否存在一点D,使以A、B、P、D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.14.如图,一次函数的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°. (1)求△ABC的面积; (2)如果在第二象限内有一点P(m,),试用含m的代数式表示△APB的面积,并求当△APB与△ABC面积相等时m的值; (3)是否存在使△QAB是等腰三角形并且在坐标轴上的点Q?若存在,请写出点Q所有可能的坐标;若不存在,请说明理由. 15、如图1,在平面直角坐标系中,直线AB与x轴交于点A,与y轴交于点B,与直线OC交于点C. (1)若直线AB解析式为y=﹣2x+12,直线OC解析式为y=x, ①求点C的坐标; ②求△OAC的面积. (2)如图2,作∠AOC的平分线ON,若AB⊥ON,垂足为E,△OAC的面积为6,且OA=4,P、Q分别为线段OA、OE上的动点,连接AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由. 16、如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根. (1)求C点坐标; (2)求直线MN的解析式; (3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标. 17、如图,在平面直角坐标系中,直线y= 分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),四边形ABCD是正方形.
(1)填空:b=________; (2)点D的坐标为________; (3)点M是线段AB上的一个动点(点A、B除外),在x轴上方是否存在另一个点N,使得以O、B、M、N为顶点的四边形是菱形?若不存在,请说明理由;若存在,请求出点N的坐标. 18、如图1,正方形ABCD的边长为4厘米,E为AD边的中点,F为AB边上一点,动点P从点B出发,沿B→C→D→E,向终点E以每秒a厘米的速度运动,设运动时间为t秒,△PBF的面积记为S. S与t的部分函数图象如图2所示,已知点M(1, )、N(5,6)在S与t的函数图象上.(1)求线段BF的长及a的值; (2)写出S与t的函数关系式,并补全该函数图象; (3)当t为多少时,△PBF的面积S为4.
T同步——同步训练
同步知识梳理
同步题型分析
A
B
C
O
x
y
C专题
T能力
图12
1
