人教版数学九年级上册第二十二章 二次函数复习讲义(无答案)
文档属性
| 名称 | 人教版数学九年级上册第二十二章 二次函数复习讲义(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 817.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-29 00:00:00 | ||
图片预览



文档简介
教师辅导讲义
学员编号: 年 级: 课 时 数: 学员姓名: 辅导科目: 学科教师:
授课类型 T同步(二次函数)
授课日期及时段
教学内容
(大脑放电影~) 知识点1:二次函数概念 二次函数的概念:一般地,形如(是常数,)的函数,叫做二次函数。 这里需要强调:和一元二次方程类似,二次项系数,而可以为零.二次函数的定义域是全体实数. 2. 二次函数的结构特征: (1)等号左边是函数,右边是关于自变量的二次式,的最高次数是2. (2)是常数,是二次项系数,是一次项系数,是常数项. 知识点2:二次函数解析式的表示方法 (1)一般式:y=ax2+bx+c (其中a,b,c是常数,a≠0); (2)顶点式:y=a(x-h)2+k (a≠0), 它直接显示二次函数的顶点坐标是(h,k); (3)交点式:y=a(x-x1)(x-x2)(a≠0), 其中x1,x2是图象与x轴交点的横坐标. 注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与轴有交点,即时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化,转化时a不变。 根据已知条件确定二次函数解析式,通常利用待定系数法.用待定系数法求二次函数的解析式必须根据题目的特点,选择适当的形式,才能使解题简便.一般来说,有如下几种情况: 1.一般式法 若已知条件是图象上三个点的坐标,则设一般式y=ax2+bx+c(a≠0),将已知条件代入,求出a,b,c的值. 2.顶点式法 若已知二次函数的顶点坐标或对称轴方程与最大值或最小值,则设顶点式y=a(x-h)2+k(a≠0),将已知条件代入,求出待定系数的值,最后将解析式化为一般式. 3.交点式法 若已知二次函数图象与x轴的两个交点的坐标,则设交点式y=a(x-x1)(x-x2)(a≠0),将第三点的坐标或其他已知条件代入,求出待定系数a的值,最后将解析式化为一般式. 知识点3:二次函数的图象与各项系数之间的关系 1. 二次项系数 二次函数中,作为二次项系数,显然. ⑴ 当时,抛物线开口向上,的值越大,开口越小,反之的值越小,开口越大; ⑵ 当时,抛物线开口向下,的值越小,开口越小,反之的值越大,开口越大. 总的说来,决定了抛物线开口的大小和方向,的正负决定开口方向,的大小决定开口的大小。 2. 一次项系数 在二次项系数确定的前提下,决定了抛物线的对称轴. 的符号的判定:对称轴在轴左边则,在轴的右侧则,即“左同右异” 3. 常数项 ⑴ 当时,抛物线与轴的交点在轴上方,即抛物线与轴交点的纵坐标为正; ⑵ 当时,抛物线与轴的交点为坐标原点,即抛物线与轴交点的纵坐标为; ⑶ 当时,抛物线与轴的交点在轴下方,即抛物线与轴交点的纵坐标为负. 总结起来,决定了抛物线与轴交点的位置. 总之,只要都确定,那么这条抛物线就是确定的、唯一的。 项目 字母 字母的符号图象的特征aa>0开口向上a<0开口向下bb=0对称轴为y轴ab>0(a与b同号)对称轴在y轴左侧ab<0(a与b异号)对称轴在y轴右侧cc=0经过原点c>0与y轴正半轴相交c<0与y轴负半轴相交
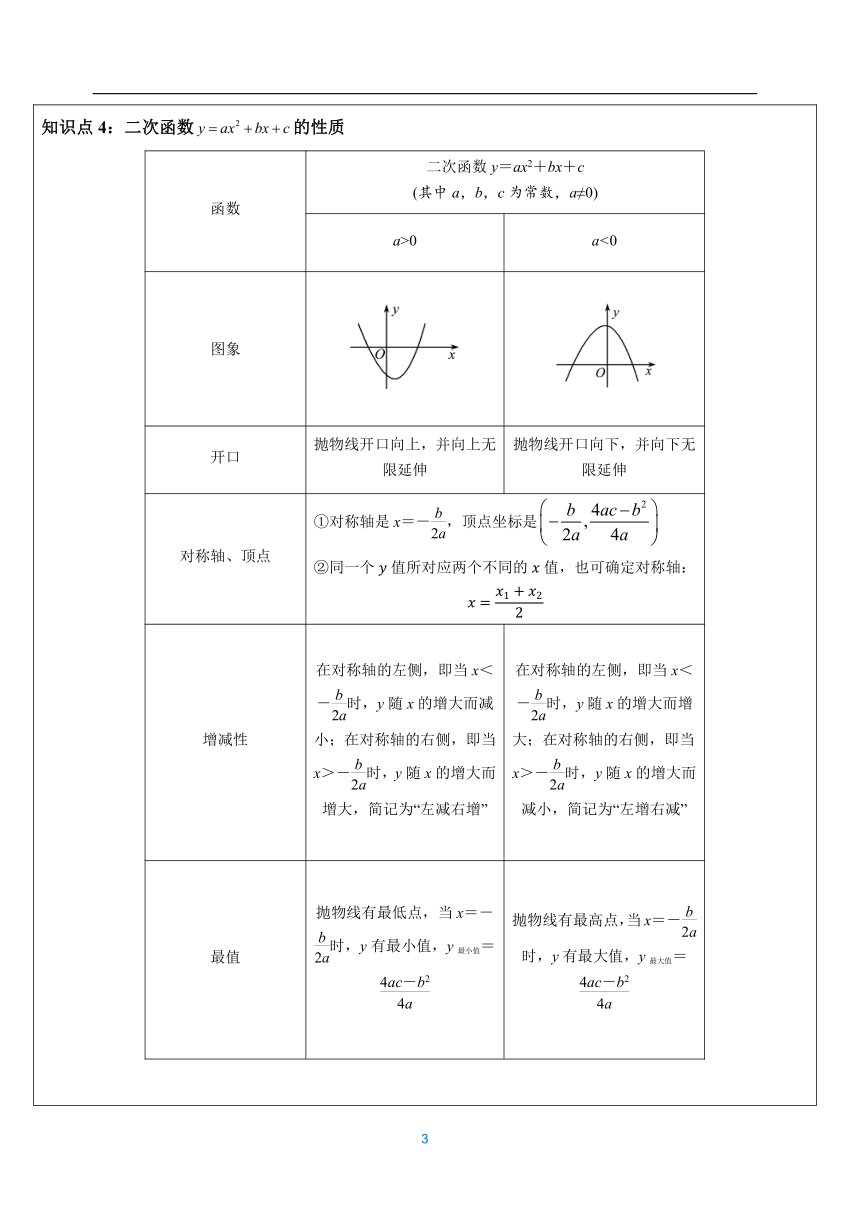
知识点4:二次函数的性质 函数二次函数y=ax2+bx+c (其中a,b,c为常数,a≠0)a>0a<0图象开口抛物线开口向上,并向上无限延伸抛物线开口向下,并向下无限延伸对称轴、顶点①对称轴是x=-,顶点坐标是 ②同一个值所对应两个不同的值,也可确定对称轴: 增减性在对称轴的左侧,即当x<-时,y随x的增大而减小;在对称轴的右侧,即当x>-时,y随x的增大而增大,简记为“左减右增”在对称轴的左侧,即当x<-时,y随x的增大而增大;在对称轴的右侧,即当x>-时,y随x的增大而减小,简记为“左增右减”最值抛物线有最低点,当x=-时,y有最小值,y最小值=抛物线有最高点,当x=-时,y有最大值,y最大值=
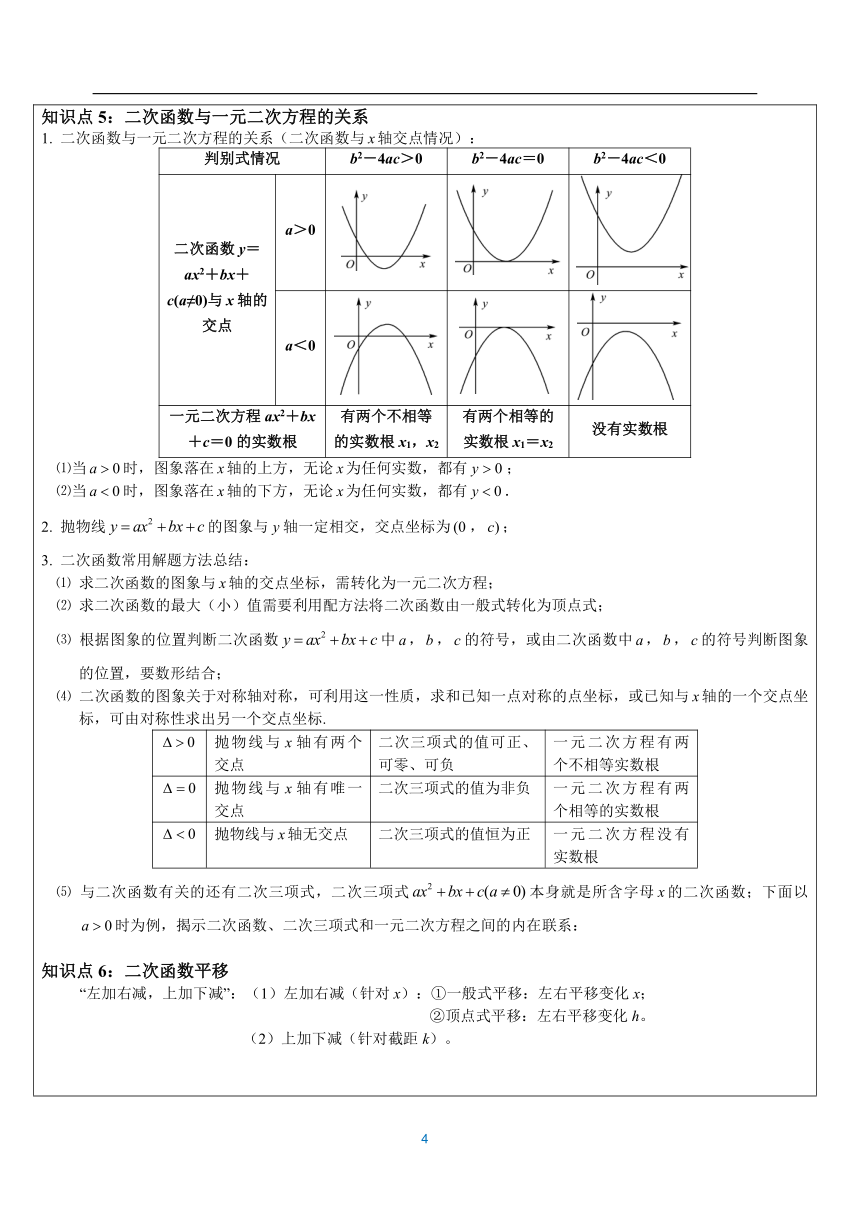
知识点5:二次函数与一元二次方程的关系 1. 二次函数与一元二次方程的关系(二次函数与轴交点情况): 判别式情况b2-4ac>0b2-4ac=0b2-4ac<0二次函数y=ax2+bx+c(a≠0)与x轴的交点a>0a<0一元二次方程ax2+bx+c=0的实数根有两个不相等的实数根x1,x2有两个相等的实数根x1=x2没有实数根
⑴当时,图象落在轴的上方,无论为任何实数,都有; ⑵当时,图象落在轴的下方,无论为任何实数,都有. 2. 抛物线的图象与轴一定相交,交点坐标为,; 3. 二次函数常用解题方法总结: ⑴ 求二次函数的图象与轴的交点坐标,需转化为一元二次方程; ⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式; ⑶ 根据图象的位置判断二次函数中,,的符号,或由二次函数中,,的符号判断图象的位置,要数形结合; ⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与轴的一个交点坐标,可由对称性求出另一个交点坐标. 抛物线与轴有两个交点二次三项式的值可正、可零、可负一元二次方程有两个不相等实数根抛物线与轴有唯一交点二次三项式的值为非负一元二次方程有两个相等的实数根抛物线与轴无交点二次三项式的值恒为正一元二次方程没有实数根
⑸ 与二次函数有关的还有二次三项式,二次三项式本身就是所含字母的二次函数;下面以时为例,揭示二次函数、二次三项式和一元二次方程之间的内在联系: 知识点6:二次函数平移 “左加右减,上加下减”:(1)左加右减(针对x):①一般式平移:左右平移变化x; ..②顶点式平移:左右平移变化h。 .(2)上加下减(针对截距k)。 任意抛物线y=a(x-h)2+k可以由抛物线y=ax2经过平移得到,具体平移方法如下: 1. 沿轴平移:向上(下)平移个单位,变成: (或) 2. 沿x轴平移:向左(右)平移个单位,变成: (或) 知识点7:二次函数图象的对称 二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达 1. 关于轴对称 关于轴对称后,得到的解析式是; 关于轴对称后,得到的解析式是; 2. 关于轴对称 关于轴对称后,得到的解析式是; 关于轴对称后,得到的解析式是; 3. 关于原点对称 关于原点对称后,得到的解析式是; 关于原点对称后,得到的解析式是; 4. 关于顶点对称(即:抛物线绕顶点旋转180°) 关于顶点对称后,得到的解析式是; 关于顶点对称后,得到的解析式是. 根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此永远不变.求抛物线的对称抛物线的表达式时,可以依据题意或方便运算的原则,选择合适的形式,习惯上是先确定原抛物线(或表达式已知的抛物线)顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后写出其对称抛物线的表达式. (热个身先~) 题型一:对称性 1、已知点A(a﹣2b,2﹣4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( ) A.(﹣3,7) B. (﹣1,7) C.(﹣4,10) D.(0,10) 2、当或()时,代数式的值相等,则时,代数式的值为 。 3、已知和时,多项式的值相等,且,则当时,多项式的值等于________。 4、已知二次函数图象上三点A(-1,y1),B(2,y2),C(4,y3),则y1、y2、y3的大小关系为( ) A.?y1
①抛物线与x轴的一个交点为(3,0);②函数的最大值为6;
③抛物线的对称轴是直线;?? ??? ④在对称轴左侧,y随x增大而增大. 6、(2019?长丰县二模)如图,菱形ABCD的三个顶点在二次函数y=ax2+2ax+2(a<0)的图象上,点A,B分别是该抛物线的顶点和抛物线与y轴的交点,则点D的坐标为 . 7、向空中发射一枚炮弹,经x秒后的高度为y米,且时间与高度的关系为y=ax2bxc(a≠0).若此炮弹在第7秒与第14秒时的高度相等,则在下列时间中炮弹所在高度最高的是( ) A.第8秒 B.第10秒 C.第12秒 D.第15秒 8、竖直上抛的小球离地高度是它运动时间的二次函数,小军相隔1秒依次竖直向上抛出两个小球,假设两个小球离手时离地高度相同,在各自抛出后1.1秒时到达相同的最大离地高度,第一个小球抛出后t秒时在空中与第二个小球的离地高度相同,则t=_____________ 9、(2018秋?大连期末)已知某种礼炮的升空高度h(m)与飞行时间t(s)的关系是h=﹣+20t+1,若此礼炮在升空到最高处时引爆,到引爆需要的时间为( ) A.6s B.5s C.4s D.3s 题型二:增减性 1、已知二次函数,当时,随着的增大而减小,则的取值范围是(?? ?) A. B. C. D. 2、若二次函数,当时,y随x的增大而减小,则m的取值范围是( ) A. B. C. D. 3、已知二次函数,当时,随的增大而增大,而的取值范围是( ) A. B. C. D. 4、(2019?滨江区一模)已知二次函数y=ax2+(a+2)x﹣1(a为常数,且a≠0),( ) A.若a>0,则x<﹣1,y随x的增大而增大 B.若a>0,则x<﹣1,y随x的增大而减小 C.若a<0,则x<﹣1,y随x的增大而增大 D.若a<0,则x<﹣1,y随x的增大而减小 题型三:最值 1、已知二次函数,当x取任意实数时,都有y>0,则m的取值范围是( ) A. B. C. D. 若变量y与变量x的函数关系是,在范围内的最大值为2,则常数m的值为___________ 3、(2019?南昌二模)如图,P是抛物线y=x2﹣x﹣4在第四象限的一点,过点P分别向x轴和y轴作垂线,垂足分别为A、B,则四边形OAPB周长的最大值为( ) A.10 B.8 C.7.5 D.5 4、(2019?温州)已知二次函数y=x2﹣4x+2,关于该函数在﹣1≤x≤3的取值范围内,下列说法正确的是( ) A.有最大值﹣1,有最小值﹣2 B.有最大值0,有最小值﹣1 C.有最大值7,有最小值﹣1 D.有最大值7,有最小值﹣2 题型四:图像题 1、在平面直角坐标系xOy中,四条抛物线如图所示,其表达式中的二次项系数绝对值最小的是( ) A.y1 B.y2 C.y3 D.y4 2、如图,二次函数的图象开口向下,且经过第三象限的点P.若点P的横坐标为-1,则一次函数的图象大致是( ) A. B. C. D. 3、在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是( ) A. B. C. D. 4、在同一直角坐标系中,函数和(是常数,且)的图象可能是( ) A. B.C. D. 5、二次函数的图象如图所示,则一次函数与反比例函数在同一坐标系内的图象大致为( ) A. B. C. D. 6、(西固区校级模拟)图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是( ) A.y=﹣2x2 B.y=2x2 C.y=﹣0.5x2 D.y=0.5x2 7、(硚口区期中)如图是抛物线形拱桥,当拱顶高离水面2m时,水面宽4m,水面下降2.5m,水面宽度增加( ) A.1 m B.2 m C.3 m D.6 m 题型五:图象与系数问题 1、二次函数的图象如图所示,对称轴是直线,下列结论: ①;②;③;④. 其中正确的是( ) A.①④ B.②④ C. ①②③ D.①②③④ 2、(2019?鄞州区一模)y=ax2+bx+c的图象如图所示,则下列4个代数式a+2b+c,2a+b+c,3a+2b+c,﹣,其中值一定大于1的个数是( ) A.1个 B.2个 C.3个 D.4个 3、(2019?麻城市校级自主招生)如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中﹣1<x1<0,1<x2<2,下列结论:4a+2b+c<0,2a+b<0,b2+8a>4ac,a<﹣1,其中结论正确的有( ) A.1个 B.2个 C.3个 D.4个 4、如图是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点是B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论: ①abc>0;②方程ax2+bx+c=3有两个相等的实数根;③抛物线与x轴的另一个交点是(﹣1,0);④当1<x<4时,有y2>y1;⑤x(ax+b)≤a+b, 其中正确的结论是 .(只填写序号) 5、如图是二次函数y=ax2+bx+c的图象的一部分;图象过点A(-3,0),对称轴为x=-1,给出四个结论: ①b2>4ac;②2a+b=0;③a-b+c=0;④5a<b. 其中正确的是_____________.(填序号) 题型六:交点问题 1、若函数y=mx2+(m+2)x+m+1的图象与x轴只有一个交点,那么m的值为( ) A.0 B.0或2 C.2或-2 D.0,2或-2 2、若函数的图象与轴只有一个交点,则的值为________ 3、若二次函数的图象与轴只有一个交点,那么的值为__________ 4、二次函数与坐标轴有且只有两个交点,则的值为___________ 题型七:平移问题 1、把抛物线向右平移3个单位,再向下平移2个单位,所得图象的解析式是,则( ) A. , B. , C. , D. , 2、(2019?南市区一模)把二次函数y=(2x﹣1)2+3的图象,先向左平移1个单位,再向上平移1个单位,平移后的二次函数解析式为( ) A.y=2x2+4 B.y=4x2+4x+5 C.y=4x2﹣4x+5 D.y=4x2+4x+4 3、在同一平面直角坐标系内,将函数y=2x2+4x-3的图象向右平移2个单位,再向下平移1个单位,得到的图象的顶点坐标是( ) A.(-3,-6) B.(1,-4) C.(1,-6) D.(-3,-4) 4、(2019?玉环市一模)把抛物线y=ax2+bx+c图象先向左平移2个单位长度,再向下平移3个单位长度,所得的图象的解析式是y=x2+5x+6,则a﹣b+c的值为( ) A.2 B.3 C.5 D.12 题型八:对称变换 1、在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点选择180°得到抛物线y=x2+5x+6,则原抛物线的解析式是( ) y=-(x-)2- B.y=-(x+)2- C.y=-(x-)2- D.y=-(x+)2+ 2、(2015?湖州)如图,已知抛物线C1:y=a1x2+b1x+c1和C2:y=a2x2+b2x+c2都经过原点,顶点分别为A,B,与x轴的另一交点分别为M,N,如果点A与点B,点M与点N都关于原点O成中心对称,则称抛物线C1和C2为姐妹抛物线,请你写出一对姐妹抛物线C1和C2,使四边形ANBM恰好是矩形,你所写的一对抛物线解析式是 . 3、已知二次函数,求满足下列条件的二次函数的解析式: (1)图象关于轴对称; (2)图象关于y轴对称; (3)图象关于原点对称; (4)图象关于经过其顶点且平行于x轴的直线对称。 题型九:二次函数与一元二次方程、一元二次不等式(数形结合问题) 1.已知二次函数(为常数)的图象与轴的一个交点为,则关于的一元二次方程的两实数根是( ) A., B., C., D., 2.关于的方程(、、均为常数,)的解是,,则方程的解是( ) A., B., C., D., 3.二次函数的图象如图,若一元二次方程有实数根,则的最大值为( ) A.-3 B.3 C.-6 D.9 4.“如果二次函数的图象与轴有两个公共点,那么一元二次方程有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若、是关于的方程的两根,则、、、的大小关系是( ) A. B. C. D. 5.已知函数,若使成立的值恰好有三个,则的值为( ) A.0 B.1 C.2 D.3 6.二次函数的图象如图,对称轴为直线,若关于的一元二次方程(为实数)在的范围内有解,则的取值范围是( ) A. B. C. D. 题型十:二次函数的应用(函数模型与意义) 1、教练对小明推铅球的录像进行技术分析,发现铅球行进高度(单位:)与水平距离(单位:)之间的关系为,由此可知铅球推出的距离是________。 2、某种火箭被竖直向上发射时,它的高度(单位:)与时间(单位:)的关系可以用公式表示,经过________,火箭达到它的最高点,最高高度为________。 3、某高尔夫运动员打尔夫球,若球的飞行高度(单位:)与水平距离(单位:)之间的函数表达式为,则高尔夫球在飞行过程中的最大高度为________。 4、某一型号飞机着陆后滑行的距离(单位:)与滑行时间(单位:)之间的函数关系式是,该型号飞机着陆后滑行________才能停下来。 5、某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台. (1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围) (2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元? (3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少? 6、(2014?台州)某公司经营杨梅业务,以3万元/吨的价格向农户收购杨梅后,分拣成A、B两类,A类杨梅包装后直接销售;B类杨梅深加工后再销售.A类杨梅的包装成本为1万元/吨,根据市场调查,它的平均销售价格y(单位:万元/吨)与销售数量x(x≥2)之间的函数关系如图;B类杨梅深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨. (1)直接写出A类杨梅平均销售价格y与销售量x之间的函数关系式; (2)第一次,该公司收购了20吨杨梅,其中A类杨梅有x吨,经营这批杨梅所获得的毛利润为w万元(毛利润=销售总收入﹣经营总成本). ①求w关于x的函数关系式; ②若该公司获得了30万元毛利润,问:用于直销的A类杨梅有多少吨? (3)第二次,该公司准备投入132万元资金,请设计一种经营方案,使公司获得最大毛利润,并求出最大毛利润.
1
同课章节目录
