人教版八年级上册 11.3多边形及其内角和辅导讲义(无解析)
文档属性
| 名称 | 人教版八年级上册 11.3多边形及其内角和辅导讲义(无解析) |  | |
| 格式 | zip | ||
| 文件大小 | 441.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-29 23:53:09 | ||
图片预览




文档简介
教师辅导讲义
学员编号: 年 级: 课 时 数: 学员姓名: 辅导科目: 学科教师:
授课类型 T多边形及其内角和
授课日期及时段
教学内容
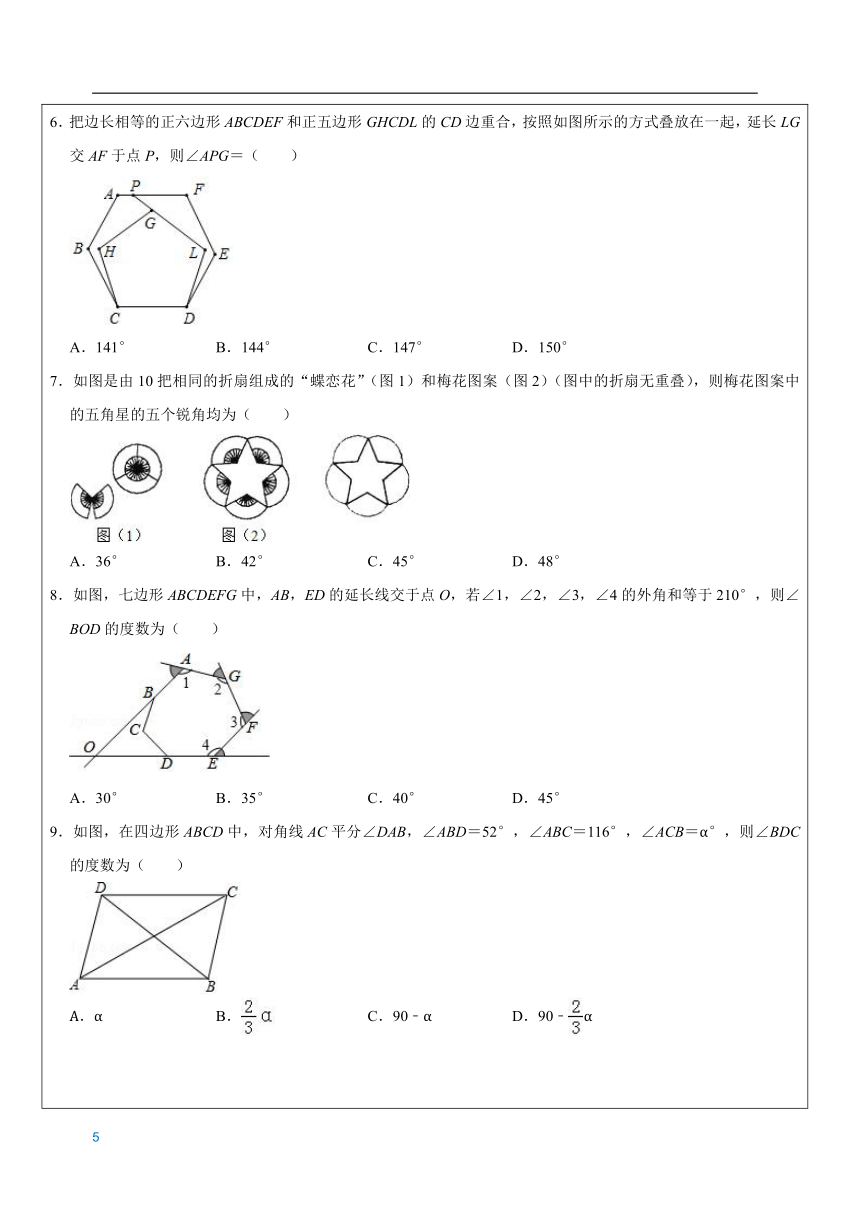
同步知识梳理 知识点:多边形及其内角和 (1)在平面内,由一些线段首位顺次相接组成的图形叫做多边形. 如果一个多边形由n条线段组成,那么这个多边形叫做n边形。(一个多边形由几条线段组成,就叫做几边形。) (2)多边形的边、顶点、内角和外角、对角线 多边形的内角:多边形相邻两边组成的角 多边形的外角:多边形的边与它的邻边的延长线组成的角 多边形的对角线:连接多边形的不相邻的两个顶点的线段(对角线公式:) 注:一个n边形,过一个顶点可以作(n-3)条对角线,可以分成(n-2)个三角形. (3)凸多边形与凹多边形 在图(1)中,画出四边形ABCD的任何一条边所在的直线,整个图形都在这条直线的同一侧,这样的四边形叫做凸四边形,这样的多边形称为凸多边形; 而图(2)就不满足上述凸多边形的特征,因为我们画BD所在直线,整个多边形不都在这条直线的同一侧,我们称它为凹多边形,今后我们在习题、练习中提到的多边形都是凸多边形. (4)正多边形:由正方形的特征出发,得出正多边形的概念. 各个角都相等,各条边都相等的多边形叫做正多边形. (5)多边形的内角和、外角和 多边形内角和定理:n边形的内角的和等于: (n - 2)×180°(n大于等于3且n为整数)。 多边形的外角和:多边形的外角和等于360°。 二、同步题型分析 题型1:多边形 1.将一个四边形截去一个角后,它不可能是( ) A.六边形 B.五边形 C.四边形 D.三角形 2.从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成( )个三角形. A.6 B.5 C.8 D.7 3.一个多边形截去一角后,变成一个八边形则这个多边形原来的边数是( ) A.8或9 B.7或8 C.7或8或9 D.8或9或10 4.从n边形的一个顶点出发作对角线,这些对角线把这个n边形分成的三角形个数为( ) A.(n+1)个 B.n个 C.(n﹣1)个 D.(n﹣2)个 5.从多边形一个顶点出发向其余的顶点引对角线,将多边形分成6个三角形,则此多边形的边数为( ) A.6 B.7 C.8 D.9 6.我们知道,四边形有2条对角线,五边形有5条对角线,那么十二边形的对角线总条数是( ) A.9 B.54 C.60 D.108 7.如图是由相同的花盆按一定的规律组成的正多边形图案,其中第1个图形一共有6个花盆,第2个图形一共有12个花盆,第3个图形一共有20个花盆,…,则第n个图形中花盆的个数为 . 8.我们把正n边形(n≥3)的各边三等分,分别以居中的那条线段为一边向外作正n边形,并去掉居中的那条线段,得到一个新的图形叫做正n边形的“扩展图形”,并将它的边数记为an.如图1,将正三角形进行上述操作后得到其“扩展图形”,且a3=12.图3、图4分别是正五边形、正六边形的“扩展图形”. (1)如图2,在5×5的正方形网格中用较粗的虚线画有一个正方形,请在图2中用实线画出此正方形的“扩展图形”; (2)已知a3=12,a4=20,a5=30,则图4中a6= ,根据以上规律,正n边形的“扩展图形”中an= ;(用含n的式子表示) (3)已知=﹣,=﹣,=﹣,…,且+++…+=,则n= . 题型2:多边形及其内角和 1.如图,足球图片正中的黑色正五边形的内角和是( ) A.180° B.360° C.540° D.720° 2.如果一个多边形的内角和等于1440°,那么这个多边形的边数为( ) A.8 B.9 C.10 D.11 3.小明在计算一个多边形的内角和时,漏掉了一个内角,结果算得800°,这个多边形应该是( ) A.六边形 B.七边形 C.八边形 D.九边形 4.如图,M是正六边形ABCDEF的边CD延长线上的一点,则∠ADM的度数是( ) A.135° B.120° C.108° D.60° 5.将若干个大小相等的正五边形排成环状,如图所示是前3个五边形,要完成这一圆环还需_______个正五边形( ) A.6 B.7 C.8 D.9 6.把边长相等的正六边形ABCDEF和正五边形GHCDL的CD边重合,按照如图所示的方式叠放在一起,延长LG交AF于点P,则∠APG=( ) A.141° B.144° C.147° D.150° 7.如图是由10把相同的折扇组成的“蝶恋花”(图1)和梅花图案(图2)(图中的折扇无重叠),则梅花图案中的五角星的五个锐角均为( ) A.36° B.42° C.45° D.48° 8.如图,七边形ABCDEFG中,AB,ED的延长线交于点O,若∠1,∠2,∠3,∠4的外角和等于210°,则∠BOD的度数为( ) A.30° B.35° C.40° D.45° 9.如图,在四边形ABCD中,对角线AC平分∠DAB,∠ABD=52°,∠ABC=116°,∠ACB=α°,则∠BDC的度数为( ) α B. C.90﹣α D.90﹣α 10.如图,小明从点A出发,前进5m后向右转20°,再前进5m后又向右转20°,这样一直下直到他第一次回到出发点A为止,他所走的路径构成了一个多边形. (1)小明一共走了 米; (2)这个多边形的内角和是 度. 11.如图,两直线AB与CD平行,则∠1+∠2+∠3+∠4+∠5+∠6= °. 证明题: 1.如图,证明:∠1+∠2=∠C+∠D 2.如图,求证:∠A+∠B+∠C+∠D +∠E=180° 3.已知:如图,∠CBE、∠BCF的平分线BP、CP交于点P 求证:∠P=90°-∠A 4.已知:如图,∠ABC、∠ACD的平分线BP、CP交于点P 求证:∠P=∠A 三、课堂达标检测 一、选择题 1.正多边形的一个内角为135°,则该多边形的边数为( ) A.5B.6C.7D.8
2.如图所示,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,且△ABC的面积是4cm2,则阴影部分面积等于( ) A.2cm2B.1cm2C.0.25cm2D.0.5cm2
3.已知三角形的两边长分别为5cm和9cm,则下列长度的四条线段中,不能作为第三边的是( ) A. 4cm B.6cm C.8cm D.13cm 4.如果三角形的一个外角小于与它相邻的内角,那么这个三角形一定是( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.任意三角形 5.如图,在△ABC中,∠BAC=90°,AC≠AB,AD是斜边BC上的高,DE⊥AC,DF⊥AB,垂足分别为E、F,则图中与∠C(∠C除外)相等的角的个数是( ) A.3个 B.4个 C.5个 D.6个 6.如图,将一副三角板叠放在一起,使直角的顶点重合于点O,AB∥OC,与OA交于点E,已知∠A=30°,∠C=45°,则∠DEO的度数为( ) A.45° B.60° C.70° D.75° 二、填空题 1.如图,将一副三角板叠放在一起,使直角顶点重合于O,则∠AOC+∠DOB= 2.如图,DE⊥AB,∠A=25°,∠D=35°,则∠ACB的度数为________________. 3.如图,为了使木门不变形,木工师傅在木门上加钉了一根木条,这样是利用三角形的________________. 4.把一副常用的三角板如图所示拼在一起,使B、C、E在同一直线上.那么图中∠ACD是________________. 5. 如图,七星形中∠A+∠B+∠C+∠D+∠E+∠F+∠G= 6.如图,⊿ABC中,∠A = 40°,∠B = 72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE, 则∠CDF = 度。 7.如果将长度为a-2、a+5和a+2的三根线段首尾顺次相接可以得到一个三角形,那么a的取值范围是 8. 如图所示,∠1=60°,则∠A+∠B+∠C+∠D+∠E+∠F的度数为 __________ 三、解答题 1.已知:如图1,在△ABC中,CD是高,若∠A=∠DCB.
(1)试说明∠ACB=90°;
(2)如图2,若AE是角平分线,AE、CD相交于点F.求证:∠CFE=∠CEF. 2. 如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E, ∠A=35°,∠D=42°,求∠ACD的度数. 3.已知:点D是△ABC所在平面内一点,连接AD、CD.
(1)如图1,若∠A=28°,∠B=72°,∠C=11°,求∠ADC;
(2)如图2,若存在一点P,使得PB平分∠ABC,同时PD平分∠ADC,探究∠A,∠P,∠C的关系并证明;
(3)如图3,在?(2)的条件下,将点D移至∠ABC的外部,其它条件不变,探究∠A,∠P,∠C的关系并证明.
4.三角形不等式是指一个三角形的两边长度之和大于第三边的长度.在下图中,E位于线段CA上,D位于线段BE上. (1)证明:AB+AE>DB+DE; (2)证明:AB+AC>DB+DC; (3)AB+BC+CA与2(DA+DB+DC)哪一个更大?证明你的结论; (4)AB+BC+CA与DA+DB+DC哪一个更大?证明你的结论. 5. 如图,∠MON=90°,点A、B分别在射线PM、PN上,∠MAB和∠NBA的平分线相交于点P.点A和点B在运动过程中,∠P的大小是否发生变化?请说明你的理由. 6. 如图,已知AB∥CD,BD平分∠ABC交AC于点O,CE平分∠DCG.若∠ACE=90°,试判断BD与AC的位置关系,并说明理由. 7. 如图①,则∠1+∠2+∠3+∠4 = °; 如图②,则∠1+∠2+∠3+∠4 +∠5 = °; 如图③,则∠1+∠2+∠3+∠4 +∠5+∠6 = °. 8. 已知:如图,在△ABC中,BO1、BO2是∠ABC的三等分线,CO1、CO2是∠ACB的三等分线. (1)当∠A=60°时,∠BO2C= °; (2)探索∠BO1C与∠BO2C之间的数量关系,并证明你的结论. 9. 如图,线段AB、CD交于点O,连接AD、BC,我们把形如图1的图形称为“8字形”. (1)如图(1),直接写出∠A+∠D与∠B+∠C的关系; (2)如图(2),∠DAB和∠BCD的平分线AP、CP交于点P,且分别与AB、CD交于点M、N,∠D=46°,∠B=30°. 先观察图中还有哪些“8字形”,再利用(1)的结论求∠P的度数; (3)在(2)中,若∠D=α,∠B=β,直接写出∠P的度数(用含有α、β的式子表示). 10.如图,△ABC中,∠ABC的角平分线与∠ACB的外角∠ACD的平分线交于A1.
(1)当∠A为70°时,
∵∠ACD-∠ABD=∠____ ∴∠ACD-∠ABD=______°
∵BA1、CA1是∠ABC的角平分线与∠ACB的外角∠ACD的平分线
∴∠A1CD-∠A1BD=(∠ACD-∠ABD)
∴∠A1=______°;
(2)∠A1BC的角平分线与∠A1CD的角平分线交于A2,∠A2BC与A2CD的平分线交于A3,如此继续下去可得A4、…、An,请写出∠A与∠An的数量关系___________;
(3)如图2,四边形ABCD中,∠F为∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的角,若∠A+∠D=230度,则∠F=____________.
(4)如图3,若E为BA延长线上一动点,连EC,∠AEC与∠ACE的角平分线交于Q,当E滑动时有下面两个结论:①∠Q+∠A1的值为定值;②∠Q-∠A1的值为定值.其中有且只有一个是正确的,请写出正确的结论,并求出其值. 11. 如图,四边形ABCD中,内角∠ABC的角平分线与外角∠DCE的角平分线交于点F,且∠F为锐角.设∠A=α,∠D=β. 如图①,α+β>180°,试用α、β表示∠F; 如图②,α+β<180°,请在图中画出∠F,并试用α、β表示∠F; 一定存在∠F吗?如有,求出∠F的值;如不一定,指出α、β满足什么条件时,不存在∠F. 12. 如图,长方形纸片ABCD,点E是AB上一动点,M是BC上一点,N是AD上一点,将△EAN沿EN翻折得到△EA′N,将△EBM沿EM翻折得到△EB′M.
(1)若∠A′EB′=80°,EN以2°/秒的速度顺时针旋转,若EM以4°/秒的速度逆时针旋转,t秒后,EA′与EB′重合,求t的值.
(2)若继续旋转,使EB′平分∠A′EN,探究∠A′EN与∠B′EM的数量关系.
13.如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于G,若∠BDC=140°,∠BGC=110°,求∠A的大小. 14.阅读下面材料:
小明遇到这样一个问题;
△ABC中,有两个内角相等.
①若∠A=110°,求∠B的度数;
②若∠A=40°,求∠B的度数.
小明通过探究发现,∠A的度数不同,∠B的度数的个数也可能不同,因此为同学们提供了如下解题的想法:
对于问题①,根据三角形内角和定理,∵∠A=110°>90°,∠B=∠C=35°;
对于问题②,根据三角形内角和定理,∵∠A=40°<90°,∴∠A=∠B或∠A=∠C或∠B∠C,∴∠B的度数可求.
请回答:
(1)问题②中∠B的度数为________;
(2)参考小明解决问题的思路,解决下面问题:
△ABC中,有两个内角相等.设∠A=x°,当∠B有三个不同的度数时,求∠B的度数(用含x的代式表示)以及x的取值范围.
17
