人教版八年级上册 12.2全等三角形的三种判定方法辅导讲义(无解析)
文档属性
| 名称 | 人教版八年级上册 12.2全等三角形的三种判定方法辅导讲义(无解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 268.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-29 00:00:00 | ||
图片预览



文档简介
教师辅导讲义
学员编号: 年 级: 课 时 数:学员姓名: 辅导科目: 学科教师:
授课类型 T同步( 全等三角形判定 )
授课日期及时段
教学内容
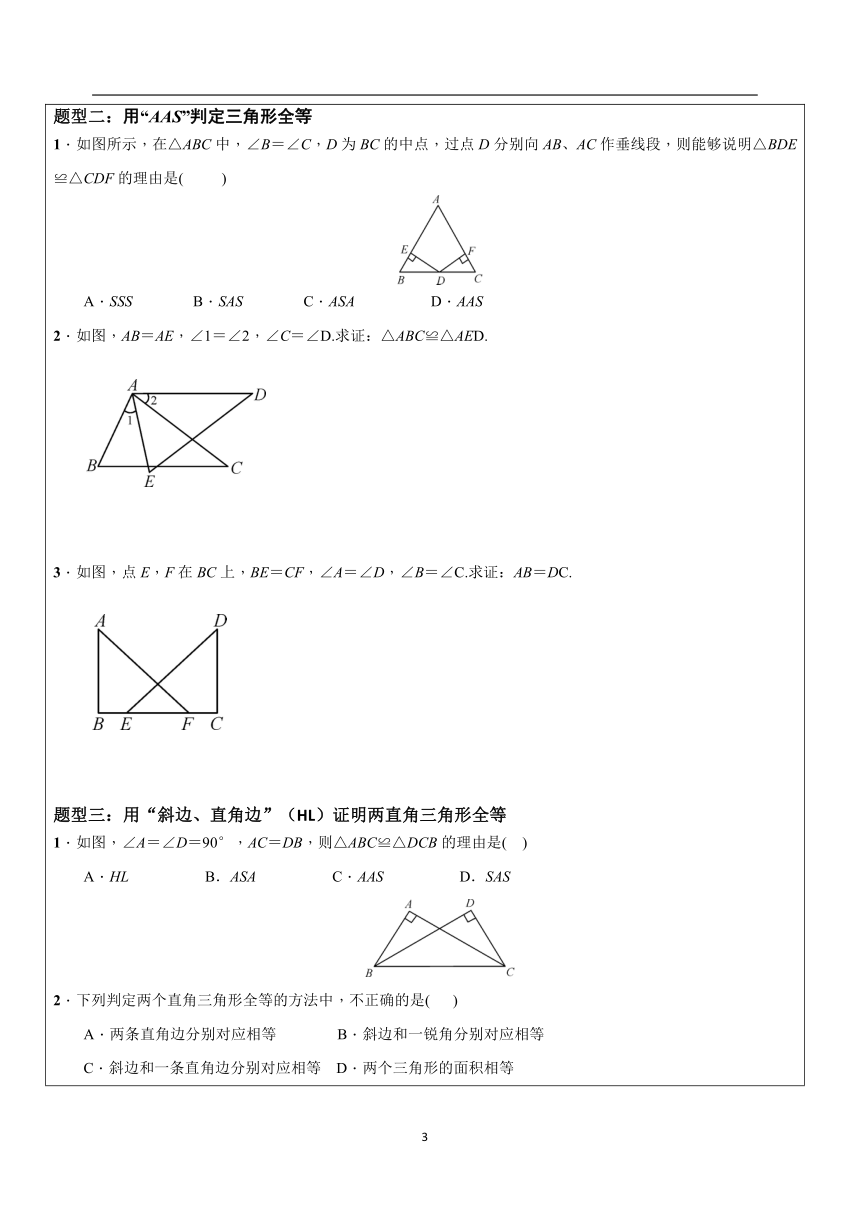
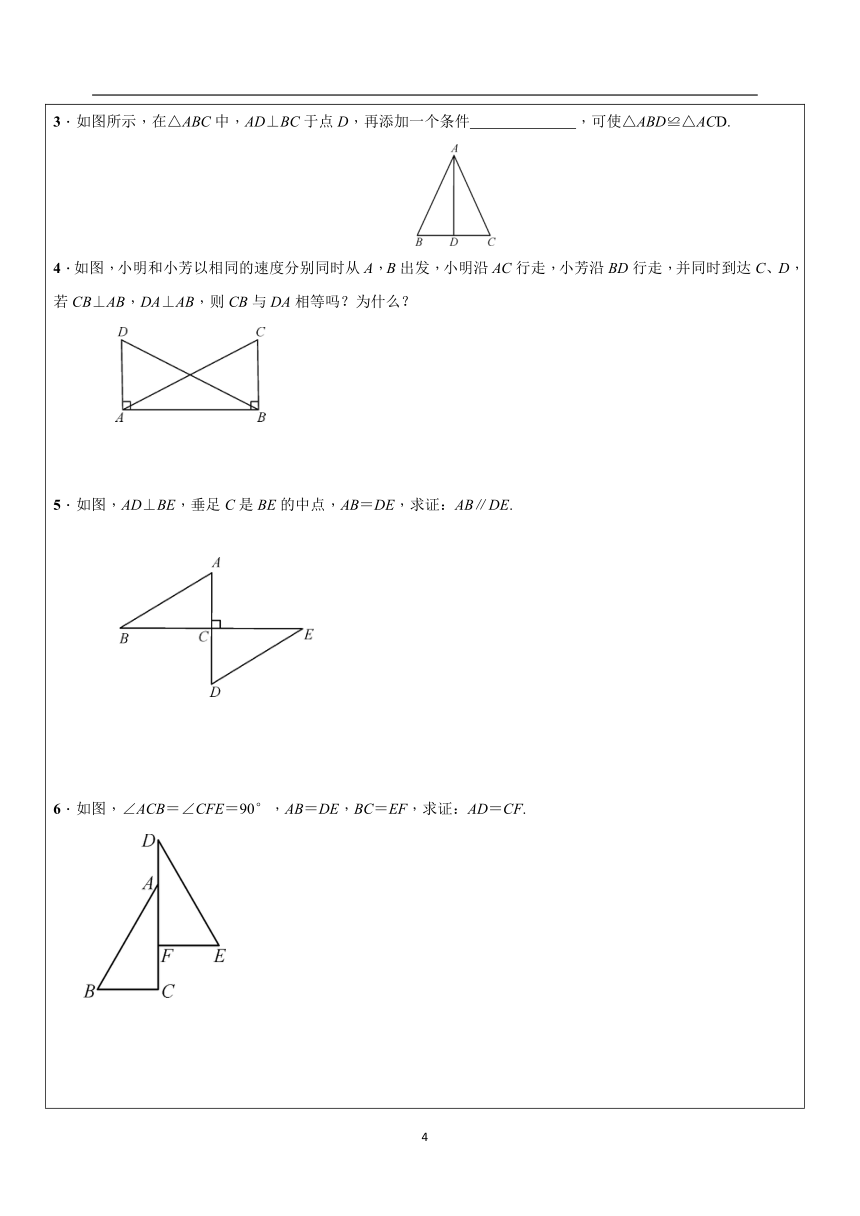
一、同步知识梳理知识点一:全等三角形判定方法三两角和它们的夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”)注意:书写格式在△ABC和△A′B′C′中 ∠A=∠A′ AB= A′B′ ∴△ABC≌△A′B′C′(ASA) ∠B=∠B′ 知识点二:全等三角形判定方法四两角和其中一角的对边分别相等的两个三角形全等(简写成“角角边”或“AAS”)注意:书写格式在△ABC和△A′B′C′中 ∠A=∠A′ ∠B=∠B′ ∴△ABC≌△A′B′C′(AAS) BC=B′C′ 知识点三:全等三角形判定方法五斜边和一条直角边分别相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”)注意:书写格式在Rt△ABC和Rt△A′B′C′中 AB=A′B′AC=A′C′(或BC=B′C′) ∴Rt△ABC≌Rt△A′B′C′(HL) (大脑放电影~)题型一:用角边角(ASA)证明两三角形全等1.如图,已知△ABC三条边、三个角,则甲、乙两个三角形中和△ABC全等的图形是( ) A.甲 B.乙 C.甲和乙都是 D.都不是2.如图,EC=AC,∠BCE=∠DCA,∠A=∠E,求证:BC=DC. 3.如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD. 题型二:用“AAS”判定三角形全等1.如图所示,在△ABC中,∠B=∠C,D为BC的中点,过点D分别向AB、AC作垂线段,则能够说明△BDE≌△CDF的理由是( )A.SSS B.SAS C.ASA D.AAS2.如图,AB=AE,∠1=∠2,∠C=∠D.求证:△ABC≌△AED. 3.如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C.求证:AB=DC. 题型三:用“斜边、直角边”(HL)证明两直角三角形全等1.如图,∠A=∠D=90°,AC=DB,则△ABC≌△DCB的理由是( )A.HL B.ASA C.AAS D.SAS2.下列判定两个直角三角形全等的方法中,不正确的是( )A.两条直角边分别对应相等 B.斜边和一锐角分别对应相等C.斜边和一条直角边分别对应相等 D.两个三角形的面积相等3.如图所示,在△ABC中,AD⊥BC于点D,再添加一个条件 ,可使△ABD≌△ACD. 4.如图,小明和小芳以相同的速度分别同时从A,B出发,小明沿AC行走,小芳沿BD行走,并同时到达C、D,若CB⊥AB,DA⊥AB,则CB与DA相等吗?为什么? 5.如图,AD⊥BE,垂足C是BE的中点,AB=DE,求证:AB∥DE. 6.如图,∠ACB=∠CFE=90°,AB=DE,BC=EF,求证:AD=CF. 题型四:三角形全等判定的选用1、杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下: 如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD,垂足为D,已知AB=20 m,请根据上述信息求标语CD的长度. 2、如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.(1)从图中任找两组全等三角形;(2)从(1)中任选一组进行证明. 3、如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE.求证:BC=BE. 4、如图1所示,在△ABC中, ∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥MN于点M,BN⊥MN于点N.(1)求证:MN=AM+BN;(2)如图2,若过点C作直线MN与线段AB相交,AM⊥MN于点M,BN⊥MN于点N(AM>BN),(1)中的结论是否仍然成立?说明理由. (你都掌握了没有呢~~~) 1. 如图,玻璃三角板摔成三块,现在到玻璃店在配一块同样大小的三角板,最省事的方法() A. 带①去 B. 带②去 C. 带③去 D.带①②③去2. 如图,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )AB=AC B. BD=CD C. ∠B=∠C D.∠BDA=∠CDA 3. 如图,给出下列四组条件: ①;②; ③;④. 其中,能使的条件共有() A.1组 B.2组 C.3组 D.4组 4.如图,,,,结论:①;②; ③; ④.其中正确的有()A.1个 B.2个 C.3个 D.4个 ?5.已知在△ABC和△DEF中,∠A=∠D=90°,则下列条件中不能判定△ABC和△DEF全等的是( ) A.AB=DE,AC=DF? B.AC=EF,BC=DF ? C.AB=DE,BC=EF? D.∠C=∠F,BC=EF ?6. 如图,AB∥EF∥DC,∠ABC=90°,AB=DC,那么图中有全等三角形( ) ?A.5对; B.4对; C.3对; D.2对 ?7. 要判定两个直角三角形全等,下列说法正确的有(? ) ? ①有两条直角边对应相等; ②有两个锐角对应相等; ③有斜边和一条直角边对应相等; ④有一条直角边和一个锐角相等; ⑤有斜边和一个锐角对应相等; ⑥有两条边相等. ? A.6个? B.5个? C.4个? D.3个 8. 如图,已知那么添加下列一个条件后,仍无法判定的是() A. B.;C. ;D.二、填空题9. 如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中和△ABC全等的图形是__________ 10.如图,△ABC中,BD=EC,∠ADB=∠AEC,∠B=∠C,则∠CAE=___________. 11. 如图,点B、E、F、C在同一直线上,已知∠A =∠D,∠B =∠C,要使△ABF≌△DCE,以“AAS”需要补充的一个条件是______________________(写出一个即可).12.如图,AD=BC,AC=BD,则图中全等三角形有_________对. 13.如图,已知∠1=∠2=90°,AD=AE,那么图中有 对全等三角形.14.如图,Rt△ABC中,∠C=90°,AC=8,BC=4,PQ=AB,点P与点Q分别在AC和AC的垂线AD上移动,则当AP=_______时,△ABC≌△APQ.15.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=4cm,CE=3cm,则DE=________cm . 16.如图,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=__________度 三、解答题17. 已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.求证:AB=DC 18.如图,已知AD是△ABC的角平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,需添加一个条件是:_______________,并给予证明. 19.如图,已知点在线段上,,请在下列四个等式中, ①AB=DE,②∠ACB=∠F,③∠A=∠D,④AC=DF.选出两个作为条件,推出.并予以证明.(写出一种即可) 已知: , . 求证:. 证明:
T同步——全等三角形的判定同步训练
同步知识梳理
课堂达标检测
第9题图
