人教版八年级上册12.3角平分线性质辅导讲义(无解析)
文档属性
| 名称 | 人教版八年级上册12.3角平分线性质辅导讲义(无解析) |  | |
| 格式 | zip | ||
| 文件大小 | 134.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 00:00:47 | ||
图片预览



文档简介
(大脑放电影~)
知识点1:角的平分线的概念:从角的顶点出发,等分这个角的射线,叫做这个角的平分线。
角是轴对称图形,它的对称轴是这个平分线所在的直线。
知识点2:角的平分线性质:在角的平分线上的点到这个角的两边的距离相等。
知识点3:角的平分线性质的逆定理:在一个角的内部(包括顶点)且到角的两边距离相等的点在这个角的平分线上。
角的平分线可以看作这个角的内部(包括顶点)到角的两边距离相等的点的集合。
(热个身先~~~)
题型一:角平分线性质
1、如图,OP平分∠AOB,PC⊥OA,垂足为C,PD⊥OB,垂足为D,则PC与PD的大小关系是( )
A.PC>PD B.PC=PD C.PC
【例2】如图所示,已知,△ABC中,∠C=,AD是∠BAC的平分线,DE⊥AB于点E,F在AC上,BE=CF,
求证:BD=DF
【巩固练习】
1.如图,下列推理中正确的个数是( )
①因为OC平分∠AOB,点P、D、E分别在OC、OA、OB上,所以PD=PE;
②因为P在OC上,PD⊥OA,PE⊥OB,所以PD=PE;
③因为P在OC上,PD⊥OA,PE⊥OB,且OC平分∠AOB,所以PD=PE
A、0个 B、1个 C、2个 D、3个
2.如图,P是∠AOB的平分线上的一点,PC⊥AO于C,PD⊥OB于D,写出图中一组相等的线段______________________(只需写出一组即可)
如图,已知OE、OD分别平分∠AOB和∠BOC,若∠AOB=90°,∠EOD=70°,求∠BOC的度数.
4、如图,∠AOB=90°,OM平分∠AOB,直角三角板的顶点P在射线OM上移动,两直角边分别与OA、OB相交于点C、D,问PC与PD相等吗?试说明理由.
题型二:角平分线逆定理
1.到一个角的两边距离相等的点都在_________.
2、∠AOB的平分线上一点M,M到OA的距离为1.5 cm,则M到OB的距离为_________.
3、如图所示,表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有()
A.1处 B.2处 C.3处 D.4处
4、给出下列结论,正确的有()
①到角两边距离相等的点,在这个角的平分线上;②角的平分线与三角形平分线都是射线;③任何一个命题都有逆命题;④假命题的逆命题一定是假命题
A.1个 B.2个 C.3个 D.4个
5、已知:有一块三角形空地,若想在空地中找到一个点,使这个点到三边的距离相等,试找出该点.(保留画图痕迹)
【巩固练习】
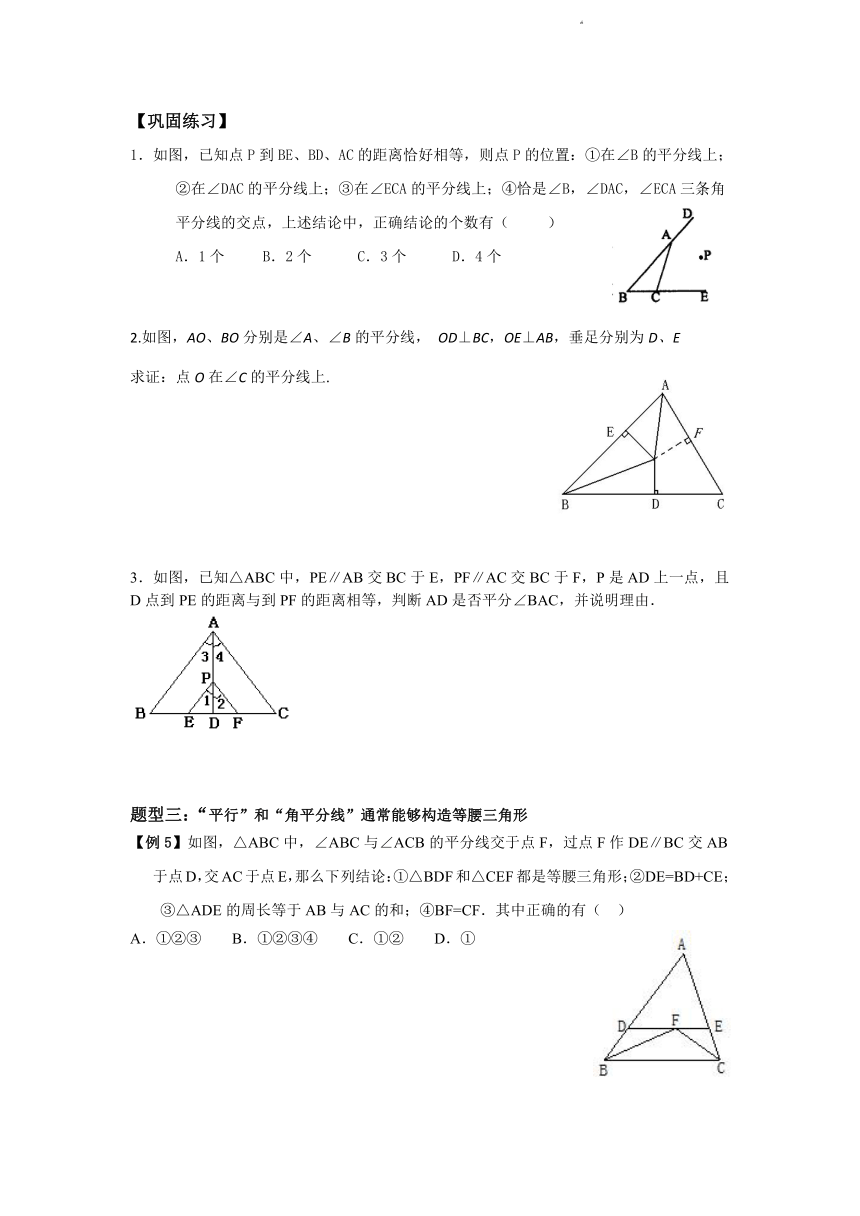
1.如图,已知点P到BE、BD、AC的距离恰好相等,则点P的位置:①在∠B的平分线上;②在∠DAC的平分线上;③在∠ECA的平分线上;④恰是∠B,∠DAC,∠ECA三条角平分线的交点,上述结论中,正确结论的个数有( )
A.1个 B.2个 C.3个 D.4个
2.如图,AO、BO分别是∠A、∠B的平分线, OD⊥BC,OE⊥AB,垂足分别为D、E
求证:点O在∠C的平分线上.
3.如图,已知△ABC中,PE∥AB交BC于E,PF∥AC交BC于F,P是AD上一点,且D点到PE的距离与到PF的距离相等,判断AD是否平分∠BAC,并说明理由.
题型三:“平行”和“角平分线”通常能够构造等腰三角形
【例5】如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长等于AB与AC的和;④BF=CF.其中正确的有( )
A.①②③ B.①②③④ C.①② D.①
【例6】如图所示,△ABC中,∠C=90°,AD平分∠A交BC于D,DE⊥AB于E,CF⊥AB于F,交AD于G.求证:DE=CG.
【巩固练习】
1.已知:如图,△ABC的外角∠FAC的平分线为AE, AD = AC。?求证:DC∥AE
题型四:角平分线性质运用
【例7】如图,在Rt△ABC中,∠C=90°,BC=AC,AD平分∠BAC交BC于D,求证:AB=AC+CD.
【例8】如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E,若△BDE的周长是4cm,求AB的长.
【巩固练习】
1.如图,CE⊥AB于E,BD⊥AC于D,BD、CE交于O,AO平分∠BAC,求证:OB=OC.
2.如图,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,BD=DC,
求证:BE=CF.
3.如图,BD是∠ABC的角平分线,DE⊥AB于点E,DF⊥BC于点F,S△ABC=36cm2,AB=18cm,BC=12cm,
求DE的长.
【例9】例:一个工厂,在公路西侧,到公路的距离与到河岸的距离相等,并且到河上公路桥头的距离为300米.在下图中标出工厂的位置,并说明理由.
【巩固练习】
1.如图所示,某铁路MN与公路PQ相交于点O,且夹角为90°,其仓库G在A区,到公路和铁路距离相等,且到铁路图上距离为1cm.
(1)在图上标出仓库G的位置.(比例尺为1∶10000,用尺规作图)
(2)求出仓库G到铁路的实际距离.
课堂达标检测
1.已知△ABC,求作一点P,使P到三角形三边的距离相等,则点P是 ( )
A.三边中垂线的交点
B.三边的高线的交点
C.三边中线的交点
D.三个内角的角平分线的交点
2.AD是△ABC的角的平分线,AB=5,AC=3,则S△ABD:S△ABD=( )
A.1:1 B.2:1 C.5:3 D.3:5
3.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=3,则PQ的最小值为( ).
A.2 B.3 C.4 D.无法确定
4.如图,直线a、b、c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
一处 B、两处 C、三处 D、四处
5.如图,在ΔABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M, 交AC于N,若BM+CN=9,则线段MN的长为( )
6 B. 7 C. 8 D. 9
6.如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB,垂足为E.若PE=3,则两平行线AD与BC间的距离为 ( )
A.3 B.5 C.6 D.不能确定
7.如图△ABC中,AD平分∠BAC,AB=4,AC=2,且△ABD的面积为3,则△ACD的面积为 .
8.已知:如图,CE⊥AB,BF⊥AC,CE与BF相交于D,且BD=CD.求证:D在∠BAC的平分线上.
