人教版七年级数学下册6.2立方根课件(35张)
文档属性
| 名称 | 人教版七年级数学下册6.2立方根课件(35张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 00:11:28 | ||
图片预览











文档简介
(共35张PPT)
1.什么叫平方根?如何用符号表示数a(≥0)
的平方根?
2.什么叫算术平方根?
如何用符号表示数a(≥0)的算术平方根?
正数a的平方根是:
正数a的算术平方根是:
正数有两个平方根,它们互为相反数;
0的平方根是0;负数没有平方根。
3.正数有几个平方根?它们之间的关系是什
么? 0平方根是什么?负数有没有平方根?
回顾 & 思考
?
1. 64的算术平方根是 ( )
2. (-6)? 的平方根是 ( )
3. 若a的平方根只有一个,那么a =( )
4.若数b 的一个平方根是1.2,那么b的另一个平方根是 ( )
5. 的算术平方根是( )
回顾 & 思考
?
1. 填空
8
6
0
-1.2
3
2.计算:
解:
2
3
±
回顾 & 思考
?
思考题
1) 一个数的两个平方根是 3a+1 与2(a-8),求这个数.
2)
6.2 立方根
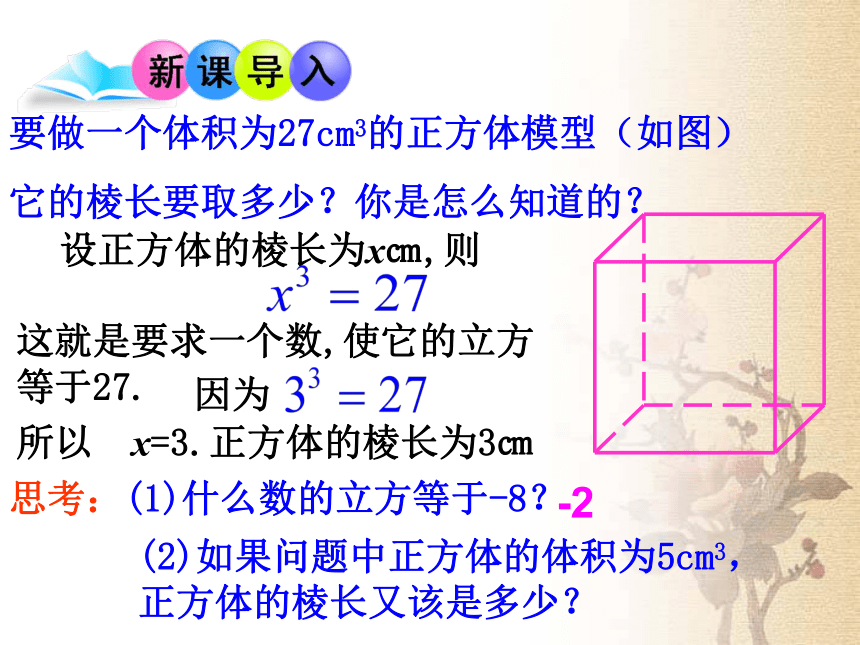
要做一个体积为27cm3的正方体模型(如图)
它的棱长要取多少?你是怎么知道的?
思考:(1)什么数的立方等于-8?
(2)如果问题中正方体的体积为5cm3,正方体的棱长又该是多少?
设正方体的棱长为x㎝,则
这就是要求一个数,使它的立方
等于27.
因为
所以 x=3.正方体的棱长为3㎝
-2
正方体的体积a
1
2
3
1
27
棱长 x
3
x
=
a
8
25
填表:
?
5
125
立方根的概念.
一般地,如果一个数的立方等于a,这个数就叫做a的立方根(也叫做三次方根).
用式子表示,如果x3 =a,那么x叫做a的立方根.
a的平方根怎样表示?
答:
或
类似的请同学们想一想a的立方根怎样表示?
立方根的表示方法:
1.立方根的概念.
一般地,如果一个数的立方等于a,这个数就叫做a的立方根(也叫做三次方根).
例如: 33=27 则把3叫做27的立方根,即
用式子表示,如果x3 =a,那么x叫做a的立方根.
数a的立方根用符号“ ”表示,
注意:根指数3不能省略.
a
3
被开方数
根指数
读作“三次根号a”
∵( )3=-8,∴ 是-8的立方根
∵( )3=1,∴ 是1的立方根
∵( )3=0,∴ 0的立方根是___
∵( )3=-64,∴ -64的立方根是___
如:23=8,则2是8的立方根
-2
立方根的表示方法.
3
a
根指数
根号
被开方数
1
1
0
0
-4
-4
-2
,
,
,
你会区别下列的数吗?
表示a的算术平方根
表示a的平方根或a的二次方根
表示a的立方根或a的三次方根
思考:
如果正方体的体积为5cm3,正方体的棱长又该是多少?
设正方体的棱长为x,则
所以正方体的棱长是
㎝.
2.开立方.
求一个数的立方根的运算,叫做开立方.
开立方与立方也是互为逆运算,因此求一个数的立方根可以通过立方运算来求.
(1)因为2 =8,所以8的立方根是( );
(2)因为( ) =0.125,所以0.125的立方是( )
(3)因为( ) =0,所以0的立方根是( );
(4)因为( ) =-8,所以-8的立方根是( );
(5)因为( ) =--,所以-- 的立方根( )
3
3
3
3
27
27
8
8
活动二 启发诱导,探索新知
2
0.5
0.5
0
0
探究题中正数、0和负数的立方根各有什么特点?
1. 探究
3
3
正数的立方根是正数
负数的立方根是负数
0的立方根是0
归 纳 总 结
正数有立方根吗?如果有,有几个?
想一想
负数呢?
零呢?
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
(1)立方根的特征
讨论:你能归纳出平方根和立方根的异同点吗?
被开方数 平方根 立方根
有两个,互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
正数
负数
零
填空:
5
5
3
例1 求下列各数的立方根
(1) 27 (2)-27 (3) (4)-0.064 (5) 0
解:
(1)∵
∴27的立方根是3
即
(2)∵
∴-27的立方根是-3
即
(3)∵
∴ 的立方根是
3
1
3
练习:1、下列说法是否正确,并说明理由
(1) 的立方根是 ( )
(2) 负数不能开立方 ( )
(3) 4的平方根是2 ( )
(4)立方根是它本身的数只有零( )
(5)平方根是它本身的数只有零( )
(6) 的立方根是4 ( )
√
×
×
×
×
×
3.求下列各数的立方根:
(1)1,(2)-1 ,(3) -0.000008 , (4)343.
练习2.填空:
-5
-5
5
4
5
4
解:
4.判断下列说法是否正确,并说明理由
x
(2) 25的平方根是5
x
(3) -64没有立方根
x
(4) -4的平方根是
x
(5) 0的平方根和立方根都是0
√
(1)
的立方根是
立方根是它本身的数有那些?
有1, -1, 0
平方根是它本身的数呢?
只有0
想一想
算术平方根是它本身的数呢?
有1, 0
因为 =____, =_____;
所以 _____
因为 =____, =_____;
所以 _____
活动四 自主探究,延伸知识
探究填空:
-2
-2
=
=
-3
-3
1.下列式子表示什么意义?你能求出它们的值吗?
?
2.分别求下列各式的值:
解:
3.计算:
4.你能求出下列各式中的未知数x吗?
(1) x3=343 (2)(x-1)3=125
解:
∴x=7
∴x-1=5
x=6
(3)
(4)
(3)
x=23
(4)
x-2=43
∴x=66
∴x=8
5.如果3x+16的立方根是4,求 2x+4的算术平方根.
6.分别求下列各式的值:
1.一个正方体的体积变为原来的8倍,其边长变为原来的多少倍?
2.一个正方体的体积变为原来的27倍,其边长变为原来的多少倍?
3.一个正方体的体积变为原来的n(n>0)倍,其边长变为原来的多少倍?
思考:
探究
先填写下表,再回答问题:
a 0.000001 0.001 1 1000 1000000
0.01
0.1
1
10
100
从上面表格中你发现什么?
被开方数的小数点向左(或向右)移动三位,那么它的立方根相应地向左(或向右)移动一位;
利用发现的规律做题
0.1442
0.01442
14.42
144.2
相同点: ①0的平方根、立方根都有一个是0
②平方根、立方根都是开方的结果。
不同点:①定义不同
②个数不同
③表示方法不同
④被开方数的取值范围不同
1.立方根的定义,性质,计算.
2.立方根与平方根的异同
小结:
1、平方根的定义:如果一个数的平方等于a,那么这个数叫做a的平方根。a的平方根用±
2、平方根的性质
(1)一个正数有两个平方根,它们互为相反数
(2)0的平方根还是0
(3)负数没有平方根
3、平方根的求法:
如求4的平方根:
∵ (±2)2 = 4
∴4的平方根是±2
即
1、立方根的定义:如果一个数的立方等于a,那么这个数叫做a的立方根。a的立方根用 表示
2、立方根的性质
(1)正数的立方根还是正数
(2)0的平方根还是0
(3)负数的立方根还是负数
3、立方根的求法:
如求8的立方根:
∵ 23 = 8
∴8的立方根是2
即
课后作业:
再见
1.什么叫平方根?如何用符号表示数a(≥0)
的平方根?
2.什么叫算术平方根?
如何用符号表示数a(≥0)的算术平方根?
正数a的平方根是:
正数a的算术平方根是:
正数有两个平方根,它们互为相反数;
0的平方根是0;负数没有平方根。
3.正数有几个平方根?它们之间的关系是什
么? 0平方根是什么?负数有没有平方根?
回顾 & 思考
?
1. 64的算术平方根是 ( )
2. (-6)? 的平方根是 ( )
3. 若a的平方根只有一个,那么a =( )
4.若数b 的一个平方根是1.2,那么b的另一个平方根是 ( )
5. 的算术平方根是( )
回顾 & 思考
?
1. 填空
8
6
0
-1.2
3
2.计算:
解:
2
3
±
回顾 & 思考
?
思考题
1) 一个数的两个平方根是 3a+1 与2(a-8),求这个数.
2)
6.2 立方根
要做一个体积为27cm3的正方体模型(如图)
它的棱长要取多少?你是怎么知道的?
思考:(1)什么数的立方等于-8?
(2)如果问题中正方体的体积为5cm3,正方体的棱长又该是多少?
设正方体的棱长为x㎝,则
这就是要求一个数,使它的立方
等于27.
因为
所以 x=3.正方体的棱长为3㎝
-2
正方体的体积a
1
2
3
1
27
棱长 x
3
x
=
a
8
25
填表:
?
5
125
立方根的概念.
一般地,如果一个数的立方等于a,这个数就叫做a的立方根(也叫做三次方根).
用式子表示,如果x3 =a,那么x叫做a的立方根.
a的平方根怎样表示?
答:
或
类似的请同学们想一想a的立方根怎样表示?
立方根的表示方法:
1.立方根的概念.
一般地,如果一个数的立方等于a,这个数就叫做a的立方根(也叫做三次方根).
例如: 33=27 则把3叫做27的立方根,即
用式子表示,如果x3 =a,那么x叫做a的立方根.
数a的立方根用符号“ ”表示,
注意:根指数3不能省略.
a
3
被开方数
根指数
读作“三次根号a”
∵( )3=-8,∴ 是-8的立方根
∵( )3=1,∴ 是1的立方根
∵( )3=0,∴ 0的立方根是___
∵( )3=-64,∴ -64的立方根是___
如:23=8,则2是8的立方根
-2
立方根的表示方法.
3
a
根指数
根号
被开方数
1
1
0
0
-4
-4
-2
,
,
,
你会区别下列的数吗?
表示a的算术平方根
表示a的平方根或a的二次方根
表示a的立方根或a的三次方根
思考:
如果正方体的体积为5cm3,正方体的棱长又该是多少?
设正方体的棱长为x,则
所以正方体的棱长是
㎝.
2.开立方.
求一个数的立方根的运算,叫做开立方.
开立方与立方也是互为逆运算,因此求一个数的立方根可以通过立方运算来求.
(1)因为2 =8,所以8的立方根是( );
(2)因为( ) =0.125,所以0.125的立方是( )
(3)因为( ) =0,所以0的立方根是( );
(4)因为( ) =-8,所以-8的立方根是( );
(5)因为( ) =--,所以-- 的立方根( )
3
3
3
3
27
27
8
8
活动二 启发诱导,探索新知
2
0.5
0.5
0
0
探究题中正数、0和负数的立方根各有什么特点?
1. 探究
3
3
正数的立方根是正数
负数的立方根是负数
0的立方根是0
归 纳 总 结
正数有立方根吗?如果有,有几个?
想一想
负数呢?
零呢?
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
(1)立方根的特征
讨论:你能归纳出平方根和立方根的异同点吗?
被开方数 平方根 立方根
有两个,互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
正数
负数
零
填空:
5
5
3
例1 求下列各数的立方根
(1) 27 (2)-27 (3) (4)-0.064 (5) 0
解:
(1)∵
∴27的立方根是3
即
(2)∵
∴-27的立方根是-3
即
(3)∵
∴ 的立方根是
3
1
3
练习:1、下列说法是否正确,并说明理由
(1) 的立方根是 ( )
(2) 负数不能开立方 ( )
(3) 4的平方根是2 ( )
(4)立方根是它本身的数只有零( )
(5)平方根是它本身的数只有零( )
(6) 的立方根是4 ( )
√
×
×
×
×
×
3.求下列各数的立方根:
(1)1,(2)-1 ,(3) -0.000008 , (4)343.
练习2.填空:
-5
-5
5
4
5
4
解:
4.判断下列说法是否正确,并说明理由
x
(2) 25的平方根是5
x
(3) -64没有立方根
x
(4) -4的平方根是
x
(5) 0的平方根和立方根都是0
√
(1)
的立方根是
立方根是它本身的数有那些?
有1, -1, 0
平方根是它本身的数呢?
只有0
想一想
算术平方根是它本身的数呢?
有1, 0
因为 =____, =_____;
所以 _____
因为 =____, =_____;
所以 _____
活动四 自主探究,延伸知识
探究填空:
-2
-2
=
=
-3
-3
1.下列式子表示什么意义?你能求出它们的值吗?
?
2.分别求下列各式的值:
解:
3.计算:
4.你能求出下列各式中的未知数x吗?
(1) x3=343 (2)(x-1)3=125
解:
∴x=7
∴x-1=5
x=6
(3)
(4)
(3)
x=23
(4)
x-2=43
∴x=66
∴x=8
5.如果3x+16的立方根是4,求 2x+4的算术平方根.
6.分别求下列各式的值:
1.一个正方体的体积变为原来的8倍,其边长变为原来的多少倍?
2.一个正方体的体积变为原来的27倍,其边长变为原来的多少倍?
3.一个正方体的体积变为原来的n(n>0)倍,其边长变为原来的多少倍?
思考:
探究
先填写下表,再回答问题:
a 0.000001 0.001 1 1000 1000000
0.01
0.1
1
10
100
从上面表格中你发现什么?
被开方数的小数点向左(或向右)移动三位,那么它的立方根相应地向左(或向右)移动一位;
利用发现的规律做题
0.1442
0.01442
14.42
144.2
相同点: ①0的平方根、立方根都有一个是0
②平方根、立方根都是开方的结果。
不同点:①定义不同
②个数不同
③表示方法不同
④被开方数的取值范围不同
1.立方根的定义,性质,计算.
2.立方根与平方根的异同
小结:
1、平方根的定义:如果一个数的平方等于a,那么这个数叫做a的平方根。a的平方根用±
2、平方根的性质
(1)一个正数有两个平方根,它们互为相反数
(2)0的平方根还是0
(3)负数没有平方根
3、平方根的求法:
如求4的平方根:
∵ (±2)2 = 4
∴4的平方根是±2
即
1、立方根的定义:如果一个数的立方等于a,那么这个数叫做a的立方根。a的立方根用 表示
2、立方根的性质
(1)正数的立方根还是正数
(2)0的平方根还是0
(3)负数的立方根还是负数
3、立方根的求法:
如求8的立方根:
∵ 23 = 8
∴8的立方根是2
即
课后作业:
再见
