2020春北师大版八下数学第5章分式与分式方程同步练习(4课时 含答案)
文档属性
| 名称 | 2020春北师大版八下数学第5章分式与分式方程同步练习(4课时 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 59.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 00:20:07 | ||
图片预览



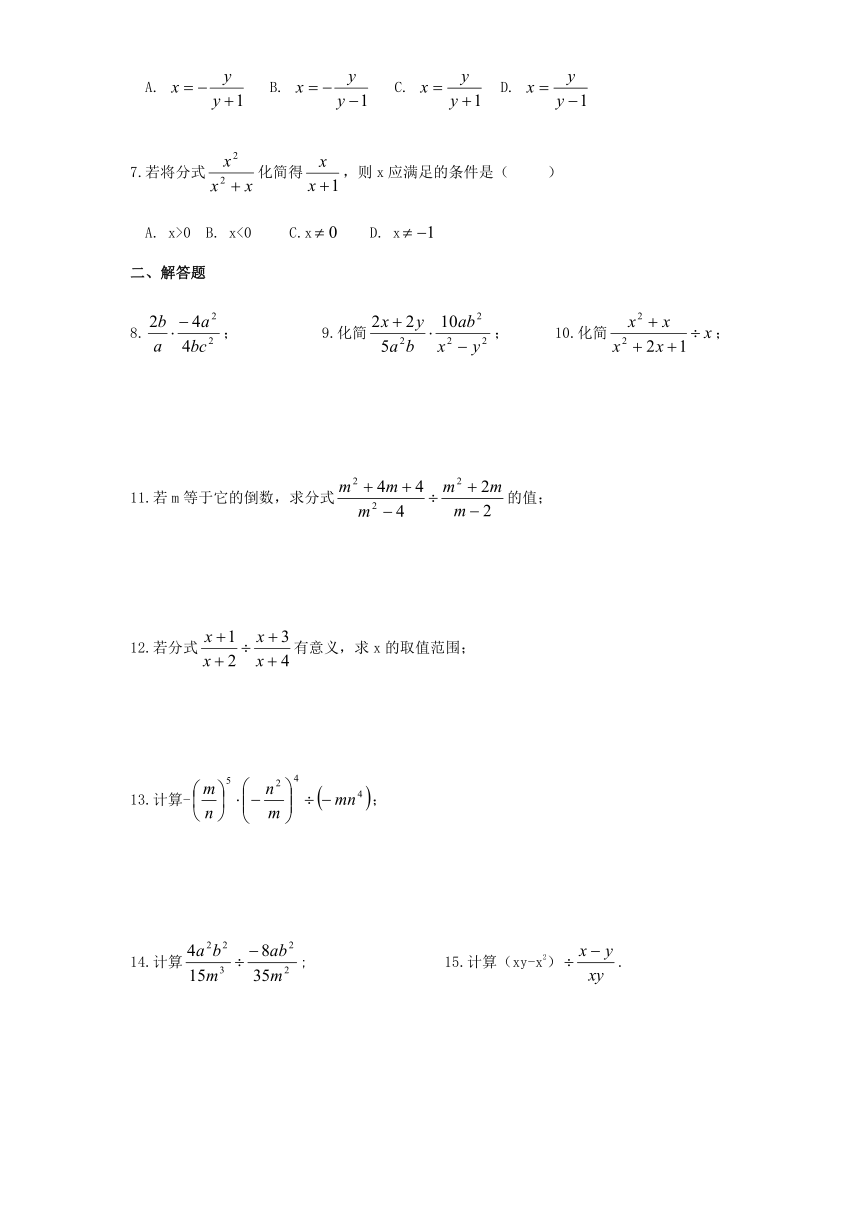
文档简介
2020春北师大版八下数学第5章分式与分式方程同步练习及答案
5.1认识分式
1.下列说法正确的是( )
A.如果A,B是整式,那么就叫做分式;
B.只要分式的分子为零,则分式的值就为零;
C.只要分式的分母为零,则分式必无意义;
D.因为不是分式,而是整式.
2.在,,,,a+中,分式的个数有( )
A. 2个 B. 3个 C. 4个 D. 5个
3.使分式有意义的a取值应是( )
A. 任意实数 B. a C. a D. a或1
4.要使分式有意义,则a取值应是( )
A.-1 B. 1 C. D. 任意实数
5.当x=2时,下列各式的值为0的是( )
A. B. C. D.
6.对于分式中,当x=-a时,下列结论正确地是( )
A. 分式无意义 B. 分式值为0
C. 当a时,分式的值为0 D. 当a时,分式的值为0
7.下列各式从左到右的变形不正确的是( )
A.. B. C. D.
8.下列各个算式中正确的是( )
A.;B. ;C. ;D.
9.把分式( )
A.扩大4倍 B.扩大2倍 C. 缩小2倍 D. 不变
10.下列等式成立的是( )
A. B
C. D
11.在-3x,中,是分式的是 .
12.要使分式 有意义,则a的值应是 ;要使分式的值为零,则a的值应为 .
13.分式,当 时,其值为0;当 时,分式无意义;当 时,分式的值为正数.
14,化简 .
15,当x=3时,分式的值为 .
参考答案:
1.C 2B 3C 4D 5C 6C 7D 8D 9D 10B 11
12 a a=2 13 x=0 x= -114 15. 5
5.2分式的乘除法
一、选择题
1.下列运算正确的是( )
A. B. C. D.
2.下列分式运算,结果正确的是( )
A.; B. C . ; D.
3.已知a-b,且2a-3b=0,则代数式的值是( )
A.-12 B.0 C.4 D.4或-12
4.已知,则的值是( )
A. B. C. D.
5.化简x等于( )
A.1 B.xy C. D.
6.如果y=,那么用y的代数式表示x为( )
A. B. C. D.
7.若将分式化简得,则x应满足的条件是( )
A. x>0 B. x<0 C.x D. x
二、解答题
8.; 9.化简; 10.化简;
11.若m等于它的倒数,求分式的值;
12.若分式有意义,求x的取值范围;
13.计算-;
14.计算; 15.计算(xy-x2).
参考答案:
1. C 2 .A 3.C 4.C 5.C 6.D 7.C
8.- 9. 10. 11.
12. 13. 14.- 15.-
5.3分式的加减法
1.已知x,则等于( )
A. B. C. D.
2.化简可得到( )
A.零 B.零次多项式 C.一次多项式 D.不为零的分式
3.分式的最简公分母是( )
A.5abx B.15ab C.15abx D.15ab
4.在分式①②;③④中分母相同的分式是( )A.①③④ B.②③ C.②④ D.①③
5.下列算式中正确的是( )
A.; B.; C.; D.
6.x 克盐溶解在a克水中,取这种盐水m克,其中含盐( )
A.克 B.克 C.克 D.克
7. ;
8. ;
9.若ab=2,a+b=-1,则 的值为 ;
10.计算 ;
11.化简分式的结果是 ;
12.计算:
(1); (2);
13.化简;
14.先化简,再求值:其中x=-3.5.
15.先化简,再求值:,其中x=+1.
参考答案:
1.D 2.A 3.D 4.C 5.D 6.D 7.–1 8. 9.- 10.
11. x2-y2
12.(1)原式=;
(2)原式=.
13.原式=.
14.原式=,当x=-3.5时,原式的值为-.
15.原式=
当x=+1时,原式的值为.
5.4分式方程
1.判断下列各题,正确的在题后括号内打“√”,错误的打“×”.
(1)=是关于y的分式方程. ( )
(2)分式方程=0的解是x=3. ( )
(3)只要是分式方程,一定出现增根. ( )
(4)方程=与方程5(x-2)=7x的解相同. ( )
(5)方程 =-3的两边都乘以(x-2),得1=(x-1)-3. ( )
(6)方程=-3无解. ( )
(7)方程=的根为x=0. ( )
(8)方程变形得x=1,而x=1是原方程的增根,故原方程无解.( )
2.若的值为-1,则x等于 ( )
A.- B. C. D.-
3.老张师傅做m个零件用了一个小时,则他做20个零件需要的小时数是 ( )
A. B. C.20m D.20+m
4.一项工程,甲独做需m小时完成,若与乙合作20小时完成,则乙单独完成需要的时间是( )
A. B. C. D.
5.甲、乙两班学生参加植树造林,已知甲班每天比乙班多植5棵树,甲班植80棵树所用的天数与乙班植70棵树所用的天数想等,若设甲班每天植树x棵,则根据题意列出的方程是( )
A.= B. C. D.
6.下列各式中,不是分式方程的是( )
A. B. C. D.·(
7.分式方程+的解是 ( )
A.无解 B.x=2 C.x=-3 D.x=±3
8.若分式方程无解,则a的值是 ( )
A.-1 B. 1 C. ±1 D.-2
9.若分式方程(其中k为常数)产生增根,则增根是 ( )
A.x=6 B.x=5 C.x=k D.无法确定
10.解关于x的方程产生增根,则常数m的值等于 ( )
A.-2 B.-1 C.1 D.2
11.下列关于x的方程①,②,③1,④中,是分式方程的是 ( )(填序号)
12.如果,则x= .
13.方程的解是 .
14.甲做90个机器零件所用的时间与乙做120个机器零件所用的时间相等,又已知平均每小时甲、乙两人一共做了35个零件,求甲、乙每小时各做多少个?
15.某校师生到距学校20千米的公路旁植树,甲班师生骑自行车先走,45分钟后,乙班师生乘汽车出发,结果两班师生同时到达,已知汽车的速度是自行车速度的2.5倍,求两种车的速度各是多少?
参考答案:
1.(1)×;(2)×;(3)×;(4)√;
(5)× 提示:去分母时,漏掉了-3这一项,应改为1=(x-1)-3(x-2);
(6)√;(7) ×;(8) ×.
2.C 3.B 4.A 5.D 6.D 7.B 8.C 9.C
10.A 11.② 12.-3
13.x=0
14.设甲每小时做x个,则乙每小时做(35-x)个,由题意可列方程为.
解得x=15,经检验x=15适合题意,故甲每小时做15个,乙每小时做20个.
15.设自行车速度为x千米/小时,则汽车速度为2.5x千米/小时,
由题意可列方程为,解得x=16,经检验,x=16适合题意,
故2.5x=40,所以自行车速度为16千米/小时,汽车速度为40千米/小时.
5.1认识分式
1.下列说法正确的是( )
A.如果A,B是整式,那么就叫做分式;
B.只要分式的分子为零,则分式的值就为零;
C.只要分式的分母为零,则分式必无意义;
D.因为不是分式,而是整式.
2.在,,,,a+中,分式的个数有( )
A. 2个 B. 3个 C. 4个 D. 5个
3.使分式有意义的a取值应是( )
A. 任意实数 B. a C. a D. a或1
4.要使分式有意义,则a取值应是( )
A.-1 B. 1 C. D. 任意实数
5.当x=2时,下列各式的值为0的是( )
A. B. C. D.
6.对于分式中,当x=-a时,下列结论正确地是( )
A. 分式无意义 B. 分式值为0
C. 当a时,分式的值为0 D. 当a时,分式的值为0
7.下列各式从左到右的变形不正确的是( )
A.. B. C. D.
8.下列各个算式中正确的是( )
A.;B. ;C. ;D.
9.把分式( )
A.扩大4倍 B.扩大2倍 C. 缩小2倍 D. 不变
10.下列等式成立的是( )
A. B
C. D
11.在-3x,中,是分式的是 .
12.要使分式 有意义,则a的值应是 ;要使分式的值为零,则a的值应为 .
13.分式,当 时,其值为0;当 时,分式无意义;当 时,分式的值为正数.
14,化简 .
15,当x=3时,分式的值为 .
参考答案:
1.C 2B 3C 4D 5C 6C 7D 8D 9D 10B 11
12 a a=2 13 x=0 x= -1
5.2分式的乘除法
一、选择题
1.下列运算正确的是( )
A. B. C. D.
2.下列分式运算,结果正确的是( )
A.; B. C . ; D.
3.已知a-b,且2a-3b=0,则代数式的值是( )
A.-12 B.0 C.4 D.4或-12
4.已知,则的值是( )
A. B. C. D.
5.化简x等于( )
A.1 B.xy C. D.
6.如果y=,那么用y的代数式表示x为( )
A. B. C. D.
7.若将分式化简得,则x应满足的条件是( )
A. x>0 B. x<0 C.x D. x
二、解答题
8.; 9.化简; 10.化简;
11.若m等于它的倒数,求分式的值;
12.若分式有意义,求x的取值范围;
13.计算-;
14.计算; 15.计算(xy-x2).
参考答案:
1. C 2 .A 3.C 4.C 5.C 6.D 7.C
8.- 9. 10. 11.
12. 13. 14.- 15.-
5.3分式的加减法
1.已知x,则等于( )
A. B. C. D.
2.化简可得到( )
A.零 B.零次多项式 C.一次多项式 D.不为零的分式
3.分式的最简公分母是( )
A.5abx B.15ab C.15abx D.15ab
4.在分式①②;③④中分母相同的分式是( )A.①③④ B.②③ C.②④ D.①③
5.下列算式中正确的是( )
A.; B.; C.; D.
6.x 克盐溶解在a克水中,取这种盐水m克,其中含盐( )
A.克 B.克 C.克 D.克
7. ;
8. ;
9.若ab=2,a+b=-1,则 的值为 ;
10.计算 ;
11.化简分式的结果是 ;
12.计算:
(1); (2);
13.化简;
14.先化简,再求值:其中x=-3.5.
15.先化简,再求值:,其中x=+1.
参考答案:
1.D 2.A 3.D 4.C 5.D 6.D 7.–1 8. 9.- 10.
11. x2-y2
12.(1)原式=;
(2)原式=.
13.原式=.
14.原式=,当x=-3.5时,原式的值为-.
15.原式=
当x=+1时,原式的值为.
5.4分式方程
1.判断下列各题,正确的在题后括号内打“√”,错误的打“×”.
(1)=是关于y的分式方程. ( )
(2)分式方程=0的解是x=3. ( )
(3)只要是分式方程,一定出现增根. ( )
(4)方程=与方程5(x-2)=7x的解相同. ( )
(5)方程 =-3的两边都乘以(x-2),得1=(x-1)-3. ( )
(6)方程=-3无解. ( )
(7)方程=的根为x=0. ( )
(8)方程变形得x=1,而x=1是原方程的增根,故原方程无解.( )
2.若的值为-1,则x等于 ( )
A.- B. C. D.-
3.老张师傅做m个零件用了一个小时,则他做20个零件需要的小时数是 ( )
A. B. C.20m D.20+m
4.一项工程,甲独做需m小时完成,若与乙合作20小时完成,则乙单独完成需要的时间是( )
A. B. C. D.
5.甲、乙两班学生参加植树造林,已知甲班每天比乙班多植5棵树,甲班植80棵树所用的天数与乙班植70棵树所用的天数想等,若设甲班每天植树x棵,则根据题意列出的方程是( )
A.= B. C. D.
6.下列各式中,不是分式方程的是( )
A. B. C. D.·(
7.分式方程+的解是 ( )
A.无解 B.x=2 C.x=-3 D.x=±3
8.若分式方程无解,则a的值是 ( )
A.-1 B. 1 C. ±1 D.-2
9.若分式方程(其中k为常数)产生增根,则增根是 ( )
A.x=6 B.x=5 C.x=k D.无法确定
10.解关于x的方程产生增根,则常数m的值等于 ( )
A.-2 B.-1 C.1 D.2
11.下列关于x的方程①,②,③1,④中,是分式方程的是 ( )(填序号)
12.如果,则x= .
13.方程的解是 .
14.甲做90个机器零件所用的时间与乙做120个机器零件所用的时间相等,又已知平均每小时甲、乙两人一共做了35个零件,求甲、乙每小时各做多少个?
15.某校师生到距学校20千米的公路旁植树,甲班师生骑自行车先走,45分钟后,乙班师生乘汽车出发,结果两班师生同时到达,已知汽车的速度是自行车速度的2.5倍,求两种车的速度各是多少?
参考答案:
1.(1)×;(2)×;(3)×;(4)√;
(5)× 提示:去分母时,漏掉了-3这一项,应改为1=(x-1)-3(x-2);
(6)√;(7) ×;(8) ×.
2.C 3.B 4.A 5.D 6.D 7.B 8.C 9.C
10.A 11.② 12.-3
13.x=0
14.设甲每小时做x个,则乙每小时做(35-x)个,由题意可列方程为.
解得x=15,经检验x=15适合题意,故甲每小时做15个,乙每小时做20个.
15.设自行车速度为x千米/小时,则汽车速度为2.5x千米/小时,
由题意可列方程为,解得x=16,经检验,x=16适合题意,
故2.5x=40,所以自行车速度为16千米/小时,汽车速度为40千米/小时.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
