华师大版初中数学七年级下册第7章一次方程组章末复习课件(38张PPT)
文档属性
| 名称 | 华师大版初中数学七年级下册第7章一次方程组章末复习课件(38张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 603.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-29 09:40:45 | ||
图片预览











文档简介
课件38张PPT。章末复习
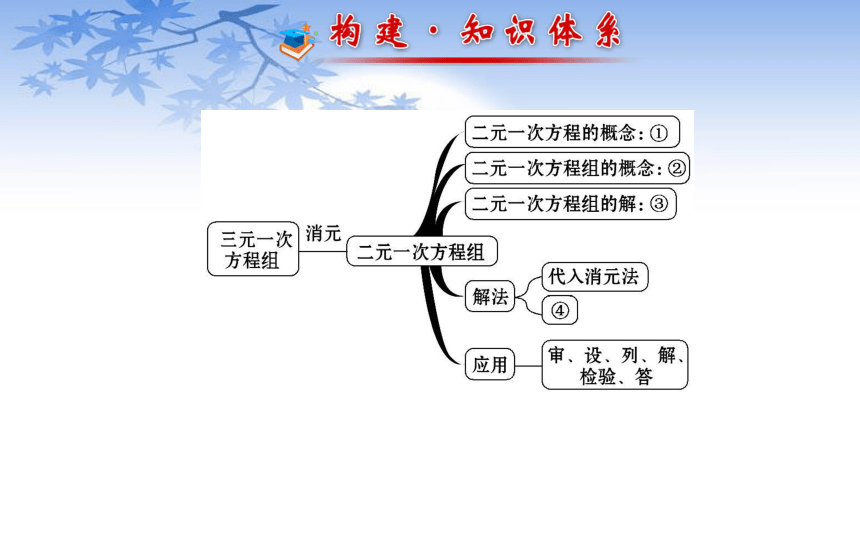
第 7 章请写出框图中数字处的内容:
①________________________________________________;
②_________________________________________;
③___________________________________________________
_____________;
④___________.有两个未知数,并且含未知数的项的次数都是1的方程含有相同未知数的两个二元一次方程合在一起使二元一次方程组中两个方程的左右两边的值都相等的两个未知数的值加减消元法考点 1 二元一次方程(组)及解
【知识点睛】
1.二元一次方程的定义及解常考查的知识点:
(1)未知数的个数(2个)、系数(不为0)和次数(未知数的次数是1),以此判断一个方程是不是二元一次方程.
(2)由于二元一次方程有无数组解,确定其整数解是中考中的常考题型.2.二元一次方程组及解的主要题型:
(1)给出几组值,判断是不是方程组的解,通常用检验的办法判断.
(2)已知方程组的解求方程组中未知数的系数,常以填空题和选择题的题型出现,一般用代入的办法求解.【例1】关于x,y的方程组
的解是 则|m-n|的值是( )
A.5 B.3 C.2 D.1
【思路点拨】将x,y的值代入方程组,求出m,n的值,再计算得出|m-n|的值.【自主解答】选D.将 代入
得 解得
所以|m-n|=|2-3|=1.【中考集训】
1.方程2x-y=1和2x+y=7的公共解是( )
【解析】选D.把A,B,C,D分别代入已知的两个方程验证即可.2.如果4xa+2b-5-2y3a-b-3=8是二元一次方程,
那么a-b=_______.
【解析】因为4xa+2b-5-2y3a-b-3=8是二元一次方程,所以有
解得 所以a-b=0.
答案:03.已知关于x,y的方程组 的解
为 求m,n的值.
【解析】把 代入 得
解得:考点 2 二元一次方程组的解法
【知识点睛】
1.解二元一次方程组的常用方法:
(1)代入消元法:需要用含有一个未知数的代数式表示另一个未知数,这也就是说当方程的系数比较简单时,用这种方法比较方便.
(2)整体代入法:如果系数存在整数倍数关系时,可以把系数较小的一项的系数与未知数看作一个整体来变形.(3)加减消元法:当二元一次方程组中两个方程的同一个未知数的系数相等或互为相反数时,把两个方程直接相减或相加,就可以消去一个未知数.
(4)先取最小公倍数再用加减消元法:当各个未知数的系数既不相等又不互为相反数时,可以观察一下看哪一个未知数的系数的最小公倍数小,然后把方程变形,再用加减消元法.2.选择消元的方法:
(1)当方程组中有一个方程的某一个未知数的系数的绝对值是1或者有一个方程的常数项是0时,考虑用代入法.
(2)当两个方程的某一个未知数的系数的绝对值相等或者成整数倍时,用加减法比较简单.【例2】解方程组:
【思路点拨】 方法一:将②变形为用y表示
x的形式,再代入①,求出y,进而求出x.
方法二:②×4+①消去y,求出x,再代入②求出y.【自主解答】方法一:
由②,得x=4+y③,
把③代入①,得3(4+y)+4y=19,
12+3y+4y=19,y=1.
把y=1代入③,得x=4+1=5.
所以方程组的解为
方法二:
②×4+①得7x=35,解得x=5.
代入②得y=1,所以方程组的解为【中考集训】
1.已知 则a+b等于( )
A.3 B. C.2 D.1
【解析】选A.两个方程相加,得4a+4b=12,所以a+b=3.2.由方程组 可得出x与y的关系式
是( )
A.x+y=9 B.x+y=3
C.x+y=-3 D.x+y=-9
【解析】选A.把y-3=m代入x+m=6得,x+y-3=6,移项,得x+y=9.3.已知 是关于x,y的二元一次方程组
的解,则a+b=_______.
【解析】把 代入方程组 得
解方程组得 故a+b=
答案:4.解方程组
【解析】①+②,得3x=6,所以x=2.
把x=2代入①,得2+y=1,所以y=-1.
所以方程组的解为【知识拓展】用换元法解方程组
(1)直接换元:当题中两个方程所含未知数的式子结构类似时,可针对两个式子进行直接换元,得到两个简单的二元一次方程组,解得这个方程组后,再代入所设两个式子,求得原变元方程组的解,从而降低了解题的难度,达到易解的目的.(2)整体换元:利用系数之间成倍数关系,将方程组中相同的
整式用新的未知数表示,变复杂形式为简单形式.例如,解方
程组 由②,得2(3x+4y)+y=12,设3x+4y=t,
原方程组变为 解得 即
解得 即这个方程组的解是5.解方程组:
【解析】方法一:①+②,得 3x=6,所以x=2.
把x=2代入①,得 2+y=5,所以y=3.所以
方法二:由①,得 y=5-x③.把③代入②,得 2x-(5-x)
=1,解得x=2.把x=2代入③,得 y=3.所以考点 3 二元一次方程组在实际问题中的应用
【知识点睛】
用二元一次方程组解决实际问题,是各地中考考查的重点内容之一.解决此类问题的步骤是审、设、列、解、答,关键是找出题目中的两(三)个相等关系,并把已知量和未知量通过相等关系联系起来,列出方程组求解.最后要准确判断方程组的解是否符合题意并正确作答.【例3】某寄宿制学校有大、小两种类型的学生宿舍共50间,大宿舍每间可住8人,小宿舍每间可住6人.该校360名住宿生恰好住满这50间宿舍.求大、小宿舍各有多少间.
【思路点拨】本题中的两个等量关系分别为:
①大、小宿舍共50间.
②共360名住宿生恰好住满这50间宿舍.
根据等量关系列出方程组求解.【自主解答】设大宿舍有x间,小宿舍有y间,根据题意得
解得
答:大宿舍有30间,小宿舍有20间.【中考集训】
1.甲、乙二人在一环形场地上从A点同时同向匀速跑步,甲的速度是乙的2.5倍,4分钟两人首次相遇,此时乙还需要跑300米才跑完第一圈,求甲、乙二人的速度及环形场地的周长.(列方程组求解)【解析】设乙的速度为x米/分,
则甲的速度为2.5x米/分,环形场地的周长为y米,
由题意,得 解得:
∴甲的速度为:2.5×150=375米/分.
答:乙的速度为150米/分,甲的速度为375米/分,环形场地的周长为900米.2.为方便市民出行,减轻城市中心交通压力,长沙市正在修建贯穿星城南北、东西的地铁1,2号线.已知修建地铁1号线24千米和2号线22千米共需投资265亿元;若1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.
(1)求1号线,2号线每千米的平均造价分别是多少亿元?
(2)除1,2号线外,长沙市政府规划到2018年还需再建91.8千米的地铁线网.据预算,这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍,则还需投资多少亿元?【解析】(1)设1号线每千米的平均造价为x亿元,2号线每千
米的平均造价为y亿元,由题意得:
解得
答:1,2号线每千米的平均造价分别为6亿元、5.5亿元.
(2)91.8×6×1.2=660.96(亿元).
答:还需投资660.96亿元.3.某镇水库的可用水量为12 000万立方米,假设年降水量不变,能维持该镇16万人20年的用水量.实施城市化建设,新迁入4万人后,水库只够维持居民15年的用水量.
(1)问:年降水量为多少万立方米?每人年平均用水量多少立方米?
(2)政府号召节约用水,希望将水库的保用年限提高到25年,则该镇居民人均每年需节约多少立方米才能实现目标? 【解析】(1)设年降水量为x万立方米,每人年平均用水量为
y立方米,则: 解得:
答:年降水量为200万立方米,每人年平均用水量为50立方米.
(2)设该城镇居民年平均用水量为z立方米才能实现目标,则:
12 000+25×200=20×25z,解得:z=34.
∴50-34=16.
答:该城镇居民人均每年需要节约16立方米的水才能实现目标.4.用一根绳子绕一个圆柱形油桶.若环绕油
桶3周,则绳子还多4尺;若环绕油桶4周,则绳子又少了3尺.
这根绳子有多长?环绕油桶一周需要多少尺?
【解析】设这根绳子长为x尺,环绕油桶一周需y尺,由题意,
得 解得
答:这根绳子长为25尺,环绕油桶一周需7尺.5.为了进一步推进海南国际旅游岛建设,海口市自2012年4月1日起实施《海口市奖励旅行社开发客源市场暂行办法》,第八条规定:旅行社引进会议规模达到200人以上,入住本市A类旅游饭店,每次会议奖励2万元;入住本市B类旅游饭店,每次会议奖励1万元.某旅行社5月份引进符合奖励规定的会议18次,得到28万元奖金.求此旅行社引进符合奖励规定的入住A类和B类旅游饭店的会议各多少次.【解析】设入住A类旅游饭店的会议x次,入住B类旅游饭店的
会议y次.
根据题意,得 解得
答:此旅行社引进符合奖励规定的入住A类旅游饭店的会议
10次,入住B类旅游饭店的会议8次.【知识拓展】巧用“设而不求”化解问题
“设而不求”,顾名思义是除了设要求的未知数外,再多设另外一些相关的未知数作为辅助未知数,以便把已知和未知联系起来,易于建立方程(组),然后在解方程或方程组时,不必考虑辅助未知数的求解,只需直接考虑问题的解.请看:【例】某游泳选手携带一空水壶(可漂浮的)沿河逆流练习游泳,于A处不小心把水壶遗失,在他继续往前游了30分钟后才发现,于是立即返回追赶,结果在距离A处3千米的下游处追回.问河水的流速是多少?【解析】本题中除了所求的水流速度外,还有游泳者的速度、追赶水壶的时间.只有这些未知量都参与才能轻易地列出方程组.因此,除了设水流速度为x千米/时外,还需再设游泳者在静水中的速度为a千米/时,追赶水壶的时间为b小时,则依题意,有
①代入②,得(b+0.5)x=ab+bx-0.5a+0.5x, ③
所以0.5a=ab,
因为a≠0,所以b=0.5,从而由②得x=3.“设而不求”是解较高难度应用题的一种技巧,这种技巧源自方程组思想,当问题的已知条件给人一种感觉很少或“不足”时,“设而不求”将大显身手.
第 7 章请写出框图中数字处的内容:
①________________________________________________;
②_________________________________________;
③___________________________________________________
_____________;
④___________.有两个未知数,并且含未知数的项的次数都是1的方程含有相同未知数的两个二元一次方程合在一起使二元一次方程组中两个方程的左右两边的值都相等的两个未知数的值加减消元法考点 1 二元一次方程(组)及解
【知识点睛】
1.二元一次方程的定义及解常考查的知识点:
(1)未知数的个数(2个)、系数(不为0)和次数(未知数的次数是1),以此判断一个方程是不是二元一次方程.
(2)由于二元一次方程有无数组解,确定其整数解是中考中的常考题型.2.二元一次方程组及解的主要题型:
(1)给出几组值,判断是不是方程组的解,通常用检验的办法判断.
(2)已知方程组的解求方程组中未知数的系数,常以填空题和选择题的题型出现,一般用代入的办法求解.【例1】关于x,y的方程组
的解是 则|m-n|的值是( )
A.5 B.3 C.2 D.1
【思路点拨】将x,y的值代入方程组,求出m,n的值,再计算得出|m-n|的值.【自主解答】选D.将 代入
得 解得
所以|m-n|=|2-3|=1.【中考集训】
1.方程2x-y=1和2x+y=7的公共解是( )
【解析】选D.把A,B,C,D分别代入已知的两个方程验证即可.2.如果4xa+2b-5-2y3a-b-3=8是二元一次方程,
那么a-b=_______.
【解析】因为4xa+2b-5-2y3a-b-3=8是二元一次方程,所以有
解得 所以a-b=0.
答案:03.已知关于x,y的方程组 的解
为 求m,n的值.
【解析】把 代入 得
解得:考点 2 二元一次方程组的解法
【知识点睛】
1.解二元一次方程组的常用方法:
(1)代入消元法:需要用含有一个未知数的代数式表示另一个未知数,这也就是说当方程的系数比较简单时,用这种方法比较方便.
(2)整体代入法:如果系数存在整数倍数关系时,可以把系数较小的一项的系数与未知数看作一个整体来变形.(3)加减消元法:当二元一次方程组中两个方程的同一个未知数的系数相等或互为相反数时,把两个方程直接相减或相加,就可以消去一个未知数.
(4)先取最小公倍数再用加减消元法:当各个未知数的系数既不相等又不互为相反数时,可以观察一下看哪一个未知数的系数的最小公倍数小,然后把方程变形,再用加减消元法.2.选择消元的方法:
(1)当方程组中有一个方程的某一个未知数的系数的绝对值是1或者有一个方程的常数项是0时,考虑用代入法.
(2)当两个方程的某一个未知数的系数的绝对值相等或者成整数倍时,用加减法比较简单.【例2】解方程组:
【思路点拨】 方法一:将②变形为用y表示
x的形式,再代入①,求出y,进而求出x.
方法二:②×4+①消去y,求出x,再代入②求出y.【自主解答】方法一:
由②,得x=4+y③,
把③代入①,得3(4+y)+4y=19,
12+3y+4y=19,y=1.
把y=1代入③,得x=4+1=5.
所以方程组的解为
方法二:
②×4+①得7x=35,解得x=5.
代入②得y=1,所以方程组的解为【中考集训】
1.已知 则a+b等于( )
A.3 B. C.2 D.1
【解析】选A.两个方程相加,得4a+4b=12,所以a+b=3.2.由方程组 可得出x与y的关系式
是( )
A.x+y=9 B.x+y=3
C.x+y=-3 D.x+y=-9
【解析】选A.把y-3=m代入x+m=6得,x+y-3=6,移项,得x+y=9.3.已知 是关于x,y的二元一次方程组
的解,则a+b=_______.
【解析】把 代入方程组 得
解方程组得 故a+b=
答案:4.解方程组
【解析】①+②,得3x=6,所以x=2.
把x=2代入①,得2+y=1,所以y=-1.
所以方程组的解为【知识拓展】用换元法解方程组
(1)直接换元:当题中两个方程所含未知数的式子结构类似时,可针对两个式子进行直接换元,得到两个简单的二元一次方程组,解得这个方程组后,再代入所设两个式子,求得原变元方程组的解,从而降低了解题的难度,达到易解的目的.(2)整体换元:利用系数之间成倍数关系,将方程组中相同的
整式用新的未知数表示,变复杂形式为简单形式.例如,解方
程组 由②,得2(3x+4y)+y=12,设3x+4y=t,
原方程组变为 解得 即
解得 即这个方程组的解是5.解方程组:
【解析】方法一:①+②,得 3x=6,所以x=2.
把x=2代入①,得 2+y=5,所以y=3.所以
方法二:由①,得 y=5-x③.把③代入②,得 2x-(5-x)
=1,解得x=2.把x=2代入③,得 y=3.所以考点 3 二元一次方程组在实际问题中的应用
【知识点睛】
用二元一次方程组解决实际问题,是各地中考考查的重点内容之一.解决此类问题的步骤是审、设、列、解、答,关键是找出题目中的两(三)个相等关系,并把已知量和未知量通过相等关系联系起来,列出方程组求解.最后要准确判断方程组的解是否符合题意并正确作答.【例3】某寄宿制学校有大、小两种类型的学生宿舍共50间,大宿舍每间可住8人,小宿舍每间可住6人.该校360名住宿生恰好住满这50间宿舍.求大、小宿舍各有多少间.
【思路点拨】本题中的两个等量关系分别为:
①大、小宿舍共50间.
②共360名住宿生恰好住满这50间宿舍.
根据等量关系列出方程组求解.【自主解答】设大宿舍有x间,小宿舍有y间,根据题意得
解得
答:大宿舍有30间,小宿舍有20间.【中考集训】
1.甲、乙二人在一环形场地上从A点同时同向匀速跑步,甲的速度是乙的2.5倍,4分钟两人首次相遇,此时乙还需要跑300米才跑完第一圈,求甲、乙二人的速度及环形场地的周长.(列方程组求解)【解析】设乙的速度为x米/分,
则甲的速度为2.5x米/分,环形场地的周长为y米,
由题意,得 解得:
∴甲的速度为:2.5×150=375米/分.
答:乙的速度为150米/分,甲的速度为375米/分,环形场地的周长为900米.2.为方便市民出行,减轻城市中心交通压力,长沙市正在修建贯穿星城南北、东西的地铁1,2号线.已知修建地铁1号线24千米和2号线22千米共需投资265亿元;若1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.
(1)求1号线,2号线每千米的平均造价分别是多少亿元?
(2)除1,2号线外,长沙市政府规划到2018年还需再建91.8千米的地铁线网.据预算,这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍,则还需投资多少亿元?【解析】(1)设1号线每千米的平均造价为x亿元,2号线每千
米的平均造价为y亿元,由题意得:
解得
答:1,2号线每千米的平均造价分别为6亿元、5.5亿元.
(2)91.8×6×1.2=660.96(亿元).
答:还需投资660.96亿元.3.某镇水库的可用水量为12 000万立方米,假设年降水量不变,能维持该镇16万人20年的用水量.实施城市化建设,新迁入4万人后,水库只够维持居民15年的用水量.
(1)问:年降水量为多少万立方米?每人年平均用水量多少立方米?
(2)政府号召节约用水,希望将水库的保用年限提高到25年,则该镇居民人均每年需节约多少立方米才能实现目标? 【解析】(1)设年降水量为x万立方米,每人年平均用水量为
y立方米,则: 解得:
答:年降水量为200万立方米,每人年平均用水量为50立方米.
(2)设该城镇居民年平均用水量为z立方米才能实现目标,则:
12 000+25×200=20×25z,解得:z=34.
∴50-34=16.
答:该城镇居民人均每年需要节约16立方米的水才能实现目标.4.用一根绳子绕一个圆柱形油桶.若环绕油
桶3周,则绳子还多4尺;若环绕油桶4周,则绳子又少了3尺.
这根绳子有多长?环绕油桶一周需要多少尺?
【解析】设这根绳子长为x尺,环绕油桶一周需y尺,由题意,
得 解得
答:这根绳子长为25尺,环绕油桶一周需7尺.5.为了进一步推进海南国际旅游岛建设,海口市自2012年4月1日起实施《海口市奖励旅行社开发客源市场暂行办法》,第八条规定:旅行社引进会议规模达到200人以上,入住本市A类旅游饭店,每次会议奖励2万元;入住本市B类旅游饭店,每次会议奖励1万元.某旅行社5月份引进符合奖励规定的会议18次,得到28万元奖金.求此旅行社引进符合奖励规定的入住A类和B类旅游饭店的会议各多少次.【解析】设入住A类旅游饭店的会议x次,入住B类旅游饭店的
会议y次.
根据题意,得 解得
答:此旅行社引进符合奖励规定的入住A类旅游饭店的会议
10次,入住B类旅游饭店的会议8次.【知识拓展】巧用“设而不求”化解问题
“设而不求”,顾名思义是除了设要求的未知数外,再多设另外一些相关的未知数作为辅助未知数,以便把已知和未知联系起来,易于建立方程(组),然后在解方程或方程组时,不必考虑辅助未知数的求解,只需直接考虑问题的解.请看:【例】某游泳选手携带一空水壶(可漂浮的)沿河逆流练习游泳,于A处不小心把水壶遗失,在他继续往前游了30分钟后才发现,于是立即返回追赶,结果在距离A处3千米的下游处追回.问河水的流速是多少?【解析】本题中除了所求的水流速度外,还有游泳者的速度、追赶水壶的时间.只有这些未知量都参与才能轻易地列出方程组.因此,除了设水流速度为x千米/时外,还需再设游泳者在静水中的速度为a千米/时,追赶水壶的时间为b小时,则依题意,有
①代入②,得(b+0.5)x=ab+bx-0.5a+0.5x, ③
所以0.5a=ab,
因为a≠0,所以b=0.5,从而由②得x=3.“设而不求”是解较高难度应用题的一种技巧,这种技巧源自方程组思想,当问题的已知条件给人一种感觉很少或“不足”时,“设而不求”将大显身手.
