华师大版初中数学七年级下册第8章一元一次不等式 章末复习课件(48张PPT)
文档属性
| 名称 | 华师大版初中数学七年级下册第8章一元一次不等式 章末复习课件(48张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 643.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-29 09:41:48 | ||
图片预览










文档简介
课件48张PPT。章末复习
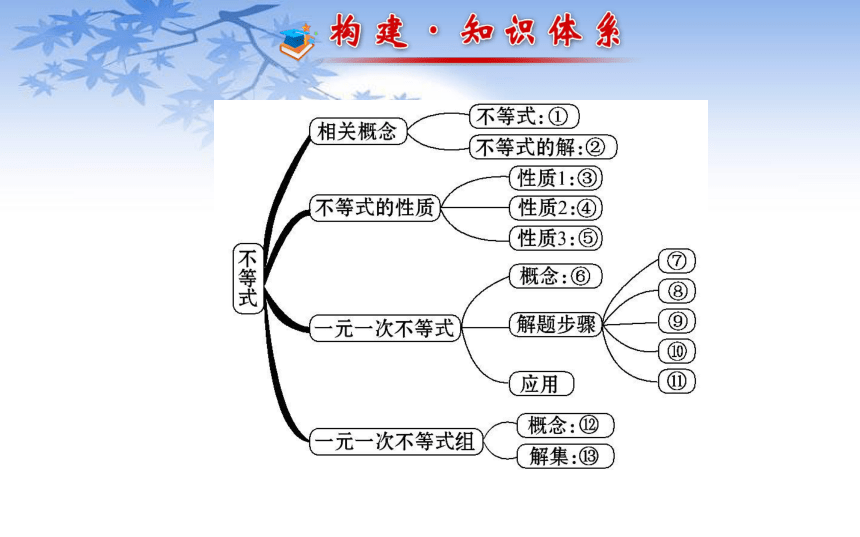
第 8 章请写出框图中数字处的内容:
①_______________________________________;
②_________________________;
③_________________________;
④_______________________________________;
⑤_______________________________________;
⑥___________________________________________________
____________________________________________;用不等号“>”或“<”表示不等关系的式子使不等式成立的未知数的值如果a>b,那么a±c>b±c如果a>b,并且c>0,那么ac>bc,如果a>b,并且c<0,那么ac<bc,含有一个未知数,并且含有未知数的式子是整式,未知数的次数都是1,这样的不等式叫做一元一次不等式⑦_______;⑧_______;⑨_____;⑩___________;
?_______________________;
?___________________________;
?_____________________________________.去分母去括号移项合并同类项两边都除以未知数的系数两个一元一次不等式合在一起不等式组中几个不等式的解集的公共部分考点 1 不等式的性质
【知识点睛】
应用不等式的性质应注意的事项
1.一变:不等式的两边都乘以或除以同一个负数,不等号的方向改变.2.两不变:
(1)不等式的两边都加上或减去同一个数或同一个整式,不等号的方向不变.
(2)不等式的两边都乘以或除以同一个正数,不等号的方向不变.【例1】若a>b>0,则下列不等式不一定成立的是( )
A. ac>bc B.a+c>b+c
C. D.ab>b2
【思路点拨】把各个选项与a>b对比,看发生了怎样的变化,然后判断变化的依据是否合理正确.【自主解答】选A.A.由a>b,得ac>bc,若c<0,不等号的方
向改变,故此选项错误;B.由a>b,得a+c>b+c,不等式两边加
上同一个数或同一个整式,不等号的方向不变,故此选项正
确;C.由a>b>0,得ab>0,在a>b的两边同除以ab,得
即 故C项正确;D.由a>b>0,得ab>b2,因为b>0,不等式
两边乘以同一个正数,不等号的方向不变,故此选项正确.【中考集训】
1.已知a>b,c≠0,则下列关系一定成立的是( )
A.ac>bc B.
C.c-a>c-b D.c+a>c+b【解析】选D.当c为负数时,根据不等式的性质3,不等号的方向应改变,所以选项A,B错误;根据不等式的性质,a>b两边先乘以-1,再加c,不等号的方向应改变,所以选项C错误;根据不等式的性质1,a>b两边加上c,得c+a>c+b,所以选项D正确.2.已知a<b,下列式子不成立的是( )
A.a+1<b+1 B.3a<3b
C. D.如果c<0,那么
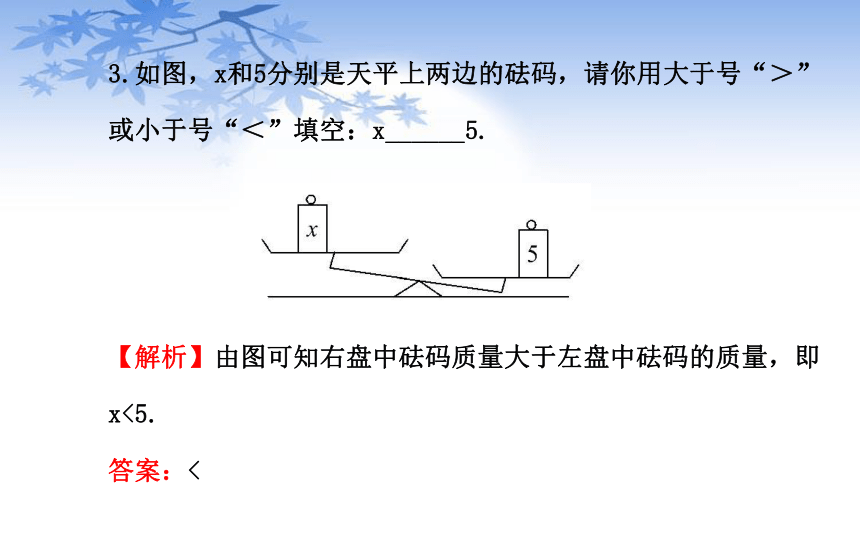
【解析】选D.如果c<0,根据不等式的性质3,不等号的方向应改变,所以选项D不成立.3.如图,x和5分别是天平上两边的砝码,请你用大于号“>”或小于号“<”填空:x______5.
【解析】由图可知右盘中砝码质量大于左盘中砝码的质量,即x<5.
答案:<考点 2 解一元一次不等式
【知识点睛】
1.解一元一次不等式的一般步骤:
(1)去分母:两边都乘以分母的最小公倍数.
(2)去括号:利用去括号法则或乘法分配律进行.
(3)移项:类似等式变形规则,把含有未知数的项移到不等式一边,常数项移到另一边.(4)合并同类项:按照合并同类项法则进行.
(5)两边都除以未知数的系数:依据是不等式的性质2或3.
以上五个步骤的先后顺序并非固定不变,要根据不等式的特点,确定恰当的步骤,灵活解不等式.2.注意事项:
(1)去分母:不等式两边都乘以分母的最小公倍数,注意不要漏乘,分子是多项式时要用括号括起来,若是乘以负数,不等号方向要改变.
(2)去括号:括号前是负号时,去掉括号后括号内的每项都变号,利用乘法分配律去括号时不要漏乘括号内的项.
(3)移项变号,不移不变号.(4)合并同类项:把不等式化为ax>b或ax(5)两边都除以未知数的系数:两边同乘(除)以负数时,防止出现忘记改变不等号方向的错误.【例2】解不等式:2(x+3)-4>0,并把解集在数轴上(如图)表示出来.
【思路点拨】去括号→移项→合并同类项→两边都除以未知数的系数→在数轴上表示.【自主解答】2(x+3)-4>0,
去括号,得2x+6-4>0,
移项,得2x>-6+4,
合并同类项,得2x>-2,
两边都除以2,得x>-1.
在数轴上表示为【中考集训】
1.不等式3x-6≥0的解集为( )
A.x>2 B.x≥2 C.x<2 D.x≤2
【解析】选B.移项得3x≥6,两边都除以3,得x≥2.2.已知不等式x-1≥0,此不等式的解集在数轴上表示为( )
【解析】选C.解不等式x-1≥0,得x≥1,有等号是实心圆点,大于向右.3.关于不等式-2x+a≥2的解集如图所示,
a的值是( )
A.0 B.2 C.-2 D.4
【解析】选A.移项,得-2x≥2-a,两边都除以-2,得x≤
观察数轴可知 =-1,解得a=0.4.关于x的方程mx-1=2x的解为正实数,则
m的取值范围是( )
A.m≥2 B.m≤2 C.m>2 D.m<2
【解析】选C.由mx-1=2x,(m-2)x=1,得:
因为方程mx-1=2x的解为正实数,所以 >0,解得m>2.5.不等式x-1≤10的解集是_____.
【解析】由x-1≤10,移项得x≤11.
答案:x≤116.解不等式4(x-1)+3≥3x,并把解集在数轴上表示出来.
【解析】去括号得4x-4+3≥3x,
移项得4x-3x≥4-3,
合并同类项得x≥1.
在数轴上表示不等式的解集为:【归纳整合】不等式(等式)性质、一元一次不等式(方程)的异同
1.等式的性质与不等式的性质异同:2.一元一次方程与一元一次不等式的异同:考点 3 解一元一次不等式组
【知识点睛】
一元一次不等式组常考知识点
1.解一元一次不等式组:对于不等式组的解集,需求出各个不等式的解集,再借助于数轴找出其公共部分.在确定不等式组的解集后, 还可结合数轴, 找出解集中某些特殊的解.2.求一元一次不等式组的特殊解:求一元一次不等式组的特殊解的一般步骤是:(1)求出一元一次不等式组的解集.(2)从解集里找出相应的整数解、非负整数解、自然数解等特殊解.
3.一元一次不等式组中待定字母的取值:先求含有字母系数不等式组的解集(用字母系数表示),再根据整数解的个数或已知解集,确定字母系数的值.【例3】解不等式组
【思路点拨】分别求解→确定解集.
【自主解答】
解不等式①得x<6.
解不等式②得x≥3.
所以原不等式组的解集为3≤x<6.【中考集训】
1.若关于x的不等式组的解表示在数轴上如图所示,则这个不等式组的解集是( )
A.x≤2 B.x>1
C.1≤x<2 D.1【解析】选D.解集在1和2之间,根据“空心圆圈”“实点”,可知解集不包括1,但包括2.2.不等式组 的解集在数轴上表示
为( )
【解析】选A.解不等式3x-1>2得x>1;解不等式4-2x≥0得x≤2,所以不等式组的解集是1A.x>2 B.x≤4
C.x<2或x≥4 D.2【解析】选D.解不等式5x-1>3(x+1),得x>2 ;
解不等式 得x≤4;
所以不等式组的解集为2是_______.
【解析】解不等式①得x> 解②得x≤1,所以不等式组的解集
是答案: 的所有的整数解.
【解析】解不等式①得3x-6≥x-4,2x≥2,x≥1,
解不等式②得2x+1>3x-3,-x>-4,x<4,
所以不等式组的解集是1≤x<4,
所以不等式组的所有的整数解是1,2,3.考点 4 一元一次不等式(组) 的应用
【知识点睛】
一元一次不等式(组) 应用的两个步骤
1.审题:找出关键词及不等关系.
2.列式求解:设出未知数, 依据不等关系列不等式(组)求解.【例4】暑期中,哥哥和弟弟二人分别编织28个中国结,已知弟弟单独编织一周(7天)不能完成,而哥哥单独编织不到一周就已完成.哥哥平均每天比弟弟多编2个.
求:(1)哥哥和弟弟平均每天各编多少个中国结?(答案取整数)
(2)若弟弟先工作2天,哥哥才开始工作,那么哥哥工作几天,两人所编中国结数量相同?【思路点拨】(1)设弟弟平均每天编x个中国结,根据弟弟单独工作一周(7天)不能完成,得7x<28;根据哥哥单独工作不到一周就已完成,得7(x+2)>28,列不等式组进行求解.
(2)设哥哥工作m天,两人所编中国结数量相同,结合(1)中求得的结果,列方程求解.【自主解答】(1)设弟弟平均每天编x个中国结,则哥哥平均每天编(x+2)个中国结.
依题意得:
解得:2因为x取正整数,
所以x=3.(2)设哥哥工作m天,两人所编中国结数量相同,
依题意得:3(m+2)=5m,
解得:m=3.
答:(1)哥哥平均每天编5个中国结,弟弟平均每天编3个中国结;(2)若弟弟先工作2天,哥哥才开始工作,那么哥哥工作3天,两人所编中国结数量相同.【中考集训】
1.某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到敬老院慰问老人.如果分给每位老人4盒牛奶,那么剩下28盒牛奶;如果分给每位老人5盒牛奶,那么最后一位老人分得的牛奶不足4盒,但至少1盒.则这个敬老院的老人最少有( )
A.29人 B.30人 C.31人 D.32人【解析】选B.设这个敬老院的老人有x人,依题意得:
解得29<x≤32,
因为x为整数,所以x最少为30.2.某商品的售价是528元,商家出售一件
这样的商品可获利润是进价的10%~20%,设进价为x元,则x
的取值范围是________.
【解析】由题意得到不等式:
解得440≤x≤480.
答案:440≤x≤4803.某企业向银行贷款1 000万元,一年后归还银行1 065.6万多元,则年利率高于_______%.
【解析】设年利率为x%,由题意可得不等式1 000(1+x%)> 1 065.6,解得x>6.56.
答案:6.564.某商场用36 000元购进甲、乙两种商品,销售完后共获利6 000元.其中甲种商品每件进价120元,售价138元;乙种商品每件进价100元,售价120元.
(1)该商场购进甲、乙两种商品各多少件?
(2)商场第二次以原进价购进甲、乙两种商品,购进乙种商品的件数不变,而购进甲种商品的件数是第一次的2倍,甲种商品按原售价出售,而乙种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于8 160元,乙种商品最低售价为每件多少元?【解析】(1)设商场购进甲种商品x件,购进乙种商品y件,根据题意得
解得
答:商场购进甲种商品200件,购进乙种商品120件.
(2)设乙种商品最低售价为每件z元,根据题意,得400×(138-120)+120×(z-100)≥8 160,解得z≥108.
答:乙种商品最低售价为每件108元.5.某中学计划从荣威公司购买A,B两种
型号的小黑板,经洽谈,购买一块A型小黑板比购买一块B型小
黑板多用20元,且购买5块A型小黑板和4块B型小黑板共需820
元,求:
(1)购买一块A型小黑板,一块B型小黑板各需多少元?
(2)根据这所中学的实际情况,需从荣威公司购买A,B两种小
黑板共60块,要求购买A,B两种型号小黑板的总费用不超过
5 240元,并且购买A型小黑板的数量应大于购买A,B两种型号
小黑板总数量的 请你通过计算,求出该中学从荣威公司购
买A,B两种型号的小黑板有哪几种方案?【解析】(1)设购买一块A型小黑板需要x元,则购买一块B型小黑板需要(x-20)元.
根据题意5x+4(x-20)=820,解得x=100.
答:购买一块A型小黑板需要100元,购买一块B型小黑板需要80元.(2)设购买A型小黑板m块,则购买B型小黑板(60-m)块.
根据题意
解得20<m≤22.
∵m为整数,∴m为21或22.
当m=21时,60-m=39;
当m=22时,60-m=38.
有两种购买方案:
方案一:购买A型小黑板21块,购买B型小黑板39块;
方案二:购买A型小黑板22块,购买B型小黑板38块.
第 8 章请写出框图中数字处的内容:
①_______________________________________;
②_________________________;
③_________________________;
④_______________________________________;
⑤_______________________________________;
⑥___________________________________________________
____________________________________________;用不等号“>”或“<”表示不等关系的式子使不等式成立的未知数的值如果a>b,那么a±c>b±c如果a>b,并且c>0,那么ac>bc,如果a>b,并且c<0,那么ac<bc,含有一个未知数,并且含有未知数的式子是整式,未知数的次数都是1,这样的不等式叫做一元一次不等式⑦_______;⑧_______;⑨_____;⑩___________;
?_______________________;
?___________________________;
?_____________________________________.去分母去括号移项合并同类项两边都除以未知数的系数两个一元一次不等式合在一起不等式组中几个不等式的解集的公共部分考点 1 不等式的性质
【知识点睛】
应用不等式的性质应注意的事项
1.一变:不等式的两边都乘以或除以同一个负数,不等号的方向改变.2.两不变:
(1)不等式的两边都加上或减去同一个数或同一个整式,不等号的方向不变.
(2)不等式的两边都乘以或除以同一个正数,不等号的方向不变.【例1】若a>b>0,则下列不等式不一定成立的是( )
A. ac>bc B.a+c>b+c
C. D.ab>b2
【思路点拨】把各个选项与a>b对比,看发生了怎样的变化,然后判断变化的依据是否合理正确.【自主解答】选A.A.由a>b,得ac>bc,若c<0,不等号的方
向改变,故此选项错误;B.由a>b,得a+c>b+c,不等式两边加
上同一个数或同一个整式,不等号的方向不变,故此选项正
确;C.由a>b>0,得ab>0,在a>b的两边同除以ab,得
即 故C项正确;D.由a>b>0,得ab>b2,因为b>0,不等式
两边乘以同一个正数,不等号的方向不变,故此选项正确.【中考集训】
1.已知a>b,c≠0,则下列关系一定成立的是( )
A.ac>bc B.
C.c-a>c-b D.c+a>c+b【解析】选D.当c为负数时,根据不等式的性质3,不等号的方向应改变,所以选项A,B错误;根据不等式的性质,a>b两边先乘以-1,再加c,不等号的方向应改变,所以选项C错误;根据不等式的性质1,a>b两边加上c,得c+a>c+b,所以选项D正确.2.已知a<b,下列式子不成立的是( )
A.a+1<b+1 B.3a<3b
C. D.如果c<0,那么
【解析】选D.如果c<0,根据不等式的性质3,不等号的方向应改变,所以选项D不成立.3.如图,x和5分别是天平上两边的砝码,请你用大于号“>”或小于号“<”填空:x______5.
【解析】由图可知右盘中砝码质量大于左盘中砝码的质量,即x<5.
答案:<考点 2 解一元一次不等式
【知识点睛】
1.解一元一次不等式的一般步骤:
(1)去分母:两边都乘以分母的最小公倍数.
(2)去括号:利用去括号法则或乘法分配律进行.
(3)移项:类似等式变形规则,把含有未知数的项移到不等式一边,常数项移到另一边.(4)合并同类项:按照合并同类项法则进行.
(5)两边都除以未知数的系数:依据是不等式的性质2或3.
以上五个步骤的先后顺序并非固定不变,要根据不等式的特点,确定恰当的步骤,灵活解不等式.2.注意事项:
(1)去分母:不等式两边都乘以分母的最小公倍数,注意不要漏乘,分子是多项式时要用括号括起来,若是乘以负数,不等号方向要改变.
(2)去括号:括号前是负号时,去掉括号后括号内的每项都变号,利用乘法分配律去括号时不要漏乘括号内的项.
(3)移项变号,不移不变号.(4)合并同类项:把不等式化为ax>b或ax
【思路点拨】去括号→移项→合并同类项→两边都除以未知数的系数→在数轴上表示.【自主解答】2(x+3)-4>0,
去括号,得2x+6-4>0,
移项,得2x>-6+4,
合并同类项,得2x>-2,
两边都除以2,得x>-1.
在数轴上表示为【中考集训】
1.不等式3x-6≥0的解集为( )
A.x>2 B.x≥2 C.x<2 D.x≤2
【解析】选B.移项得3x≥6,两边都除以3,得x≥2.2.已知不等式x-1≥0,此不等式的解集在数轴上表示为( )
【解析】选C.解不等式x-1≥0,得x≥1,有等号是实心圆点,大于向右.3.关于不等式-2x+a≥2的解集如图所示,
a的值是( )
A.0 B.2 C.-2 D.4
【解析】选A.移项,得-2x≥2-a,两边都除以-2,得x≤
观察数轴可知 =-1,解得a=0.4.关于x的方程mx-1=2x的解为正实数,则
m的取值范围是( )
A.m≥2 B.m≤2 C.m>2 D.m<2
【解析】选C.由mx-1=2x,(m-2)x=1,得:
因为方程mx-1=2x的解为正实数,所以 >0,解得m>2.5.不等式x-1≤10的解集是_____.
【解析】由x-1≤10,移项得x≤11.
答案:x≤116.解不等式4(x-1)+3≥3x,并把解集在数轴上表示出来.
【解析】去括号得4x-4+3≥3x,
移项得4x-3x≥4-3,
合并同类项得x≥1.
在数轴上表示不等式的解集为:【归纳整合】不等式(等式)性质、一元一次不等式(方程)的异同
1.等式的性质与不等式的性质异同:2.一元一次方程与一元一次不等式的异同:考点 3 解一元一次不等式组
【知识点睛】
一元一次不等式组常考知识点
1.解一元一次不等式组:对于不等式组的解集,需求出各个不等式的解集,再借助于数轴找出其公共部分.在确定不等式组的解集后, 还可结合数轴, 找出解集中某些特殊的解.2.求一元一次不等式组的特殊解:求一元一次不等式组的特殊解的一般步骤是:(1)求出一元一次不等式组的解集.(2)从解集里找出相应的整数解、非负整数解、自然数解等特殊解.
3.一元一次不等式组中待定字母的取值:先求含有字母系数不等式组的解集(用字母系数表示),再根据整数解的个数或已知解集,确定字母系数的值.【例3】解不等式组
【思路点拨】分别求解→确定解集.
【自主解答】
解不等式①得x<6.
解不等式②得x≥3.
所以原不等式组的解集为3≤x<6.【中考集训】
1.若关于x的不等式组的解表示在数轴上如图所示,则这个不等式组的解集是( )
A.x≤2 B.x>1
C.1≤x<2 D.1
为( )
【解析】选A.解不等式3x-1>2得x>1;解不等式4-2x≥0得x≤2,所以不等式组的解集是1
C.x<2或x≥4 D.2
解不等式 得x≤4;
所以不等式组的解集为2
【解析】解不等式①得x> 解②得x≤1,所以不等式组的解集
是
【解析】解不等式①得3x-6≥x-4,2x≥2,x≥1,
解不等式②得2x+1>3x-3,-x>-4,x<4,
所以不等式组的解集是1≤x<4,
所以不等式组的所有的整数解是1,2,3.考点 4 一元一次不等式(组) 的应用
【知识点睛】
一元一次不等式(组) 应用的两个步骤
1.审题:找出关键词及不等关系.
2.列式求解:设出未知数, 依据不等关系列不等式(组)求解.【例4】暑期中,哥哥和弟弟二人分别编织28个中国结,已知弟弟单独编织一周(7天)不能完成,而哥哥单独编织不到一周就已完成.哥哥平均每天比弟弟多编2个.
求:(1)哥哥和弟弟平均每天各编多少个中国结?(答案取整数)
(2)若弟弟先工作2天,哥哥才开始工作,那么哥哥工作几天,两人所编中国结数量相同?【思路点拨】(1)设弟弟平均每天编x个中国结,根据弟弟单独工作一周(7天)不能完成,得7x<28;根据哥哥单独工作不到一周就已完成,得7(x+2)>28,列不等式组进行求解.
(2)设哥哥工作m天,两人所编中国结数量相同,结合(1)中求得的结果,列方程求解.【自主解答】(1)设弟弟平均每天编x个中国结,则哥哥平均每天编(x+2)个中国结.
依题意得:
解得:2
所以x=3.(2)设哥哥工作m天,两人所编中国结数量相同,
依题意得:3(m+2)=5m,
解得:m=3.
答:(1)哥哥平均每天编5个中国结,弟弟平均每天编3个中国结;(2)若弟弟先工作2天,哥哥才开始工作,那么哥哥工作3天,两人所编中国结数量相同.【中考集训】
1.某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到敬老院慰问老人.如果分给每位老人4盒牛奶,那么剩下28盒牛奶;如果分给每位老人5盒牛奶,那么最后一位老人分得的牛奶不足4盒,但至少1盒.则这个敬老院的老人最少有( )
A.29人 B.30人 C.31人 D.32人【解析】选B.设这个敬老院的老人有x人,依题意得:
解得29<x≤32,
因为x为整数,所以x最少为30.2.某商品的售价是528元,商家出售一件
这样的商品可获利润是进价的10%~20%,设进价为x元,则x
的取值范围是________.
【解析】由题意得到不等式:
解得440≤x≤480.
答案:440≤x≤4803.某企业向银行贷款1 000万元,一年后归还银行1 065.6万多元,则年利率高于_______%.
【解析】设年利率为x%,由题意可得不等式1 000(1+x%)> 1 065.6,解得x>6.56.
答案:6.564.某商场用36 000元购进甲、乙两种商品,销售完后共获利6 000元.其中甲种商品每件进价120元,售价138元;乙种商品每件进价100元,售价120元.
(1)该商场购进甲、乙两种商品各多少件?
(2)商场第二次以原进价购进甲、乙两种商品,购进乙种商品的件数不变,而购进甲种商品的件数是第一次的2倍,甲种商品按原售价出售,而乙种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于8 160元,乙种商品最低售价为每件多少元?【解析】(1)设商场购进甲种商品x件,购进乙种商品y件,根据题意得
解得
答:商场购进甲种商品200件,购进乙种商品120件.
(2)设乙种商品最低售价为每件z元,根据题意,得400×(138-120)+120×(z-100)≥8 160,解得z≥108.
答:乙种商品最低售价为每件108元.5.某中学计划从荣威公司购买A,B两种
型号的小黑板,经洽谈,购买一块A型小黑板比购买一块B型小
黑板多用20元,且购买5块A型小黑板和4块B型小黑板共需820
元,求:
(1)购买一块A型小黑板,一块B型小黑板各需多少元?
(2)根据这所中学的实际情况,需从荣威公司购买A,B两种小
黑板共60块,要求购买A,B两种型号小黑板的总费用不超过
5 240元,并且购买A型小黑板的数量应大于购买A,B两种型号
小黑板总数量的 请你通过计算,求出该中学从荣威公司购
买A,B两种型号的小黑板有哪几种方案?【解析】(1)设购买一块A型小黑板需要x元,则购买一块B型小黑板需要(x-20)元.
根据题意5x+4(x-20)=820,解得x=100.
答:购买一块A型小黑板需要100元,购买一块B型小黑板需要80元.(2)设购买A型小黑板m块,则购买B型小黑板(60-m)块.
根据题意
解得20<m≤22.
∵m为整数,∴m为21或22.
当m=21时,60-m=39;
当m=22时,60-m=38.
有两种购买方案:
方案一:购买A型小黑板21块,购买B型小黑板39块;
方案二:购买A型小黑板22块,购买B型小黑板38块.
