高中数学人教A版选修4-4第一讲极坐标系及简单曲线的极坐标方程(共32张PPT)
文档属性
| 名称 | 高中数学人教A版选修4-4第一讲极坐标系及简单曲线的极坐标方程(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 10:58:23 | ||
图片预览






文档简介
(共32张PPT)
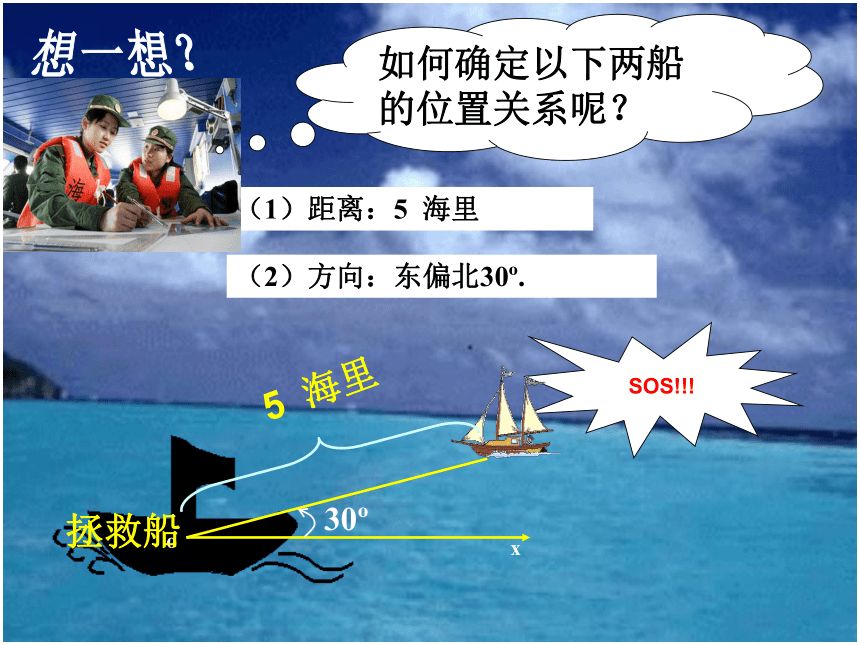
5 海里
(1)距离:5 海里
(2)方向:东偏北30?.
o
x
拯救船
30?
SOS!!!
如何确定以下两船的位置关系呢?
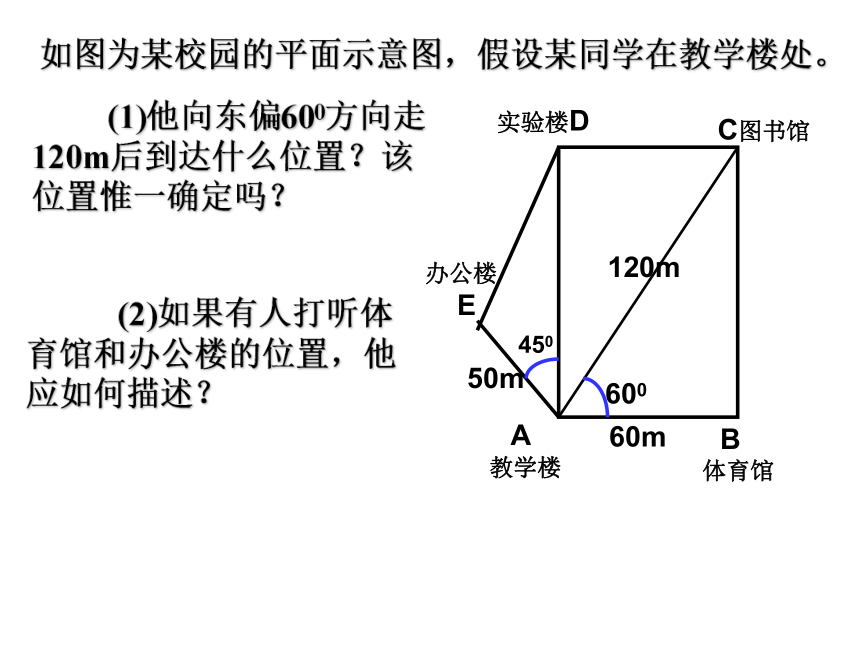
如图为某校园的平面示意图,假设某同学在教学楼处。
(2)如果有人打听体育馆和办公楼的位置,他应如何描述?
(1)他向东偏600方向走120m后到达什么位置?该位置惟一确定吗?
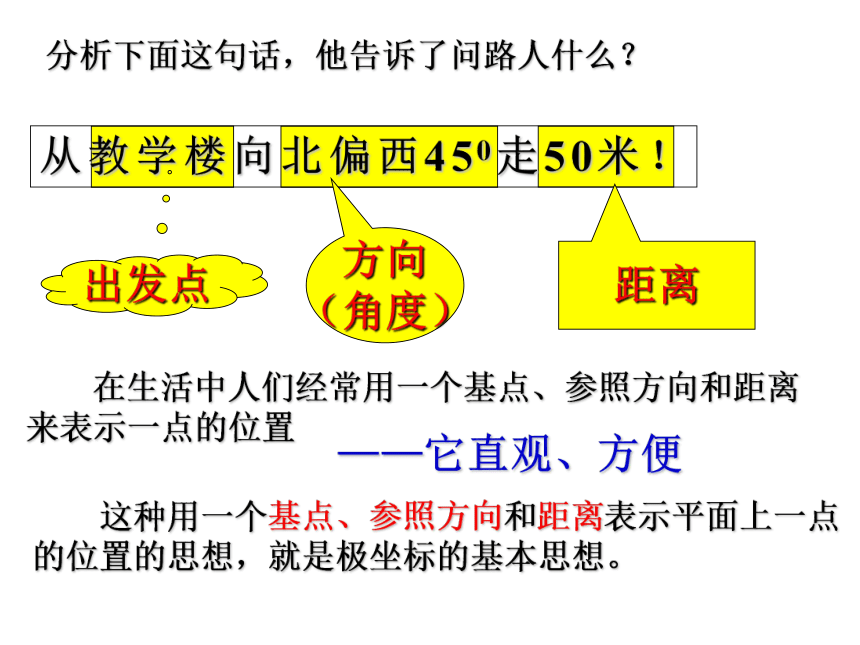
从教学楼向北偏西450走50米!
出发点
方向
(角度)
距离
在生活中人们经常用一个基点、参照方向和距离来表示一点的位置
这种用一个基点、参照方向和距离表示平面上一点的位置的思想,就是极坐标的基本思想。
——它直观、方便
分析下面这句话,他告诉了问路人什么?
O
在平面内取一个定点O,叫做极点。
自极点引一条射线OX,叫做极轴。
再选定一个长度单位和
角度单位(一般用弧度制)及
它的正方向(通常取逆时针方向)。
这样就建立了一个极坐标系。
一、极坐标系
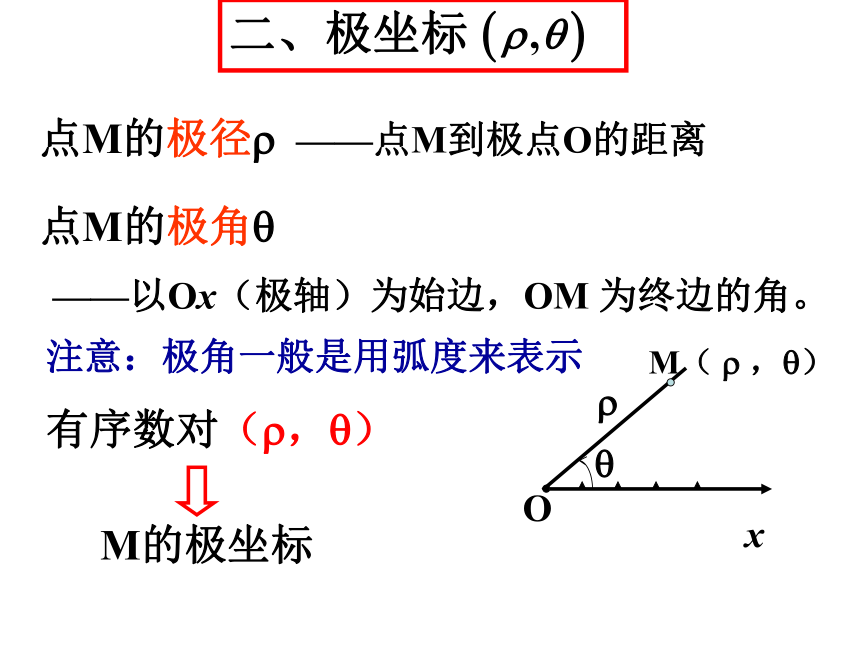
二、极坐标
M( ? ,?)
?
?
点M的极径?
注意:极角一般是用弧度来表示
点M的极角?
有序数对(?,?)
——点M到极点O的距离
——以Ox(极轴)为始边,OM 为终边的角。
M的极坐标
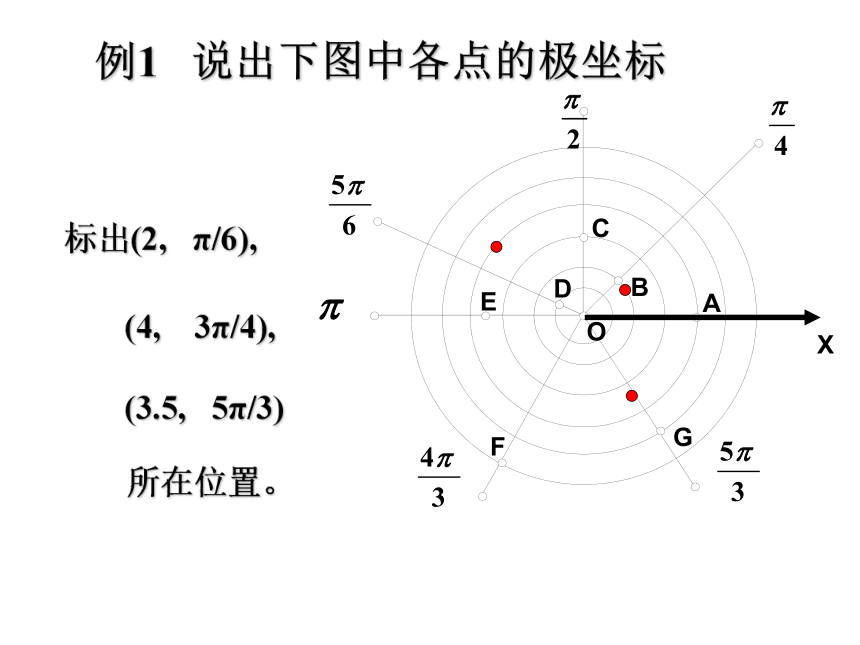
例1 说出下图中各点的极坐标
标出(2, π/6),
(4, 3π/4),
(3.5, 5π/3)
所在位置。
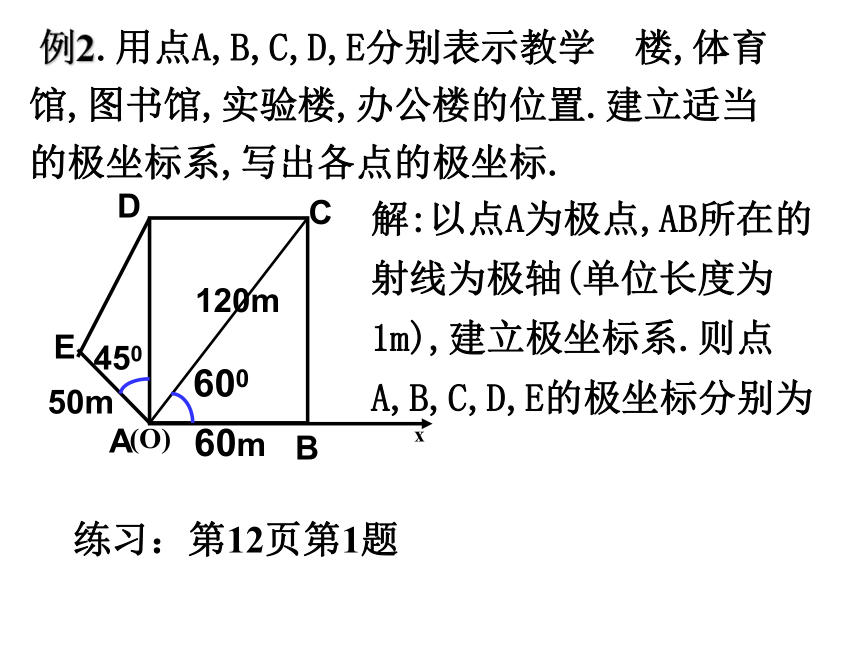
例2.用点A,B,C,D,E分别表示教学 楼,体育馆,图书馆,实验楼,办公楼的位置.建立适当的极坐标系,写出各点的极坐标.
解:以点A为极点,AB所在的
射线为极轴(单位长度为1m),建立极坐标系.则点A,B,C,D,E的极坐标分别为
练习:第12页第1题
建立了极坐标后,给定ρ、?,就可以在平面内惟一确定点M,
反过来,给定平面内任意一点,也可以找到它的极坐标(?,?)。
点与它的极坐标是否一一对应?
1.这些极坐标之间有何异同?
极径相同,极角不同。
2. 这些极角有何关系?
极角的始边相同,终边也相同,
即:它们是终边相同的角。
3. 这些极坐标所表示的点有什么关系?
它们表示同一个点。
在同一极坐标系中, 有如下极坐标:
点的极坐标的统一表达式:
平面内点的极坐标有无数种表示。
极点的坐标表示为(0,θ), θ为任意角
横坐标、纵坐标
角度和距离
点与坐标
一一对应
点与极坐标
不一一对应
极点,极轴,长度单位;角度单位
和正方向
原点,x,y轴长度单位和正方向
极坐标与直角坐标的区别
要素
极坐标系
平面直角坐系
定位方式
点与坐标
三、极坐标与直角坐标的互化
设点M的直角坐标是 (x, y),
极坐标是 (ρ,θ)
通常情况下,将点的直角坐标, 化为极坐标时,取
例1. 将点M的极坐标 化成直角坐标.
练习:第12页第4题
例2. 将点M的直角坐标 化成极坐标.
练习:第12页第5,3题
例3 已知两点 ,
求两点间的距离.
o
x
A
B
互化公式的三个前提条件:
1. 极点与直角坐标系的原点重合;
2. 极轴与直角坐标系的x轴的正半轴重合;
3. 两种坐标系的单位长度相同.
直角坐标
(x, y)
极坐标
(ρ,θ)
注意:点的象限位置
决定极角的象限位置
3、极坐标与直角坐标的互化公式
1、极坐标系的四要素
2、点与其极坐标一一对应的条件
极点;极轴;长度单位;角度单位及它的正方向。
1.已知下列点的极坐标,求它们的直角坐标。
2. 已知点的直角坐标, 求它们的极坐标.
x
如图,半径为a的圆的圆心坐标
为(a,0)(a>0), 你能用一个等式表示圆上
任意一点的极坐标(?,?)满足的条件?
O
M
θ
ρ
一、圆的极坐标方程
例1已知圆O的半径为r,建立怎样的坐标系,
可以使圆的极坐标方程更简单?
?=2
?=2acos ?
?=2asin ?
1.求下列圆的极坐标方程
(1)中心在极点,半径为2;
(2)中心在C(a,0),半径为a ;
(3)中心在( a , ),半径为a ;
2.极坐标方程分别是ρ=cosθ和
ρ=sinθ的两个圆的圆心距是多少?
3.求以直角坐标系中的点(1,1)为圆心,1为半径的圆的极坐标方程
ρ2-2 ρ cosθ-2ρ sinθ+1=0
在平面直角坐标系中,
1、过点(3,0)且与x轴垂直的直线方程为 ;过点(3,3)且与x轴垂直的直线方程为
x=3
x=3
2、过点(a,b)且垂直于x轴的直线方程为_______
x=a
特点:所有点的横坐标都是一样,纵坐标可以取任意值。
分析:
极径可以取任意的非负数。故所求
直线的极坐标方程为
二、直线的极坐标方程
对比:求过极点,倾角为 的射线的极坐标方程。
和前面的直角坐标系里直线方程的表示形式比较起来,极坐标系里的直线表示起来很不方便,要用两条射线组合而成。原因在哪?
为了弥补这个不足,可以考虑允许极径可以取全体实数。则上面的直线的极坐标方程可以表示为
或
例题2 求过点A(a,0)(a>0),且垂直于极轴的直线L的极坐标方程。
为直线L上除点A外的任意一点,连接OM
即
思考有没有更好的解法?
三、曲线的极坐标方程和直角坐标的互化
例1
例2
例3
例4
练习:第15页第3,4题
1
3
1
3
5 海里
(1)距离:5 海里
(2)方向:东偏北30?.
o
x
拯救船
30?
SOS!!!
如何确定以下两船的位置关系呢?
如图为某校园的平面示意图,假设某同学在教学楼处。
(2)如果有人打听体育馆和办公楼的位置,他应如何描述?
(1)他向东偏600方向走120m后到达什么位置?该位置惟一确定吗?
从教学楼向北偏西450走50米!
出发点
方向
(角度)
距离
在生活中人们经常用一个基点、参照方向和距离来表示一点的位置
这种用一个基点、参照方向和距离表示平面上一点的位置的思想,就是极坐标的基本思想。
——它直观、方便
分析下面这句话,他告诉了问路人什么?
O
在平面内取一个定点O,叫做极点。
自极点引一条射线OX,叫做极轴。
再选定一个长度单位和
角度单位(一般用弧度制)及
它的正方向(通常取逆时针方向)。
这样就建立了一个极坐标系。
一、极坐标系
二、极坐标
M( ? ,?)
?
?
点M的极径?
注意:极角一般是用弧度来表示
点M的极角?
有序数对(?,?)
——点M到极点O的距离
——以Ox(极轴)为始边,OM 为终边的角。
M的极坐标
例1 说出下图中各点的极坐标
标出(2, π/6),
(4, 3π/4),
(3.5, 5π/3)
所在位置。
例2.用点A,B,C,D,E分别表示教学 楼,体育馆,图书馆,实验楼,办公楼的位置.建立适当的极坐标系,写出各点的极坐标.
解:以点A为极点,AB所在的
射线为极轴(单位长度为1m),建立极坐标系.则点A,B,C,D,E的极坐标分别为
练习:第12页第1题
建立了极坐标后,给定ρ、?,就可以在平面内惟一确定点M,
反过来,给定平面内任意一点,也可以找到它的极坐标(?,?)。
点与它的极坐标是否一一对应?
1.这些极坐标之间有何异同?
极径相同,极角不同。
2. 这些极角有何关系?
极角的始边相同,终边也相同,
即:它们是终边相同的角。
3. 这些极坐标所表示的点有什么关系?
它们表示同一个点。
在同一极坐标系中, 有如下极坐标:
点的极坐标的统一表达式:
平面内点的极坐标有无数种表示。
极点的坐标表示为(0,θ), θ为任意角
横坐标、纵坐标
角度和距离
点与坐标
一一对应
点与极坐标
不一一对应
极点,极轴,长度单位;角度单位
和正方向
原点,x,y轴长度单位和正方向
极坐标与直角坐标的区别
要素
极坐标系
平面直角坐系
定位方式
点与坐标
三、极坐标与直角坐标的互化
设点M的直角坐标是 (x, y),
极坐标是 (ρ,θ)
通常情况下,将点的直角坐标, 化为极坐标时,取
例1. 将点M的极坐标 化成直角坐标.
练习:第12页第4题
例2. 将点M的直角坐标 化成极坐标.
练习:第12页第5,3题
例3 已知两点 ,
求两点间的距离.
o
x
A
B
互化公式的三个前提条件:
1. 极点与直角坐标系的原点重合;
2. 极轴与直角坐标系的x轴的正半轴重合;
3. 两种坐标系的单位长度相同.
直角坐标
(x, y)
极坐标
(ρ,θ)
注意:点的象限位置
决定极角的象限位置
3、极坐标与直角坐标的互化公式
1、极坐标系的四要素
2、点与其极坐标一一对应的条件
极点;极轴;长度单位;角度单位及它的正方向。
1.已知下列点的极坐标,求它们的直角坐标。
2. 已知点的直角坐标, 求它们的极坐标.
x
如图,半径为a的圆的圆心坐标
为(a,0)(a>0), 你能用一个等式表示圆上
任意一点的极坐标(?,?)满足的条件?
O
M
θ
ρ
一、圆的极坐标方程
例1已知圆O的半径为r,建立怎样的坐标系,
可以使圆的极坐标方程更简单?
?=2
?=2acos ?
?=2asin ?
1.求下列圆的极坐标方程
(1)中心在极点,半径为2;
(2)中心在C(a,0),半径为a ;
(3)中心在( a , ),半径为a ;
2.极坐标方程分别是ρ=cosθ和
ρ=sinθ的两个圆的圆心距是多少?
3.求以直角坐标系中的点(1,1)为圆心,1为半径的圆的极坐标方程
ρ2-2 ρ cosθ-2ρ sinθ+1=0
在平面直角坐标系中,
1、过点(3,0)且与x轴垂直的直线方程为 ;过点(3,3)且与x轴垂直的直线方程为
x=3
x=3
2、过点(a,b)且垂直于x轴的直线方程为_______
x=a
特点:所有点的横坐标都是一样,纵坐标可以取任意值。
分析:
极径可以取任意的非负数。故所求
直线的极坐标方程为
二、直线的极坐标方程
对比:求过极点,倾角为 的射线的极坐标方程。
和前面的直角坐标系里直线方程的表示形式比较起来,极坐标系里的直线表示起来很不方便,要用两条射线组合而成。原因在哪?
为了弥补这个不足,可以考虑允许极径可以取全体实数。则上面的直线的极坐标方程可以表示为
或
例题2 求过点A(a,0)(a>0),且垂直于极轴的直线L的极坐标方程。
为直线L上除点A外的任意一点,连接OM
即
思考有没有更好的解法?
三、曲线的极坐标方程和直角坐标的互化
例1
例2
例3
例4
练习:第15页第3,4题
1
3
1
3
