人教高中数学必修五1.2正弦定理余弦定理应用举例 课件(24张ppt)
文档属性
| 名称 | 人教高中数学必修五1.2正弦定理余弦定理应用举例 课件(24张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 21:24:44 | ||
图片预览





文档简介
(共24张PPT)
6.4.3 正弦定理,余弦定理应用举例
复习
正弦定理:
余弦定理:
三角形边与角的关系:
2、 大角对大边,小角对小边 。
余弦定理的应用条件:
(1)已知三边,求三个角。
(2)已知两边和它们的夹角,求第三边和其它两角。
(3)已知两边及对角,求第三边和其它两角。
正弦定理的应用条件:
(1)两角和一边,先求第三角,再用正弦定理。
(2)已知两边及对角,求第三边和其它两角。
实际应用问题中有关的名称、术语
1.仰角、俯角、视角。
(1)当视线在水平线上方时,视线与水平线所成角叫仰角。
(2)当视线在水平线下方时,视线与水平线所成角叫俯角。
(3)由一点出发的两条视线所夹的角叫视角。(一般这两条视线过被观察物的两端点)
水平线
视线
视线
仰角
俯角
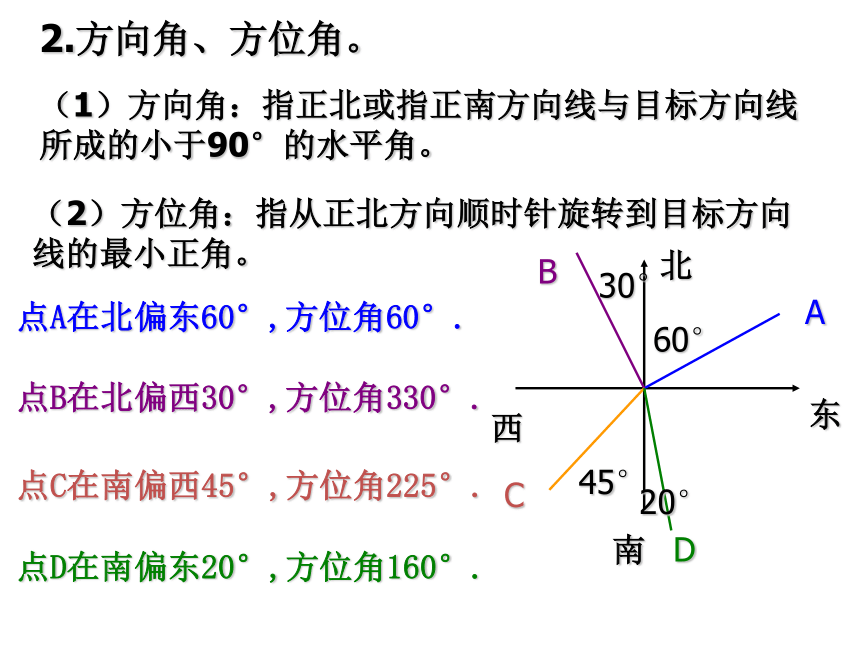
2.方向角、方位角。
(1)方向角:指正北或指正南方向线与目标方向线所成的小于90°的水平角。
(2)方位角:指从正北方向顺时针旋转到目标方向线的最小正角。
点A在北偏东60°,方位角60°.
点B在北偏西30°,方位角330°.
点C在南偏西45°,方位角225°.
点D在南偏东20°,方位角160°.
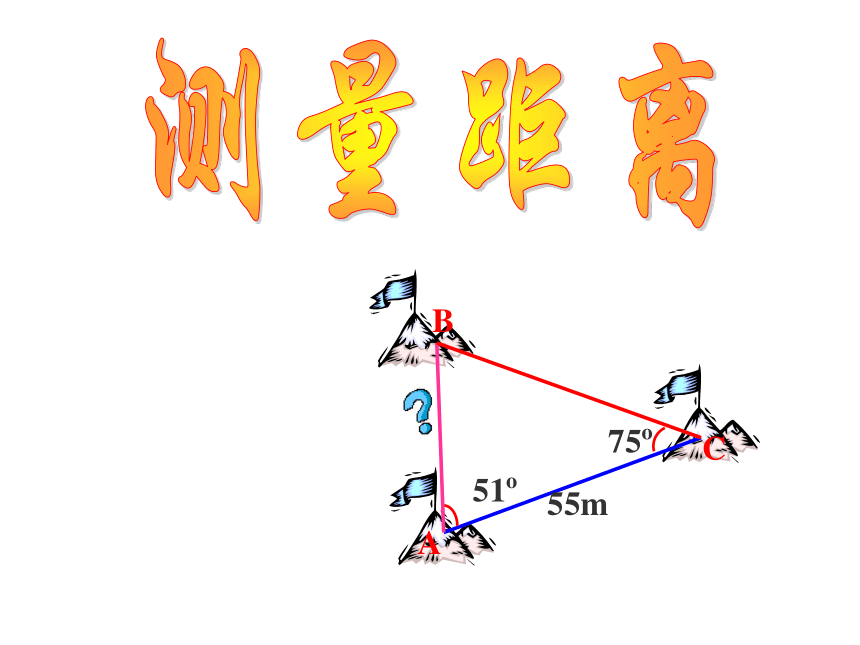
A
C
B
51o
55m
75o
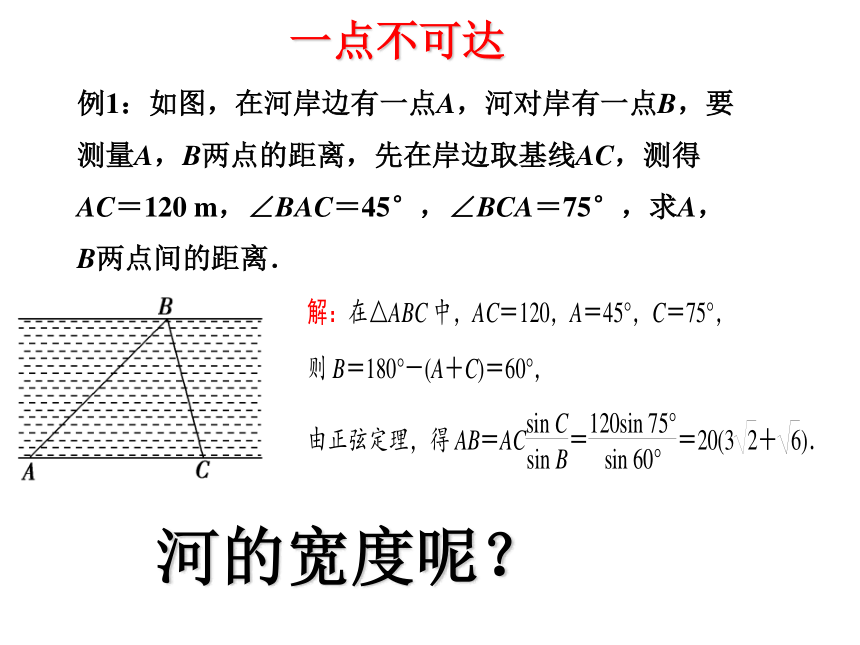
例1:如图,在河岸边有一点A,河对岸有一点B,要测量A,B两点的距离,先在岸边取基线AC,测得AC=120 m,∠BAC=45°,∠BCA=75°,求A,B两点间的距离.
河的宽度呢?
一点不可达
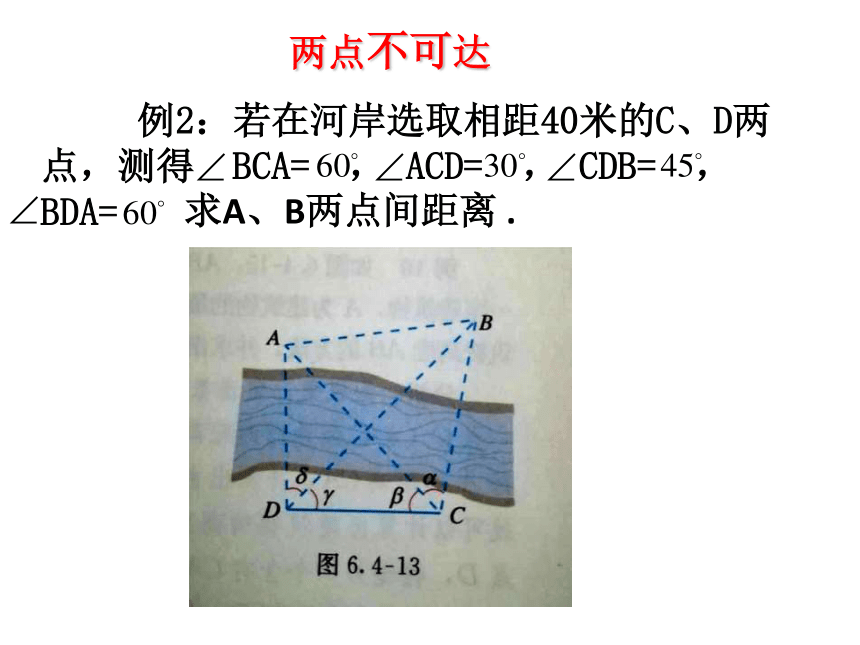
两点不可达
并且在C、D两点分别测得∠BCA=60°, ∠ACD=30°, ∠CDB=45°, ∠BDA=60°.
在⊿ADC和⊿BDC中,应用正弦定理得
解:CD=40m,
这样在三角形ABC中,∠BCA=60°,
由余弦定理得:
答:A,B两点间的距离为 米.
解:
并且在C、D两点分别测得∠BCA=60°, ∠ACD=30°, ∠CDB=45°, ∠BDA=60°.
在⊿ADC和⊿BDC中,应用正弦定理得
CD=40m,
这样在三角形ABD中,∠BDA=60°,
由余弦定理得:
答:A,B两点间的距离为 米.
底部不可达
解:在三角形ABC中, ∠ABC= 90° -α=30°, ∠BAC=α-β=15°, ∠ACD=45°.根据正弦定理,
【例5】
缉私艇在A点发现在北偏东45°方向,距离12 n mile的海面上有一走私船位于C点正以10 n mile/h的速度沿东偏南15°方向逃窜.缉私艇的速度为14 n mile/h.若要在最短的时间内追上该走私船,缉私艇应沿北偏东45°+α的方向去追.求追及所需的时间和角α的正弦值.
例6
练习
6.4.3 正弦定理,余弦定理应用举例
复习
正弦定理:
余弦定理:
三角形边与角的关系:
2、 大角对大边,小角对小边 。
余弦定理的应用条件:
(1)已知三边,求三个角。
(2)已知两边和它们的夹角,求第三边和其它两角。
(3)已知两边及对角,求第三边和其它两角。
正弦定理的应用条件:
(1)两角和一边,先求第三角,再用正弦定理。
(2)已知两边及对角,求第三边和其它两角。
实际应用问题中有关的名称、术语
1.仰角、俯角、视角。
(1)当视线在水平线上方时,视线与水平线所成角叫仰角。
(2)当视线在水平线下方时,视线与水平线所成角叫俯角。
(3)由一点出发的两条视线所夹的角叫视角。(一般这两条视线过被观察物的两端点)
水平线
视线
视线
仰角
俯角
2.方向角、方位角。
(1)方向角:指正北或指正南方向线与目标方向线所成的小于90°的水平角。
(2)方位角:指从正北方向顺时针旋转到目标方向线的最小正角。
点A在北偏东60°,方位角60°.
点B在北偏西30°,方位角330°.
点C在南偏西45°,方位角225°.
点D在南偏东20°,方位角160°.
A
C
B
51o
55m
75o
例1:如图,在河岸边有一点A,河对岸有一点B,要测量A,B两点的距离,先在岸边取基线AC,测得AC=120 m,∠BAC=45°,∠BCA=75°,求A,B两点间的距离.
河的宽度呢?
一点不可达
两点不可达
并且在C、D两点分别测得∠BCA=60°, ∠ACD=30°, ∠CDB=45°, ∠BDA=60°.
在⊿ADC和⊿BDC中,应用正弦定理得
解:CD=40m,
这样在三角形ABC中,∠BCA=60°,
由余弦定理得:
答:A,B两点间的距离为 米.
解:
并且在C、D两点分别测得∠BCA=60°, ∠ACD=30°, ∠CDB=45°, ∠BDA=60°.
在⊿ADC和⊿BDC中,应用正弦定理得
CD=40m,
这样在三角形ABD中,∠BDA=60°,
由余弦定理得:
答:A,B两点间的距离为 米.
底部不可达
解:在三角形ABC中, ∠ABC= 90° -α=30°, ∠BAC=α-β=15°, ∠ACD=45°.根据正弦定理,
【例5】
缉私艇在A点发现在北偏东45°方向,距离12 n mile的海面上有一走私船位于C点正以10 n mile/h的速度沿东偏南15°方向逃窜.缉私艇的速度为14 n mile/h.若要在最短的时间内追上该走私船,缉私艇应沿北偏东45°+α的方向去追.求追及所需的时间和角α的正弦值.
例6
练习
