新人教版物理必修二6.2--太阳与行星间的引力(30张PPT)
文档属性
| 名称 | 新人教版物理必修二6.2--太阳与行星间的引力(30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 787.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-03-29 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
太阳与行星间的引力
注意:k值与中心天体有关,而与环绕天体无关。
回顾:
开普勒行星运动定律
即:
思考:是什么原因使行星绕太阳运动呢?
猜想的逻辑顺序:
曲线运动—变速运动—加速度—合外力—引力
行星的运动是受到了来自太阳的类似于磁力的作用 ,与距离成反比。
行星的运动是太阳吸引的缘故,并且力的大小与到太阳距离的平方成反比。
在行星的周围有旋转的物质(以太)作用在行星上,使得行星绕太阳运动。
一切物体都有合并的趋势。
科学足迹
科学足迹
牛顿 (1643—1727)
英国著名的物理学家
当年牛顿在前人研究的基础上,也经过类似同学这样的思考,并凭借其超凡的数学能力和坚定的信念,深入研究,最终发现了万有引力定律。
牛顿在1676年给友人的信中写道:
如果说我看的比别人更远,那是因为我站在巨人的肩膀上。
猜想:引力大小跟什么有关?
追寻牛顿的足迹
讨论验证思路:
由运动情况----加速度----受力情况
一、太阳对行星的引力
1、设行星的质量为m,速度为v,行星到太阳的距离为r,则行星绕太阳做匀速圆周运动的向心力为多少?
代入
由
2、天文观测难以直接得到行星的速度v,但可以得到行星的公转周期T
得到:
3、根据开普勒第三定律:
即
得
代入
4、太阳对行星的引力 :
即:
这表明:太阳对不同行星的引力,与行星的质量成正比,与行星和太阳间的距离的二次方成反比。
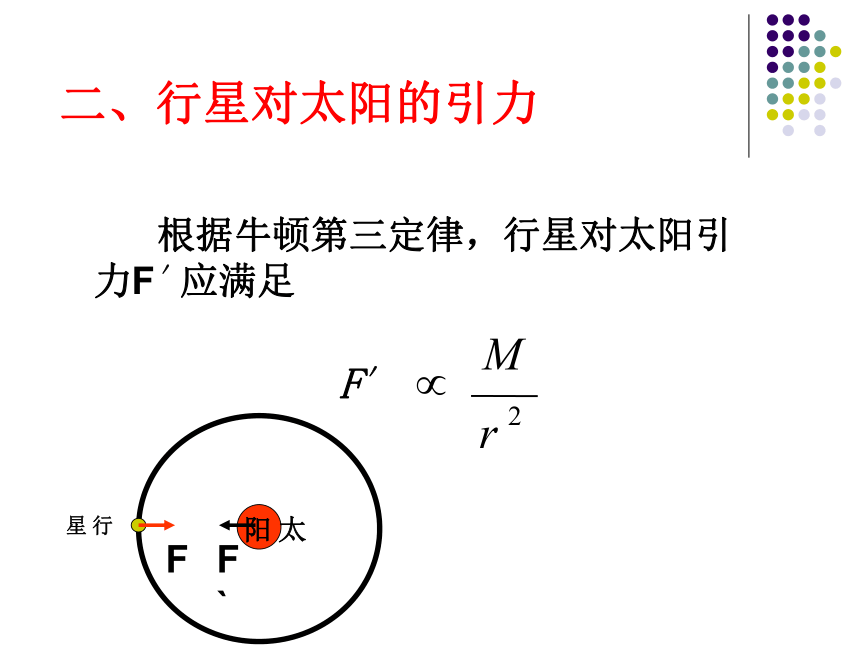
二、行星对太阳的引力
根据牛顿第三定律,行星对太阳引力F'应满足
2
r
M
F'
?
三、太阳与行星间的引力
合二为一:
注:G是比例系数,与太阳、行星的质量无关
写成等式就是:
方向:沿着太阳和行星的连线
此既为太阳与行星间的引力大小
行星绕太阳运动遵守这个规律,那么在其他地方是否适用这个规律呢?
请同学们计算月球的向心加速度,证明结果是否正确。
如果我们已知地球质量为6.0×1024kg.地球半径为6.4×106m,地球到月球距离是地球半径的60倍,请同学们试计算一下月球绕地球的向心加速度是多大?
四、万有引力定律
1、内容:
自然界中任何两个物体都是相互吸引的,引力的大小跟这两个物体的质量的乘积成正比,跟它们的距离的二次方成反比。
2、表达式:
其中G是一个引力常量。
(1)单位:N m2/kg2
(2)标准值:G=6.67259 x10-11N m2/kg2
常用值:G=6.67 x10-11 N m2/kg2
(3) 注意:与重力的符号区别开来
对于距离的确定大致可以分为两种情况:
a.若可以看做质点,则为两质点间距.
b.对于不能视为质点,而质量分布均匀的球体,应是两球心间距.
例题1如图所示,r虽大于两球的半径,但两球的半径不能忽略,而球的质量分布均匀,大小分别为m1与m2,则两球间万有引力的大小为( )
A、
B、
C、
D、
答案:D
◆ 我们人与人之间也一样存在万有引力,可是为什么我们感受不到呢?
假设质量均为60千克的两位同学,相距1米,他们之间的相互作用的万有引力多大?
F=Gm1m2/r2 =6.67×10-11×60×60/12 =2.4×10-7(N)
2.4×10-7N是一粒芝麻重的几千分之一,这么小的力人根本无法察觉到。
◆ 那么太阳与地球之间的万有引力又是多大呢?
已知:太阳的质量为M=2.0×1030kg,地球质量为m=5.8×1025kg,日地之间的距离为R=1.5×1011km
F=GMm/R2
=6.67×10-11×2.0×1030×6.0×1024/(1.5×1011)2
=3.5×1022(N)
3.5×1022N非常大,能够拉断直径为90km的钢柱。
而太阳对质量为50kg的人,引力很小,不到0.3N。当然我们感受不到太阳的引力。
五、引力常量的测量——扭秤实验
(1)实验原理: 科学方法——放大法
卡文迪许
卡文迪许实验室
(2)实验数据
G值为6.67×10-11 Nm2/kg2
(3)卡文迪许扭称实验的意义
①证明了万有引力的存在,使万有引力定律进入了真正实用的时代;
②开创了微小量测量的先河,使科学放大思想得到推广;
1、判断题:
A.行星绕太阳的椭圆轨道可以近似的看作圆形轨道,其向心力来源于太阳对行星的引力 ( )
B.太阳对行星的引力大于行星对太阳的引力,所以行星绕太阳运转而不是太阳绕行星运转( )
练一练:
对
错
2.关于地球和太阳,下列说法正确
的是( ? ) A.地球对太阳的引力比太阳对地球的引力小; B.地球绕太阳运转的向心力来源于太阳对地球的引力; C.太阳对地球的作用力有引力和向心力; D.在地球对太阳的引力作用下,太阳绕地球做圆周运动。
B
3.对于太阳对行星的引力表达式
下面说法正确的是(????) A.公式中G常量,与太阳和行星均无关; B.公式中G由太阳与行星间的距离,作用力和质量决定; C.M和m受到的引力总是大小相等,方向相反,是一对平衡力; D.M和m受到的引力总是大小相等,方向相反,是作用力和反作用力。
AD
3、要使两物体间的万有引力减小到原来的1/4,下列办法可采用的是( )
A.使两物体的质量各减小一半,距离不变
B.使其中一个物体的质量减小到原来的1/4,距离不变
C.使两物体间的距离增为原来的2倍,质量不变
D.使两物体间的距离和质量都减为原来的1/4
ABC
想一想:
如果要验证太阳与行星间的引力规律是否适用于行星与它的卫星,我们需要观测这些卫星运动的哪些数据?观测前你对这些数据的规律有什么假设?
小 结
1、太阳对行星的引力:太阳对不同行星的引力,与行星的质量m成正比,与太阳到行星间的距离r的二次方成反比
2、行星对太阳的引力:与太阳的质量M成正比,与行星到太阳的距离r的二次方成反比
3、太阳与行星间的引力:与太阳的质量M、行星的质量m成正比,与两者距离的二次方成反比
(1) G是比例系数,与行星、太阳均无关
(2)引力的方向沿太阳和行星的连线
太阳与行星间的引力
注意:k值与中心天体有关,而与环绕天体无关。
回顾:
开普勒行星运动定律
即:
思考:是什么原因使行星绕太阳运动呢?
猜想的逻辑顺序:
曲线运动—变速运动—加速度—合外力—引力
行星的运动是受到了来自太阳的类似于磁力的作用 ,与距离成反比。
行星的运动是太阳吸引的缘故,并且力的大小与到太阳距离的平方成反比。
在行星的周围有旋转的物质(以太)作用在行星上,使得行星绕太阳运动。
一切物体都有合并的趋势。
科学足迹
科学足迹
牛顿 (1643—1727)
英国著名的物理学家
当年牛顿在前人研究的基础上,也经过类似同学这样的思考,并凭借其超凡的数学能力和坚定的信念,深入研究,最终发现了万有引力定律。
牛顿在1676年给友人的信中写道:
如果说我看的比别人更远,那是因为我站在巨人的肩膀上。
猜想:引力大小跟什么有关?
追寻牛顿的足迹
讨论验证思路:
由运动情况----加速度----受力情况
一、太阳对行星的引力
1、设行星的质量为m,速度为v,行星到太阳的距离为r,则行星绕太阳做匀速圆周运动的向心力为多少?
代入
由
2、天文观测难以直接得到行星的速度v,但可以得到行星的公转周期T
得到:
3、根据开普勒第三定律:
即
得
代入
4、太阳对行星的引力 :
即:
这表明:太阳对不同行星的引力,与行星的质量成正比,与行星和太阳间的距离的二次方成反比。
二、行星对太阳的引力
根据牛顿第三定律,行星对太阳引力F'应满足
2
r
M
F'
?
三、太阳与行星间的引力
合二为一:
注:G是比例系数,与太阳、行星的质量无关
写成等式就是:
方向:沿着太阳和行星的连线
此既为太阳与行星间的引力大小
行星绕太阳运动遵守这个规律,那么在其他地方是否适用这个规律呢?
请同学们计算月球的向心加速度,证明结果是否正确。
如果我们已知地球质量为6.0×1024kg.地球半径为6.4×106m,地球到月球距离是地球半径的60倍,请同学们试计算一下月球绕地球的向心加速度是多大?
四、万有引力定律
1、内容:
自然界中任何两个物体都是相互吸引的,引力的大小跟这两个物体的质量的乘积成正比,跟它们的距离的二次方成反比。
2、表达式:
其中G是一个引力常量。
(1)单位:N m2/kg2
(2)标准值:G=6.67259 x10-11N m2/kg2
常用值:G=6.67 x10-11 N m2/kg2
(3) 注意:与重力的符号区别开来
对于距离的确定大致可以分为两种情况:
a.若可以看做质点,则为两质点间距.
b.对于不能视为质点,而质量分布均匀的球体,应是两球心间距.
例题1如图所示,r虽大于两球的半径,但两球的半径不能忽略,而球的质量分布均匀,大小分别为m1与m2,则两球间万有引力的大小为( )
A、
B、
C、
D、
答案:D
◆ 我们人与人之间也一样存在万有引力,可是为什么我们感受不到呢?
假设质量均为60千克的两位同学,相距1米,他们之间的相互作用的万有引力多大?
F=Gm1m2/r2 =6.67×10-11×60×60/12 =2.4×10-7(N)
2.4×10-7N是一粒芝麻重的几千分之一,这么小的力人根本无法察觉到。
◆ 那么太阳与地球之间的万有引力又是多大呢?
已知:太阳的质量为M=2.0×1030kg,地球质量为m=5.8×1025kg,日地之间的距离为R=1.5×1011km
F=GMm/R2
=6.67×10-11×2.0×1030×6.0×1024/(1.5×1011)2
=3.5×1022(N)
3.5×1022N非常大,能够拉断直径为90km的钢柱。
而太阳对质量为50kg的人,引力很小,不到0.3N。当然我们感受不到太阳的引力。
五、引力常量的测量——扭秤实验
(1)实验原理: 科学方法——放大法
卡文迪许
卡文迪许实验室
(2)实验数据
G值为6.67×10-11 Nm2/kg2
(3)卡文迪许扭称实验的意义
①证明了万有引力的存在,使万有引力定律进入了真正实用的时代;
②开创了微小量测量的先河,使科学放大思想得到推广;
1、判断题:
A.行星绕太阳的椭圆轨道可以近似的看作圆形轨道,其向心力来源于太阳对行星的引力 ( )
B.太阳对行星的引力大于行星对太阳的引力,所以行星绕太阳运转而不是太阳绕行星运转( )
练一练:
对
错
2.关于地球和太阳,下列说法正确
的是( ? ) A.地球对太阳的引力比太阳对地球的引力小; B.地球绕太阳运转的向心力来源于太阳对地球的引力; C.太阳对地球的作用力有引力和向心力; D.在地球对太阳的引力作用下,太阳绕地球做圆周运动。
B
3.对于太阳对行星的引力表达式
下面说法正确的是(????) A.公式中G常量,与太阳和行星均无关; B.公式中G由太阳与行星间的距离,作用力和质量决定; C.M和m受到的引力总是大小相等,方向相反,是一对平衡力; D.M和m受到的引力总是大小相等,方向相反,是作用力和反作用力。
AD
3、要使两物体间的万有引力减小到原来的1/4,下列办法可采用的是( )
A.使两物体的质量各减小一半,距离不变
B.使其中一个物体的质量减小到原来的1/4,距离不变
C.使两物体间的距离增为原来的2倍,质量不变
D.使两物体间的距离和质量都减为原来的1/4
ABC
想一想:
如果要验证太阳与行星间的引力规律是否适用于行星与它的卫星,我们需要观测这些卫星运动的哪些数据?观测前你对这些数据的规律有什么假设?
小 结
1、太阳对行星的引力:太阳对不同行星的引力,与行星的质量m成正比,与太阳到行星间的距离r的二次方成反比
2、行星对太阳的引力:与太阳的质量M成正比,与行星到太阳的距离r的二次方成反比
3、太阳与行星间的引力:与太阳的质量M、行星的质量m成正比,与两者距离的二次方成反比
(1) G是比例系数,与行星、太阳均无关
(2)引力的方向沿太阳和行星的连线
