沪科版九年级下册数学:第二十六章 概率初步小结·评价(3) 课件(共21张PPT)
文档属性
| 名称 | 沪科版九年级下册数学:第二十六章 概率初步小结·评价(3) 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-03-30 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
第26章 概率初步
小结与复习
沪科版数学九年级下册
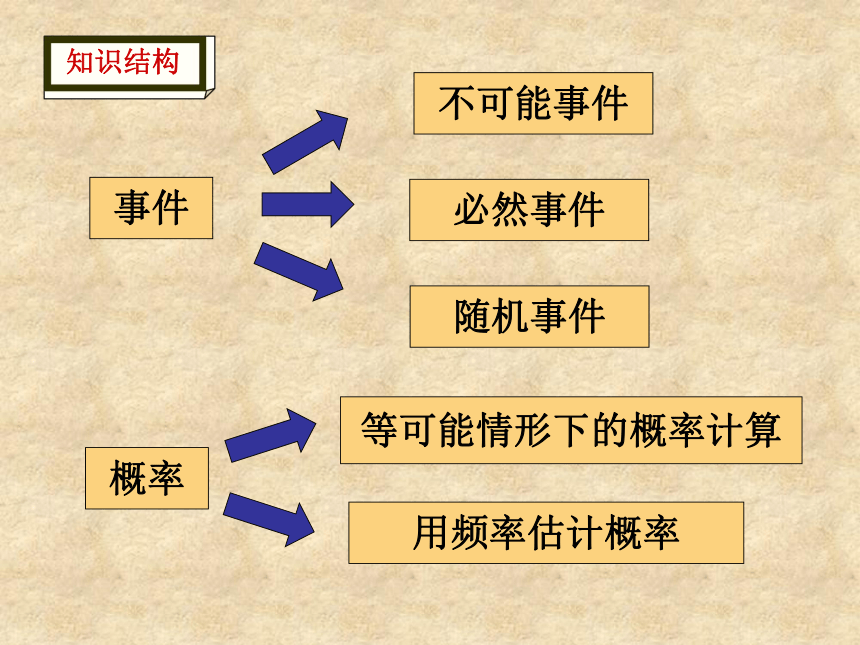
事件
用频率估计概率
等可能情形下的概率计算
随机事件
必然事件
不可能事件
概率
知识结构
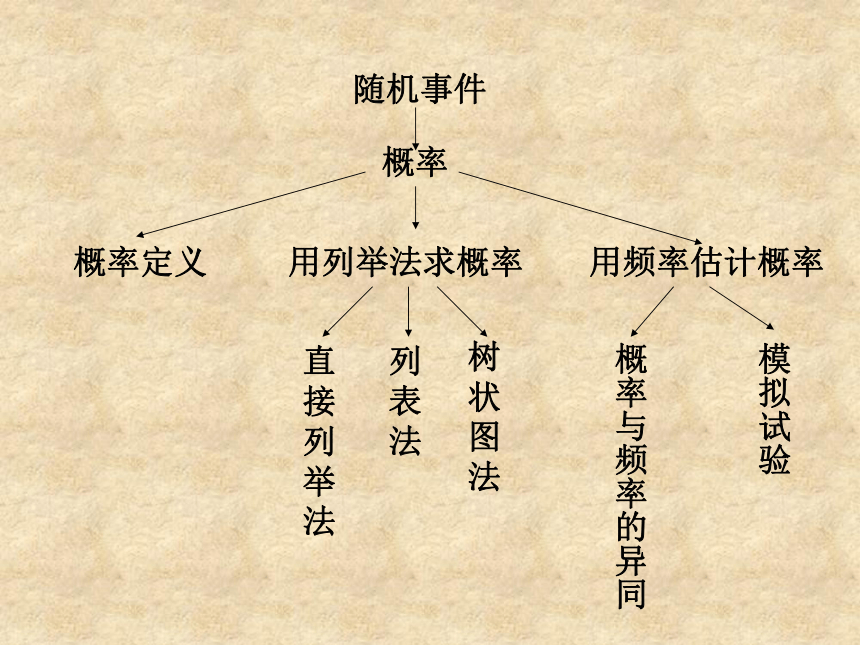
随机事件
概率
概率定义
用频率估计概率
用列举法求概率
列表法
树状图法
概率与频率的异同
模拟试验
直接列举法
在一定条件下必然要发生的事件,叫做必然事件。
在一定条件下不可能发生的事件,叫做不可能事件。
在一定条件下可能发生也可能不发生的事件,叫做随机事件。
1.随机事件
事件发生的概率与事件发生的频率有什么联系?
一般地,在大量重复进行同一试验时,事件A发生的频率m/n稳定在某个常数 p 的附近,那么这个常数就叫做事件A的概率,
记作 P(A)=P.
2.概 率
如何用列举法求概率?
1).当事件要经过一步完成时,用直接列举法列出所有可能情况。
2).当事件要经过两步完成时,用列表法,列举出所有可能情况。
3).当事件要经过三步以上完成时,用树状图法,列举所有可能情况。
当试验的所有可能结果不是有限个,或各种可能结果发生的可能性不相等时,常常是通过统计频率来估计概率,即在同样条件下,用大量重复试验所得到的随机事件发生的频率的稳定值来估计这个事件发生的概率。
用频率估计概率的一般做法
3.频率估计概率
例1 如图,把三张卡片放在盒子里搅匀,任取两张,拼成菱形或房子,求拼成菱形和拼成房子的概率各是多少.
经典例题
例2 如图所示的图案中,黑白两色的直角三角形都全等.将它作为一个游戏盘,游戏规则是:按一定距离向盘中投镖一次,扎在黑色区域为甲胜,扎在白色区域为乙胜.你认为这个游戏公平吗?为什么?
答:我认为这个游戏公平。因为
P(扎在黑色区域)=P(扎在白色区域)= 1/2.
例3 下列事件一定为必然事件的是( ).
A.重庆人都爱吃火锅
B.某校随机检查20名学生的血型,其中必
有A型
C.两直线平行,同位角相等
D.在数轴上,到原点距离相等的点所表示
的数一定相等
C
例4 根据你的经验,分别写出下列事件发生的机会:
A.在一个不透明的袋中装有红球3个、白球2个、黑
球1个,每种球除颜色外其余都相同,是摇匀后随机
从袋中取出一个球,取到红球的机会 ;
B.掷一枚普通正方形骰子,出现的点数为7的机会
是 ;
0
C.掷两枚普通硬币,出现两个正面的机会是 .
例5 某中学九年级有6个班,要从中选出2个班代表学校参加某项活动,1班必须参加,另外再从2至6班选出一个班.4班有学生建议用如下的方法:从装有编号为1,2,3的三个白球的袋子中摸出一个球,再从装有编号为1,2,3的三个红球的袋子中摸出一个球(两袋中球的大小、形状与质量完全一样),摸出的两个球上的数字和是几,就选几班,你认为这种方法公平吗?请说明理由.
解:可能出现的所有结果如下:
第2次
第1次 1 2 3
1
2
3
从表中可知:
P(数字之和为2)=1/9,
P(数字之和为3)=2/9,
P(数字之和为4)=1/3,
P(数字之和为5)=2/9,
P(数字之和为6)=1/9.
其中2班,6班被选出的概率只有1/9,而4班被选出的概率是1/3,所以这种方法不公平.
例6 请你依据图框中的寻宝游戏
规则,探究“寻宝游戏”的奥秘:
寻宝游戏:如图,有三间房,每间房内放有两个柜子,仅有一件宝物藏在某个柜子中,游戏规则:只允许进入三个房间中的一个房间并打开其中一个柜子即为一次游戏结束.找到宝物为游戏胜出,否则为游戏失败.
(1)用树状图表示出所有可能的寻宝情况;
(2)求在寻宝游戏中胜出的概率.
C
2.(抢答题)如图所示,如果小明将镖随意投中正方形木板,那么镖落在阴影部分的概率为( ).
1.(抢答题)乘火车从A站出发,沿途经过3个车站方可到达B站,那么在A、B 两站之间需要安排 种不同的车票.
20
3.下列事件中哪些是必然事件? (1)平移后的图形与原来图形对应线段相等
(2)任意一个五边形外角和等于5400. (3)若3>2,则3c>2c (4)从装有两个红球和一个白球的口袋中,摸出两个球一定有一个红球。 (5)在一个等式两边同时除以同一个数,结果仍是等式
4.将分别标有数字1,2,3的三张卡片洗匀后,背面朝上放在桌面上.
(1)随机地抽取一张,求P(奇数);
(2)随机地抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,能组成哪些两位数?恰好是“32”的概率为多少?
5.你能说出几个与必然事件、随机事件、不可能事件相联系的成语吗?
如:必然事件:种瓜得瓜,种豆得豆,
黑白分明。
6.在一个不透明的口袋中装有除颜色外其余都相同的1个红球,2个黄球,如果每一次先从袋中摸出1个球后不再放回,第二次再从袋中摸出1个球,那么两次都摸到黄球的概率是多少?
随机事件:海市蜃楼,守株待兔。
不可能事件:海枯石烂,画饼充饥,拔苗助长。
7.深夜,发生了一起出租车交通肇事逃逸事件.该地区有两种出租车—绿色出租车和蓝色出租车,它们分别占整个地区出租车的85%和15%.据现场目击证人说,肇事出租车为蓝色.警方对证人的辨别能力做了测试,测得他的正确辨别率是80%.警方认为蓝色出租车涉嫌肇事的可能性大,你同意这一观点吗?请你帮助交警判断哪种出租车肇事的可能性大,并说明理由.
解:绿色出租车涉嫌肇事的可能性大些.假设该地区有a辆出租车,则有0.85a辆绿色车,0.15a辆蓝色车.
证人可将0.85a×0.2=0.17a辆绿色车看成蓝色车,将0.15a×0.8=0.12a辆蓝色车看准.所以证人可能将0.29a辆车说成蓝色车.
证人所说的蓝色肇事车,有0.17a÷0.29a≈58.62%的可能是绿色车,有0.12a÷0.29a≈41.38%的可能是蓝色车.
这节课你收获了什么?
还有什么与大家交流的?
知识梳理
作业:资料90页
第26章 概率初步
小结与复习
沪科版数学九年级下册
事件
用频率估计概率
等可能情形下的概率计算
随机事件
必然事件
不可能事件
概率
知识结构
随机事件
概率
概率定义
用频率估计概率
用列举法求概率
列表法
树状图法
概率与频率的异同
模拟试验
直接列举法
在一定条件下必然要发生的事件,叫做必然事件。
在一定条件下不可能发生的事件,叫做不可能事件。
在一定条件下可能发生也可能不发生的事件,叫做随机事件。
1.随机事件
事件发生的概率与事件发生的频率有什么联系?
一般地,在大量重复进行同一试验时,事件A发生的频率m/n稳定在某个常数 p 的附近,那么这个常数就叫做事件A的概率,
记作 P(A)=P.
2.概 率
如何用列举法求概率?
1).当事件要经过一步完成时,用直接列举法列出所有可能情况。
2).当事件要经过两步完成时,用列表法,列举出所有可能情况。
3).当事件要经过三步以上完成时,用树状图法,列举所有可能情况。
当试验的所有可能结果不是有限个,或各种可能结果发生的可能性不相等时,常常是通过统计频率来估计概率,即在同样条件下,用大量重复试验所得到的随机事件发生的频率的稳定值来估计这个事件发生的概率。
用频率估计概率的一般做法
3.频率估计概率
例1 如图,把三张卡片放在盒子里搅匀,任取两张,拼成菱形或房子,求拼成菱形和拼成房子的概率各是多少.
经典例题
例2 如图所示的图案中,黑白两色的直角三角形都全等.将它作为一个游戏盘,游戏规则是:按一定距离向盘中投镖一次,扎在黑色区域为甲胜,扎在白色区域为乙胜.你认为这个游戏公平吗?为什么?
答:我认为这个游戏公平。因为
P(扎在黑色区域)=P(扎在白色区域)= 1/2.
例3 下列事件一定为必然事件的是( ).
A.重庆人都爱吃火锅
B.某校随机检查20名学生的血型,其中必
有A型
C.两直线平行,同位角相等
D.在数轴上,到原点距离相等的点所表示
的数一定相等
C
例4 根据你的经验,分别写出下列事件发生的机会:
A.在一个不透明的袋中装有红球3个、白球2个、黑
球1个,每种球除颜色外其余都相同,是摇匀后随机
从袋中取出一个球,取到红球的机会 ;
B.掷一枚普通正方形骰子,出现的点数为7的机会
是 ;
0
C.掷两枚普通硬币,出现两个正面的机会是 .
例5 某中学九年级有6个班,要从中选出2个班代表学校参加某项活动,1班必须参加,另外再从2至6班选出一个班.4班有学生建议用如下的方法:从装有编号为1,2,3的三个白球的袋子中摸出一个球,再从装有编号为1,2,3的三个红球的袋子中摸出一个球(两袋中球的大小、形状与质量完全一样),摸出的两个球上的数字和是几,就选几班,你认为这种方法公平吗?请说明理由.
解:可能出现的所有结果如下:
第2次
第1次 1 2 3
1
2
3
从表中可知:
P(数字之和为2)=1/9,
P(数字之和为3)=2/9,
P(数字之和为4)=1/3,
P(数字之和为5)=2/9,
P(数字之和为6)=1/9.
其中2班,6班被选出的概率只有1/9,而4班被选出的概率是1/3,所以这种方法不公平.
例6 请你依据图框中的寻宝游戏
规则,探究“寻宝游戏”的奥秘:
寻宝游戏:如图,有三间房,每间房内放有两个柜子,仅有一件宝物藏在某个柜子中,游戏规则:只允许进入三个房间中的一个房间并打开其中一个柜子即为一次游戏结束.找到宝物为游戏胜出,否则为游戏失败.
(1)用树状图表示出所有可能的寻宝情况;
(2)求在寻宝游戏中胜出的概率.
C
2.(抢答题)如图所示,如果小明将镖随意投中正方形木板,那么镖落在阴影部分的概率为( ).
1.(抢答题)乘火车从A站出发,沿途经过3个车站方可到达B站,那么在A、B 两站之间需要安排 种不同的车票.
20
3.下列事件中哪些是必然事件? (1)平移后的图形与原来图形对应线段相等
(2)任意一个五边形外角和等于5400. (3)若3>2,则3c>2c (4)从装有两个红球和一个白球的口袋中,摸出两个球一定有一个红球。 (5)在一个等式两边同时除以同一个数,结果仍是等式
4.将分别标有数字1,2,3的三张卡片洗匀后,背面朝上放在桌面上.
(1)随机地抽取一张,求P(奇数);
(2)随机地抽取一张作为十位上的数字(不放回),再抽取一张作为个位上的数字,能组成哪些两位数?恰好是“32”的概率为多少?
5.你能说出几个与必然事件、随机事件、不可能事件相联系的成语吗?
如:必然事件:种瓜得瓜,种豆得豆,
黑白分明。
6.在一个不透明的口袋中装有除颜色外其余都相同的1个红球,2个黄球,如果每一次先从袋中摸出1个球后不再放回,第二次再从袋中摸出1个球,那么两次都摸到黄球的概率是多少?
随机事件:海市蜃楼,守株待兔。
不可能事件:海枯石烂,画饼充饥,拔苗助长。
7.深夜,发生了一起出租车交通肇事逃逸事件.该地区有两种出租车—绿色出租车和蓝色出租车,它们分别占整个地区出租车的85%和15%.据现场目击证人说,肇事出租车为蓝色.警方对证人的辨别能力做了测试,测得他的正确辨别率是80%.警方认为蓝色出租车涉嫌肇事的可能性大,你同意这一观点吗?请你帮助交警判断哪种出租车肇事的可能性大,并说明理由.
解:绿色出租车涉嫌肇事的可能性大些.假设该地区有a辆出租车,则有0.85a辆绿色车,0.15a辆蓝色车.
证人可将0.85a×0.2=0.17a辆绿色车看成蓝色车,将0.15a×0.8=0.12a辆蓝色车看准.所以证人可能将0.29a辆车说成蓝色车.
证人所说的蓝色肇事车,有0.17a÷0.29a≈58.62%的可能是绿色车,有0.12a÷0.29a≈41.38%的可能是蓝色车.
这节课你收获了什么?
还有什么与大家交流的?
知识梳理
作业:资料90页
