18.2.1 矩形同步测试题2(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版2019-2020学年八年级下学期
18.2.1矩形
(时间60分钟 总分100分)
一、选择题(每小题5分,共30分)
1.下列命题原命题与逆命题都是真命题的是( )
A.矩形的对角线相等
B.对角线互相平分且相等的四边形是矩形
C.矩形有一个内角是直角
D.对角线互相垂直且平分的四边形是矩形
2.如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
A.AB||DC B.AC=BD C.ACBD D.AB=DC
3.如图,在矩形ABCD中,若AC=2AB,则AOB的大小是( )
A. B. C. D.
4.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B处,若AE-2,DE-6,A. 12 B. 24 C. D.
5.如图,矩形ABCD的对角线AC与BD交于点0,过点作BD的垂线分别交AD,BC于E,F两点.若,则FC的长度为( )
A.1 B.2 C. D.
6.如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠使点C与点A重合,则折痕EF的长为( )
A.6 B.12 C. D.
二、填空题(每小题5分,共20分)
7.如图所示,已知矩形ABCD周长为24cm,对角线交于点0,OEDC于点E,OFAD于点F,OF-OE=2cm,则AB=________,BC=_________
8.如图1所示,矩形ABCD中的两条对角线相交于点O,∠AOD=120°,AB=4cm,则矩形的对角线的长为_____.
9.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,若AB=6cm,BC=8cm,则AEF的周长__________cm
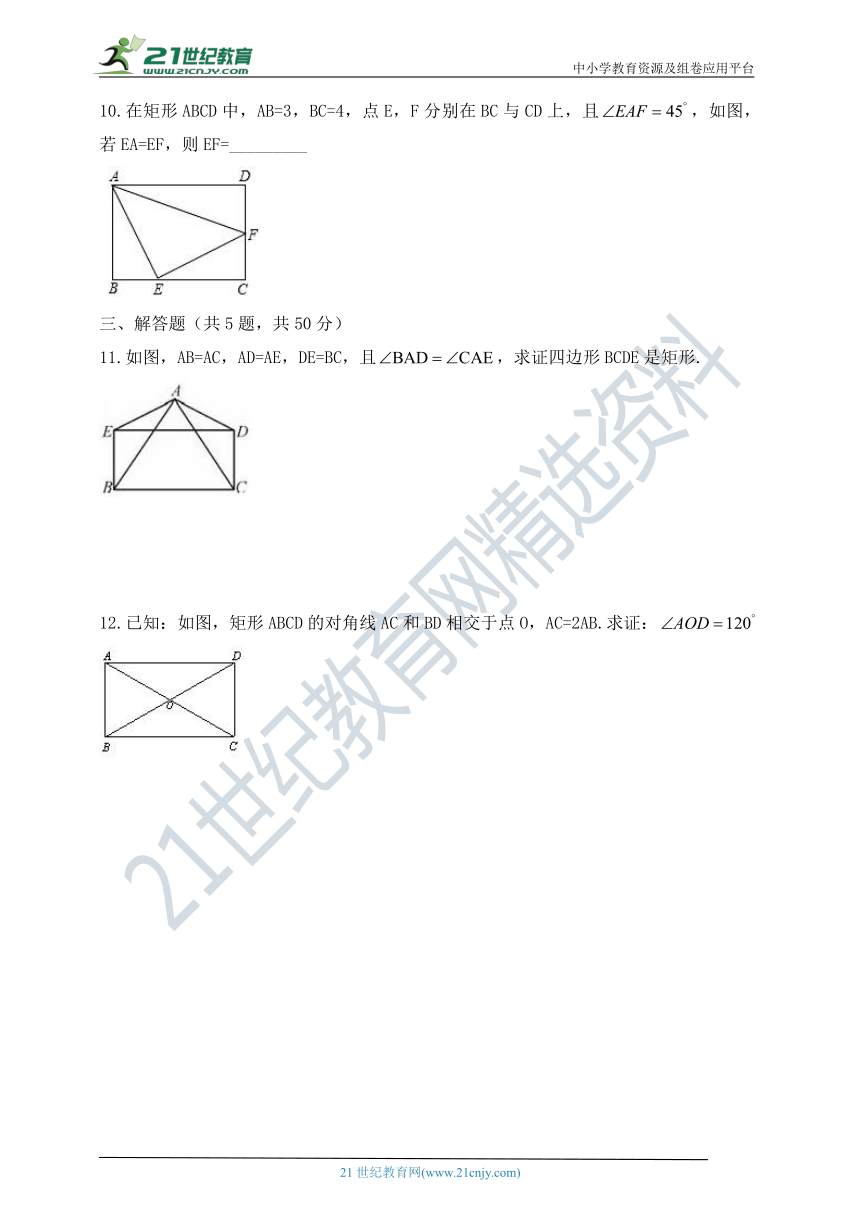
10.在矩形ABCD中,AB=3,BC=4,点E,F分别在BC与CD上,且,如图,若EA=EF,则EF=_________
三、解答题(共5题,共50分)
11.如图,AB=AC,AD=AE,DE=BC,且,求证四边形BCDE是矩形.
12.已知:如图,矩形ABCD的对角线AC和BD相交于点O,AC=2AB.求证:
13.如图,在矩形ABCD中,AC,BD相交于点0,AE平分BAD,交BC于点E,若,求BOE的度数.
14.已知:如图,ABCD的四个内角的角平分线分别交于E,F,G,H.试说明四边形EFGH为矩形.
15.如图,四边形ABCD是矩形,对角线AC,BD相交于点0,BE||AC交DC的延长线于点E.
(1)求证:BD = BE;
(2)若,求四边形ABED的面积
答案
1.【解析】A、矩形的对角线相等,逆命题是对角线相等的四边形是矩形,错误;B、对角线互相平分且相等的四边形是矩形,逆命题是矩形的对角线互相平分且相等,正确;C、矩形有一个内角是直角,逆命题是有一个内角是直角的四边形是矩形,错误;D、对角线互相垂直且平分的四边形是矩形,错误。故选B。
2.【解析】C
3.【解析】是正三角形,所以AOB的大小是60,故选C
4.【解析】如图,连接BE,在矩形ABCD中
把矩形ABCD沿EF翻折点B恰好落在AD边的B'处,
,在RtABE中
,
所以矩形ABCD的面积,故选D。
5.【解析】四边形ABCD是矩形,
,故选A。
6.【解析】设BE=x,则CE=BC-BE=16-x,因为沿EF翻折后点C与点A重合,所以AE=CE=16-x,在RtABE中,,即,解得x=6,
由翻折的性质得,AEF=CEF,矩形ABCD的对边AD||BC,
,,过 E作EHAD于H,则四边形ABEH是矩形,
,,,在RtEFH中,EF=
==4,故选D。
7.【解析】
因为OF-OE-2,所以CD-AD=4
因为CD+AD=12
所以AB=CD=8,BC=AD=4
8.【解析】8
9.【解析】在RtABC中,
因为点E,F分别是AO,AD的中点,
因为E,F分别是AO,AD的中点
所以EF是AOD的中位线
所以AEF的周长
故答案为:9
10.【解析】
所以AEF等直三形,
又因为在AEF中,
又
,
在ABE和ECF中
在RtCEF中,由勾股定理得:
故答案为
11.【解析】
又
所以四边形BCDE是平行四边形.
连接BD,CE.
所以四边形BCDE是矩形
12.【解析】因为矩形ABCD,,在RtABC中,AC=2AB,
,,,,
,
13.【解析】因为四边形ABCD是矩形,
因为AE是BAD的平分线
所以AOB等边三角形,
在RtABE中,
又
14.【解析】因为四边形ABCD是平行四边形
又ABCD的四个内角的角平分线分别交于E,F,G,H.
同理可证
所以四边形EFGH为矩形.
15.【解析】(1)证明:因为四边形ABCD是矩形
又
所以四边形ABEC是平行四边形.
(2)因为四边形ABCD是矩形,
所以ABO是等边三角形,即AB=OB=4,于是AB=DC=CE=4.
在RtDBC中,DC=4,BD=8,
因为AB||DE,AD与BE不平行,
所以四边形ABED是梯形,且BC为梯形的高
所以四边形ABED的面积
_21?????????è?????(www.21cnjy.com)_
人教版2019-2020学年八年级下学期
18.2.1矩形
(时间60分钟 总分100分)
一、选择题(每小题5分,共30分)
1.下列命题原命题与逆命题都是真命题的是( )
A.矩形的对角线相等
B.对角线互相平分且相等的四边形是矩形
C.矩形有一个内角是直角
D.对角线互相垂直且平分的四边形是矩形
2.如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
A.AB||DC B.AC=BD C.ACBD D.AB=DC
3.如图,在矩形ABCD中,若AC=2AB,则AOB的大小是( )
A. B. C. D.
4.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B处,若AE-2,DE-6,
5.如图,矩形ABCD的对角线AC与BD交于点0,过点作BD的垂线分别交AD,BC于E,F两点.若,则FC的长度为( )
A.1 B.2 C. D.
6.如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠使点C与点A重合,则折痕EF的长为( )
A.6 B.12 C. D.
二、填空题(每小题5分,共20分)
7.如图所示,已知矩形ABCD周长为24cm,对角线交于点0,OEDC于点E,OFAD于点F,OF-OE=2cm,则AB=________,BC=_________
8.如图1所示,矩形ABCD中的两条对角线相交于点O,∠AOD=120°,AB=4cm,则矩形的对角线的长为_____.
9.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,若AB=6cm,BC=8cm,则AEF的周长__________cm
10.在矩形ABCD中,AB=3,BC=4,点E,F分别在BC与CD上,且,如图,若EA=EF,则EF=_________
三、解答题(共5题,共50分)
11.如图,AB=AC,AD=AE,DE=BC,且,求证四边形BCDE是矩形.
12.已知:如图,矩形ABCD的对角线AC和BD相交于点O,AC=2AB.求证:
13.如图,在矩形ABCD中,AC,BD相交于点0,AE平分BAD,交BC于点E,若,求BOE的度数.
14.已知:如图,ABCD的四个内角的角平分线分别交于E,F,G,H.试说明四边形EFGH为矩形.
15.如图,四边形ABCD是矩形,对角线AC,BD相交于点0,BE||AC交DC的延长线于点E.
(1)求证:BD = BE;
(2)若,求四边形ABED的面积
答案
1.【解析】A、矩形的对角线相等,逆命题是对角线相等的四边形是矩形,错误;B、对角线互相平分且相等的四边形是矩形,逆命题是矩形的对角线互相平分且相等,正确;C、矩形有一个内角是直角,逆命题是有一个内角是直角的四边形是矩形,错误;D、对角线互相垂直且平分的四边形是矩形,错误。故选B。
2.【解析】C
3.【解析】是正三角形,所以AOB的大小是60,故选C
4.【解析】如图,连接BE,在矩形ABCD中
把矩形ABCD沿EF翻折点B恰好落在AD边的B'处,
,在RtABE中
,
所以矩形ABCD的面积,故选D。
5.【解析】四边形ABCD是矩形,
,故选A。
6.【解析】设BE=x,则CE=BC-BE=16-x,因为沿EF翻折后点C与点A重合,所以AE=CE=16-x,在RtABE中,,即,解得x=6,
由翻折的性质得,AEF=CEF,矩形ABCD的对边AD||BC,
,,过 E作EHAD于H,则四边形ABEH是矩形,
,,,在RtEFH中,EF=
==4,故选D。
7.【解析】
因为OF-OE-2,所以CD-AD=4
因为CD+AD=12
所以AB=CD=8,BC=AD=4
8.【解析】8
9.【解析】在RtABC中,
因为点E,F分别是AO,AD的中点,
因为E,F分别是AO,AD的中点
所以EF是AOD的中位线
所以AEF的周长
故答案为:9
10.【解析】
所以AEF等直三形,
又因为在AEF中,
又
,
在ABE和ECF中
在RtCEF中,由勾股定理得:
故答案为
11.【解析】
又
所以四边形BCDE是平行四边形.
连接BD,CE.
所以四边形BCDE是矩形
12.【解析】因为矩形ABCD,,在RtABC中,AC=2AB,
,,,,
,
13.【解析】因为四边形ABCD是矩形,
因为AE是BAD的平分线
所以AOB等边三角形,
在RtABE中,
又
14.【解析】因为四边形ABCD是平行四边形
又ABCD的四个内角的角平分线分别交于E,F,G,H.
同理可证
所以四边形EFGH为矩形.
15.【解析】(1)证明:因为四边形ABCD是矩形
又
所以四边形ABEC是平行四边形.
(2)因为四边形ABCD是矩形,
所以ABO是等边三角形,即AB=OB=4,于是AB=DC=CE=4.
在RtDBC中,DC=4,BD=8,
因为AB||DE,AD与BE不平行,
所以四边形ABED是梯形,且BC为梯形的高
所以四边形ABED的面积
_21?????????è?????(www.21cnjy.com)_
